Apparatus description

In the e/m apparatus electrons are accelerated through a potential difference V (200 V - 300 V) in a spherical tube filled with helium gas at a low pressure of 10^-2 mm H. 

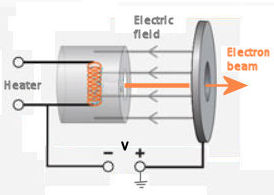In the tube a filament (the cathode) is heated and emits electrons which are accelerated by the potential difference V between the cathode and the anode (ground).  A beam of electrons emerges through a hole in the anode.  A grid can help to focus the electron beam.

The accelerating voltage V determines the kinetic energy and therefore the speed v of the electrons.  The electron beam leaves a visible trail in the tube, because some of the electrons collide with helium atoms.  The atoms are excited and then radiate visible light.

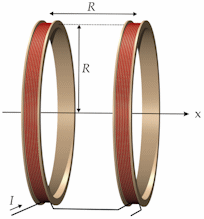A pair of Helmholtz coils produces a nearly uniform magnetic field in the regions of the spherical tube.  Helmholtz coils are two coils with radius R are separated by the same distance R.  When the coils are connected so that the same current flows through both coils in the same direction, the Helmholtz coils produce a region with a nearly uniform magnetic field near the center of the coils.  The Helmholtz coils of the e/m apparatus have a radius and a separation of R = 15 cm.  The magnitude of the magnetic field B produced by these coils is proportional to the current I flowing through the coils.  B =  (7.56*10^-4 T/A) * I.  The direction of B is perpendicular to the plane of the coils.

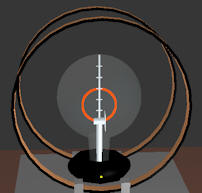The e/m tube has a radius of 7.5 cm.  If the tube has not been rotated, B is perpendicular to the electron beam velocity and deflects the electron beam into a circular path.  The diameter of this circular path can be measured using the calibration marks in the center of the tube, which are equally spaced by 2 cm.  In the picture on the right the diameter of the circular path is 6 cm.

The e/m tube can also be rotated by up to 10^o, allowing the electron beam velocity to make an angle between 0 to 10^o with the magnetic field.  The vector nature of the magnetic force on a moving charged particles can therefore be explored. 

Apparatus controls

• Use the mouse.  Click the table to rotate the view.
• Move the mouse wheel to zoom in and out.
• Click the on/off switch to turn the power supply on and off.  It takes a moment for the filament to heat up and the electron path to become visible.
• Click the current knob (A) and move the mouse horizontally across it to adjust the coil current (0 A - 4 A).
  The magnitude of the magnetic field B in the region of the electron tube is proportional to the coil current I.
  B = (7.56*10^-4 T/A)*I.
  When facing the control panel of the apparatus, the current I flows clockwise through the coils and the magnetic field points from the front side to the back side of the apparatus.
• Click the voltage knob (V) and move the mouse horizontally across it to adjust the voltage (200 V - 300 V).
• Click the black ring holding the tube and move the mouse horizontally across it to rotate the tube up to 10^o in either direction.
• always release the mouse button after an operation.

Analysis of an e/m measurement

The magnetic force F_m acting on a charged particle of charge q moving with velocity v in a magnetic field B is given by the equation

F_m = qv × B. 

If the electron beam velocity is perpendicular to the magnetic field, we have the following equation relating the magnitudes F_m, q, v, and B.

F_m = qvB.

The electron is moving in a circular path of radius r, with the magnetic force being equal to the centripetal force mv²/r.  We therefore have

qvB = mv²/r   or   q/m = v/Br.

We denote the magnitude of the charge q of the electron by e and therefore have e/m = v/Br.
The electrons are accelerated by the accelerating potential V, gaining kinetic energy equal to their charge times the accelerating potential.
Therefore eV = ½mv².
The velocity of the electrons is v = (2eV/m)^½.  I
nserting this expression for v in the equation above and squaring both sides we obtain

e/m = 2V/(Br)²  or  2V = (e/m) (Br)².

The slope of a plot of 2V versus (Br)² is equal to electron charge to mass ration e/m.