Everyday, objects or people collide, sometimes by accident and sometimes on
purpose. In a collision, the momentum of each colliding partner changes in
a very short time interval. Each collision partner receives an impulse.
A momentum change or impulse requires a force. For the
momentum to change by an amount ∆p a
force F must act for a time ∆t such that ∆p
= F∆t. The shorter the collision time, the larger are the
forces acting on the collision partners.
Many safety devices, such as seat belts, airbags, crumple zones, etc, are
standard equipment on modern cars. The purpose of these devices is to
increase the time it takes for a passenger's velocity to change by a
large amount in the event of a collision. In sports, pads are designed to
increase the collision time and therefore reduce the force acting on a player
during a collision which changes the player's momentum by an amount ∆p.
If a pad doubles the collision time, it decreases the force by a factor of 2.
In this laboratory we will investigate the relationship between force,
collision time and impulse, and we will also examine momentum conservation in
elastic and inelastic collisions.
Open a Microsoft Word document to keep a log of your experimental procedures, results and discussions. Address everything that appears in blue font. This log will form the basis of your lab report.
A cart rolls down an inclined track and collides with a wood block at the end of the track. The wood block is padded with another block made of metal, wood, or foam, for four different experimental runs. Since the car is released from rest at the same position on the track every time, its speed when it makes contact with the block is approximately the same every time. An acceleration sensor measures the acceleration as a function of time during the collision and a computer displays the output of the acceleration sensor. The magnitude of the interaction force F is proportional to the acceleration, F = ma. The output of the acceleration sensor under different collision conditions is shown below.
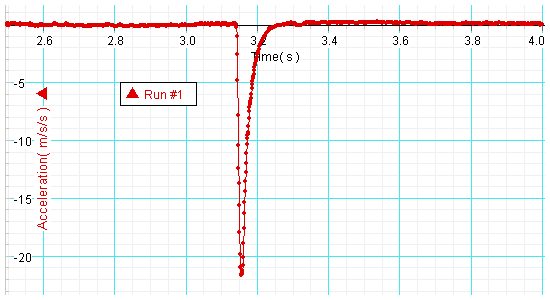
The cart collides with an aluminum block. The magnitude of the maximum measured acceleration is ~22 m/s2. The collision lasts for ~0.09 s


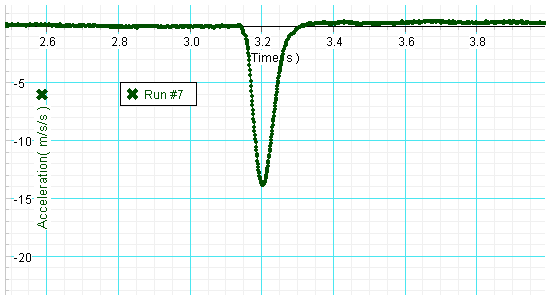
The cart collides with a wood block. The magnitude of the maximum measured acceleration is ~21 m/s2. The collision lasts for ~0.1 s.
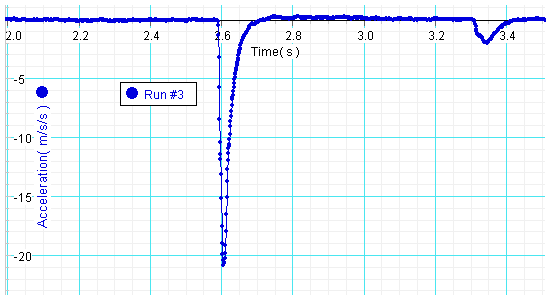

The cart collides with a high-density foam block. The magnitude of the maximum measured acceleration is ~17 m/s2. The collision lasts for ~0.12 s.
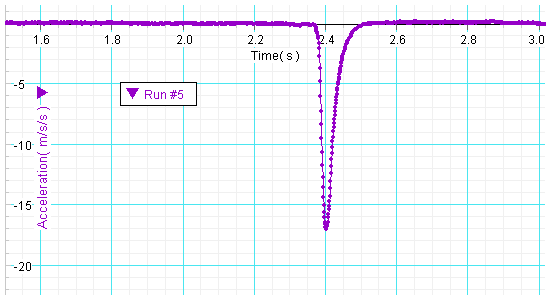

The cart collides with another foam block. This type of foam is used for packing fragile materials for shipping. The magnitude of the maximum measured acceleration is ~14 m/s2. The collision lasts for ~0.15 s.

The mass of the cart with the attached acceleration sensor is 555 g.
Fill in the table below.
| Bumper block | Aluminum | Wood | High-density foam | Low-density foam |
|---|---|---|---|---|
| Maximum force | ||||
| Collision time | ||||
| Impulse Favg*∆t |
In order to estimate the impulse during the collision, you need to find the area under the peak in the acceleration versus time graph (units m/s2 * s = m/s) and then multiply by the mass of the cart.
Place a wide textbook on the floor and stand on it. Then you
jump off the book onto the floor two different times. The first time you
land normally, allowing your knees to bend. The second time you land
stiff-legged, not allowing your knees to bend. Do these jumps feel
different to you? Explain!
You will now investigate elastic and inelastic collisions between two carts on a track. In elastic collisions the carts bounce off each other and in inelastic collisions they stick together. The momentum of an object is the product of its mass and its velocity, p = mv. If external forces acting in the horizontal direction (such as friction) can be ignored in the experiments of this lab, then the sum of the momenta of the two carts prior to a collision should be the same as the sum of the momenta of the carts after the collision. You will explore the implication of momentum conservation under various collision conditions.

Procedure:
Analyze three video clips and fill in the table below.
| before the collision | after the collision | |||||
|---|---|---|---|---|---|---|
| pcart 1 | pcart 2 | ptotal | pcart 1 | pcart 2 | ptotal | |
| Video 1 | ||||||
| Video 2 | ||||||
| Video3 | ||||||
Video 1: An elastic collision
Before the collision cart 1 travels towards the left and cart 2 travels towards the right. During the collision they reverse their directions.
Determine the momentum of each cart and the total momentum of both carts before and after the collision. Enter the values into your table. Make sure that you enter them with the right sign. If friction were completely negligible, the total momentum should not change. With a small amount of friction present its magnitude probably decreases, but only by a small amount.
Video 2: Another elastic collision
In this experiment both carts travel to the left before and after the collision.
Determine the momentum of each cart and the total momentum of both carts before and after the collision. Enter the values into your table. Make sure that you enter them with the right sign.
Video 3: A inelastic collision
Before the collision cart 1 travels towards the left and cart 2 travels towards the right. After the collision they stick together and travel with the same speed towards the left.
Determine the momentum of each cart and the total momentum of both carts before and after the collision. Enter the values into your table. Make sure that you enter them with the right sign.
Discuss your results!
Convert your log into a lab report.
Name:
E-mail address:
Laboratory 7 Report
Save your Word document (your name_lab7.docx), go to Canvas, Assignments, Lab 7, and submit your document.