Units and conversions

Physicist want to predict the outcome of measurements.

The result of every measurement has two parts, a number and a unit.  The number is the answer to "How many?" and the unit is the answer to "Of what?".  Units are standard quantities such as a second, a meter, a mile.  The most widely used units today are those of the international system, abbreviated SI (Systeme International d'Unites).  Examples of SI units are the meter (m) for length, the second (s) for time, and the kilogram (kg) for mass.  The unit of an observable carries information about the dimension of the observable.  If a quantity is measured in meters, than its dimension is length (L), if it is measured in kilogram, than its dimension is mass (M).

SI base units:

• meter (m) for length
• Ampere (A) for electric current
• second (s) for time
• Kelvin (K) for temperature
• kilogram (kg) for mass
• mole (mol) for amount of substance
• candela (cd) for luminous intensity

The 20 SI prefixes used to form decimal multiples and submultiples of SI units are given in Table below.

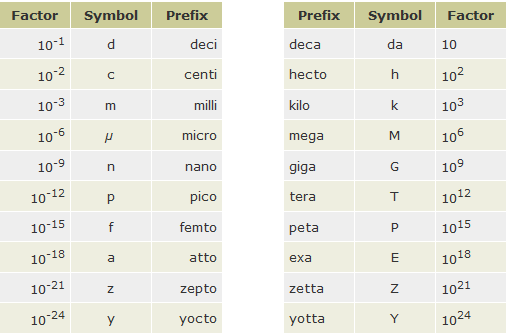
Anything that can be measured can be expressed in some combination of SI base units.  Derived units are common combinations with special names.
Example: kg m/s² = N (Newton) = SI unit of force

If you work problems in SI units, the result will automatically be in SI units.  If the input quantities are given in different units, convert to SI units!

Problem:

The speed of a car is 35 miles/hour.  What is the speed of this car in SI units (m/s)?
Conversions: 1 mile = 1609.3 m, 1 hour = 3600 s.

Solution:

• Reasoning:
  Multiply by the conversion factors in such a way that the unwanted units cancel out.
• Details of the calculation:
  (35 miles/h)*(1 h/3600s)* (1609.3 m/1 mile) = 15.65 m/s.

Problem:

A fire burned an area of 6 square miles.  How many square meters were burned?

Solution:

• Reasoning:
  Multiply by the conversion factors in such a way that the unwanted units cancel out.
• Details of the calculation:
  (6 miles²)*(1609.3 m/mile)² = 1.55*107 m².

Note: If a unit appears with some power, the conversion factor must appear with the same power.

Links:

• Unit Converter
• Reference (SI units)

Accuracy, Precision, Uncertainty

The precision of a measurement refers to how close the agreement is between repeated measurements (which are repeated under the same conditions).

All measurements contain some amount of uncertainty. The uncertainty in a measurement, A, is often denoted as δA ("delta A"), so the measurement result would be recorded as A ± δA.
Percent uncertainty % uncertainty = (δA /A)*100%.

Estimates

To understand the essence of a physical situations order of magnitude estimates, which round off values to the nearest power of ten, are often all that is needed.  Before doing an exact numerical calculation, always try to make order of magnitude estimates.  Check the consistency of the units for your approach to a problem!

Module1: Question 1

(a)  Look at a person and a meter stick.  Estimate (order of magnitude) the volume of a human body, in m³.

(b)  Estimate the approximate number of atoms in a bacterium. Assume that the average mass of an atom in the bacterium is 10⁻²⁷ kg and the mass of a bacterium is on the order of 10⁻¹⁵ kg. Then estimate the number of cells in an adult human assuming the mass of an average cell is ten times the mass of a bacterium.

Discuss this with your fellow students in the discussion forum!