The key word is CHANGE!
Consider a function y(x) of the variable x. A plot of an arbitrary function y(x) versus x is shown below. We can find the change in y, ∆y, given a change in x, ∆x. ∆y/∆x defines the slope of a straight line connecting the points A and B in the figure below. As B moves closer to A, this straight line approaches the line tangent to y(x) at point A.
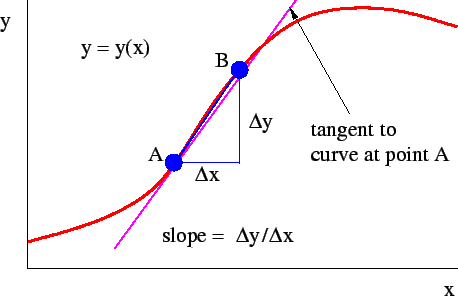
The slope of this tangent line is the derivative of y with respect to x and is denoted dy/dx. Since a tangent line to the function y(x) can be defined at any point x, the derivative itself is a function of x. We can denote it by g(x).
g(x) = dy/dx
The slope of the tangent line at some point on the function y(x) may be approximated by the slope of a line connecting two points, A and B, set a finite distance apart on the curve.
dy/dx ~ ∆y/∆x
The smaller we make the distance ∆x, the better the approximation becomes. In the limit ∆x --> 0, i.e. when the distance between A and B becomes infinitesimally small, the approximation becomes exact.Link: Exploring derivatives using a spreadsheet
Since the tangent line to the function y(x) can be defined at any point x, the derivative itself is a function of x. The table below lists derivatives of some common functions. In all expressions a and b are constants.
| y(x) = | dy/dx = |
|---|---|
| a*xb | a*b*xb-1 |
| a*exp(bx) | a*b*exp(bx) |
| a*sin(bx) | a*b*cos(bx) |
| a*cos(bx) | -a*b*sin(bx) |
| a*ln(x) | a/x |
Often we will encounter functions of the form y(x) = a*exp(bx + c), y(x) = a*sin(bx + c), and y(x) = a*cos(bx + c).
The derivatives of those functions are given below.
| y(x) = | dy/dx = |
|---|---|
| a*exp(bx + c) | a*b*exp(bx + c) |
| a*sin(bx + c) | a*b*cos(bx + c) |
| a*cos(bx + c) | -a*b*sin(bx + c) |