Many of the objects we encounter in everyday life are in motion or have parts that are in motion.  Motion is the rule, not the exception.  The physical laws that govern the motion of these objects are universal, i.e. all the objects move according to the same rules, and one of the goals of this class is to understand these rules.

When an object moves, its position changes as a function of time. 

The position of an object is given relative to some agreed upon reference point.  It is not enough to just specify the distance from the reference point.  We also have to specify the direction.  Distance is a scalar quantity, it is a number given in some units.  Position is a vector quantity.  It has a magnitude as well as a direction.  The magnitude of a vector quantity is a number (with units) telling you how much of the quantity there is and the direction tells you which way it is pointing.  A unit vector is a direction indicator.  It is a dimensionless vector with magnitude 1, used to specify a direction.  In text, vector quantities are usually printed in boldface type or with an arrow above the symbol.  Thus, while d = distance, d = displacement.

Links:
Scalars and Vectors  (Please explore!)
Vector Direction

Position

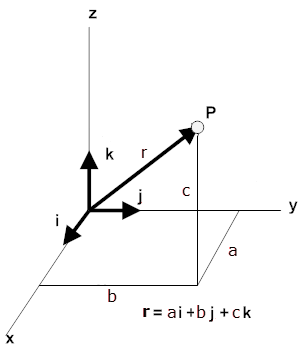A convenient way to specify the position of an object is with the help of a coordinate system.  We choose a fixed point, called the origin and three directed lines, which pass through the origin and are perpendicular to each other.  These lines are called the coordinate axes of a three-dimensional rectangular (Cartesian) coordinate system and are labeled the x-, y-, and z-axis.  Three numbers with units specify the position of a point P.  These numbers are the x-, y-, and z-coordinates of the point P.  The coordinates of the point P in the diagram to the right are (a, b, c). 

The coordinates of the point P are the components of the position vector.  A unit vector pointing in the x-direction has a x-component of 1 and y- and z- components of zero.  It is denoted by i.  Similarly, a unit vector pointing in the y-direction is denoted by j, and a unit vector pointing in the z-direction is denoted by k.  Unit vectors are direction indicators.

The components of any vector add up to form the vector itself.
The position vector of a point P with coordinates (a, b, c)  may be written in terms of its components as
r = ai + bj + ck.  
The magnitude of the position vector is its length r.  It depends on the choice of the origin of the coordinate system.  It is the straight-line distance of P from the origin.

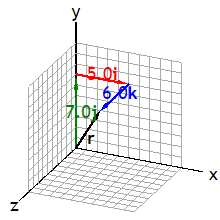
Below is a 3D representation of a position vector r = ai + bj +ck.   Please click on the image!
(Use a modern browser.  The 3D apps do not work in Internet Explorer or older browsers.)
To get the best view, change the viewport by dragging the mouse and zoom in or out as needed.
Click the buttons to choose a different vector or a different scheme for adding the component vectors.

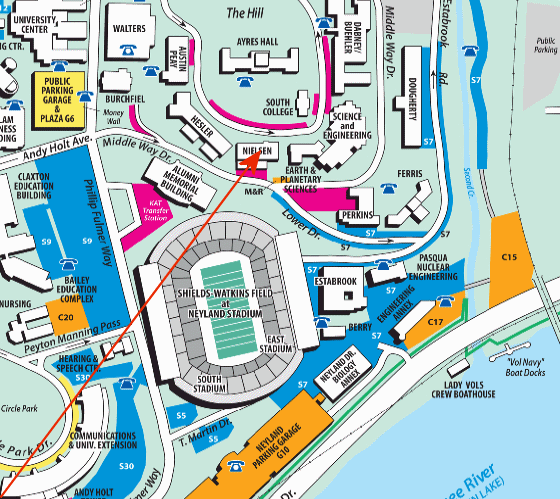
Example:

Position vector of the Nielsen Physics Building on a small map with the lower left corner as the origin.

Displacement

A change in position is called a displacement.  The diagram below shows the positions P₁ and P₂ of a player at two different times. 

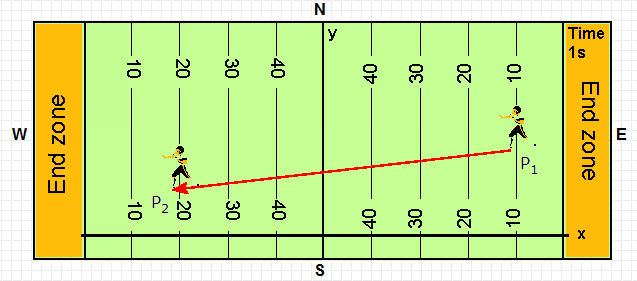
The arrow pointing from P₁ to P₂ is the displacement vector. 
Its magnitude is the straight-line distance between P₁ and P₂. 
The components of the displacement vector from P₁ to P₂ are (x₂ - x₁) along the x-axis, (y₂ - y₁) along the y-axis. 
The displacement vector d  from P₁ to P₂ may be written as d = (x₂ - x₁)i + (y₂ - y₁)j.
The displacement d is (x₂ - x₁) units in the x-direction plus (y₂ - y₁) units in the y-direction.
The magnitude of the displacement is d = ((x₂ - x₁)² + (y₂ - y₁)²)^½.  This follows from the Pythagorean theorem.

The distance between two points P₁ with coordinates (x₁, y₁, z₁) and P₂ with coordinates (x₂, y₂, z₂) is
d = ((x₂ - x₁)² + (y₂ - y₁)²  + (z₂ - z1)^2)½.

• The distance d is the magnitude of the displacement vector d.
• The direction of the displacement vector d is the directed line segment from the P₁ to P₂.
• We call this directed line segment a geometrical or graphical representation of the vector d.
• We draw an arrow head at P₂ to indicate that the line segment starts at the P₁ and ends at P₂.

The triple of real numbers d_x = (x₂ - x₁), d_y = (y₂ - y₁), d_z = (z₂ - z₁) are called the Cartesian components of d.

Link:  Distance and Displacement  (Please explore!)

Problem:

A football quarterback runs 15.0 m straight down the playing field (in the positive x direction) in 2.50 s.  He is then hit and pushed 3.00 m straight backward in 1.75 s.  He breaks the tackle and runs straight forward another 21.0 m in 5.20 s.  Calculate his displacement vector and the total distance traveled.

Solution:

• Reasoning:
  Choose a coordinate system so you can track the player.
• Details of the calculation:
  Choose your coordinate system so the player starts at x = 0.  After 2.5 s, he ends up at x = 15 m.
  He then moves backward 3 m, and ends up at x = 12 m after another 1.75 s.
  He moves forward 21 m in the next 5.2 s and ends up at x = 12 m + 21 m = 33 m.
  His displacement vector is d = (33 m)i, i.e. 33 m forward.
  His total distance traveled is 15 m + 3 m + 21 m = 39 m.
  
  Note:  The total distance traveled is NOT the straight-line distance from the start to the end point if an object does not move in a straight line without changing direction.

Problem:

While traveling along a straight interstate highway you notice that the mile marker reads 260.  You travel until you reach the 150-mile marker, and then retrace your path to the 175-mile marker.  What is the magnitude of your resultant displacement from the 260-mile marker?

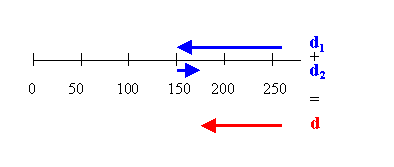
Solution:

• Reasoning:
  The resultant displacement is the vector d, the sum of two vectors d₁ and d₂ which point in opposite directions.
• Details of the calculation:
  The sum of the two displacement vectors is d = d₁ + d₁ = (-110 m) + 25 m = -85 m.
  You can also argue in the following way.
  For the total displacement it only matters where you start and where you stop.
  d = position 2 - position 1 = 175 m - 260 m = -85 m.

Problem:

The tip of a  helicopter blade is 5.00 m from the center of rotation.  For one revolution of the blade, calculate the displacement vector and the total distance traveled for the tip of the blade.

Solution:

• Reasoning:
  After one revolution, the tip returns to is original position.  Its displacement vector d = 0.
• Details of the calculation:
  The total distance traveled by the tip equals the circumference of a circle of radius r = 5 m. 
  Circumference = 2πr = 31.42 m.
  The total distance traveled by the tip is 31.42 m.

The displacement vector has the same magnitude and direction, independent of the choice of origin of the coordinate system.  The magnitude and direction of the displacement vector, however, depend on the reference frame in which the coordinate system is anchored and at rest.

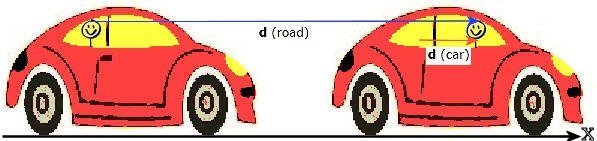
Example:

A car has moved forward a distance of 6 m, while a child has moved forward from the back seat to the front seat a distance of 1 m.

• Using the car as a reference frame and anchoring the coordinate system in the car, the displacement of the child is d(car) = (1 m)i.
• Using the road as a reference frame and anchoring the coordinate system on the road, the displacement of the child is d(road) = (6 m)i + (1 m)i = (7 m)i.