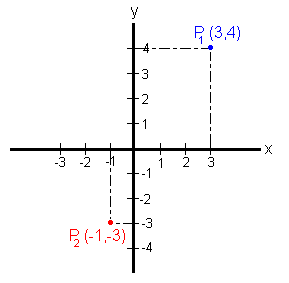 To uniquely specify vector quantities we need a
reference point and reference lines, i.e. we need a
coordinate system.
To uniquely specify vector quantities we need a
reference point and reference lines, i.e. we need a
coordinate system.In physics, quantitative models are developed on the basis of measurements. They need to be tested by making more measurements. Measurements are made in standard increments, called units. Without units a measurement is meaningless.
Some quantities are specified completely by a magnitude, which is to say by a
number and the appropriate units.
A real number by itself is called a
scalar, and such quantities are called scalar quantities. Symbols that denote these scalar quantities are
normal letters.
temperature (T) T = 10 oC
time interval (t) t = 5 s
mass (m) m = 3 kg
Other quantities are specified by a magnitude and a direction. By
direction, we mean a direction in space.
Such quantities are called
vector quantities. Symbols that denote
these vector quantities are bold letters, or normal letters with arrows drawn
above.
displacement (d) d = 10 m north
velocity (v)
v = 3 m/s eastward
force (F)
F = 9 N up
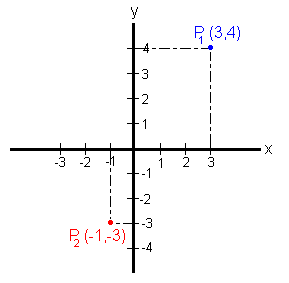 To uniquely specify vector quantities we need a
reference point and reference lines, i.e. we need a
coordinate system.
To uniquely specify vector quantities we need a
reference point and reference lines, i.e. we need a
coordinate system.
The Cartesian coordinate
system is the most commonly used coordinate system. In
two dimensions, this system consists of a pair of lines on a flat
surface or plane, that intersect at right angles. The lines are
called axes and the point at which
they intersect is called the origin.
The axes are usually drawn horizontally and vertically and are referred
to as the x- and y-axis, respectively.
A point in the plane with
coordinates (a, b) is a units to the right of the y axis and b units up
from the x axis if a and b are positive numbers.
If a and b are
both negative numbers, the point is a units to the left of the y axis
and b units down from the x axis.
In the figure on the right point
P1 has coordinates (3, 4), and point P2 has
coordinates (-1, -3).
In three-dimensional Cartesian coordinates, the z-axis is added so that
there are three axes all perpendicular to each other.
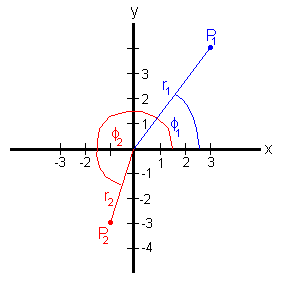 In the polar coordinate system,
each point in the plane is assigned coordinates (r, φ) with respect to a
fixed line in the plane called the axis
and a point on that line called the pole.
For a point in the plane, the r-coordinate is the distance from the
point to the pole, and the φ-coordinate is the counterclockwise angle
between the axis and a line joining the origin to the point.
In the polar coordinate system,
each point in the plane is assigned coordinates (r, φ) with respect to a
fixed line in the plane called the axis
and a point on that line called the pole.
For a point in the plane, the r-coordinate is the distance from the
point to the pole, and the φ-coordinate is the counterclockwise angle
between the axis and a line joining the origin to the point.
The
r-coordinate is always positive and the range of φ is from 0 to 2π (360o).
To be able to transform from Cartesian to polar coordinates and vice
versa, we let the axis of the polar coordinate system coincide with the
x-axis of the Cartesian coordinate system and the pole coincide with the
origin.
In the figure on the right the Point P1 has
polar coordinates (r1, φ1) = (5, 53.1o),
and the point P2 has polar coordinates (r2, φ2)
= (3.16, 251.6o ).
The transformation equations are
x = r cosφ, y = r sinφ.
r = (x2 + y2)½, φ =
tan-1(y/x).
Cylindrical coordinates and spherical coordinates are
two different extensions of polar coordinates to three dimensions.
Once we have picked a coordinate system, a physical
vector quantity in two dimensions can be represented by a pair of
numbers.
If we pick Cartesian coordinates, there numbers are the vector's projections on the axes of
the Cartesian coordinate
system.
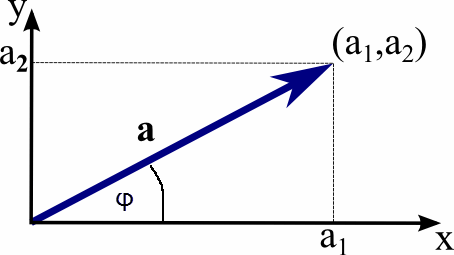 The vector
a in the figure on the right has x-component
a1 and y-component a2.
The vector
a in the figure on the right has x-component
a1 and y-component a2.
Its length or magnitude is a = (a12 + a22)½.
This follows from the
Pythagorean theorem.
The polar angle of a, i.e. the angle a makes with the
x-axis is φ.
A vector A lies in the xy-plane.
(a) For what orientations of
A will both of its rectangular components be negative?
(b) For what
orientation will its components have opposite signs?
Solution:
Note: The magnitude of a vector tells you how long it is. It is a number
(with units). If the vector is a velocity vector, then its magnitude has units of speed
(m/s), if it is a displacement vector, then its magnitude has units of distance
(m), etc.
The direction in two dimensions, i.e. in a plane, is the angle the vector makes
with the x-axis, measured counterclockwise from the x-direction.
You need a coordinate system (reference frame) before you specify the direction.
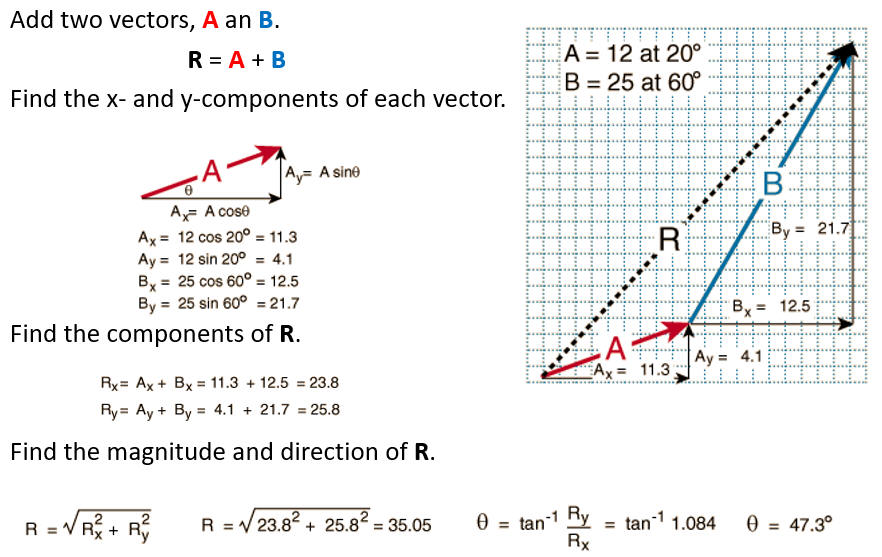
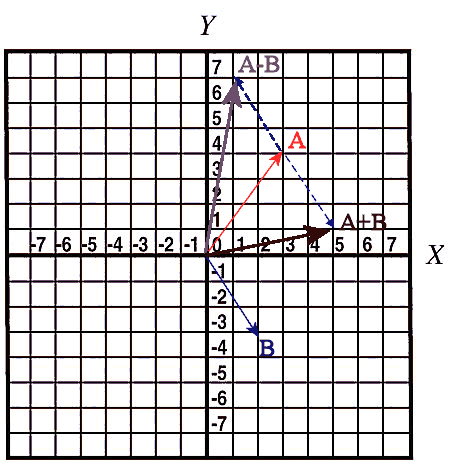 Adding vectors
Adding vectorsTo add physical vectors, they have to have the same units. To find the sum of two physical vector quantities with the same units algebraically, we add the x, y, and z-components of the individual vectors.
Let vector v1 have components (3, 4) and vector
v2 have components (2, -3).
Let v =
v1 + v2 be the sum of the two vectors.
Then the components of
v are (3+2, 4+(-3) = (5, 1).
The magnitude of the vector v is v = (25 + 1)½ = 5.1,
and the angle v makes with the x-axis is φ = tan-1(1/5)
= 0.197 rad = 11.3o.
 To subtract vector
v2 from vector v1
we subtract the components of vector v2 from the
components of vector v1.
To subtract vector
v2 from vector v1
we subtract the components of vector v2 from the
components of vector v1.
Let vector v1 have components (3, 4) and vector
v2 have components (2, -3).
Let v =
v1 - v2 be the difference of the two
vectors.
Then the components of v are (3-2, 4-(-3) = (1,
7).
The magnitude of the vector v is v = (1 + 49)½ = 7.1
and the angle v makes with the x-axis is φ = tan-1(7/1)
= 1.429 rad = 81.9o.
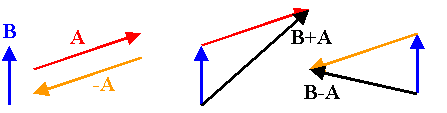
The graphical representation of a vector quantity is a directed line
segment. To find the sum of two physical vector quantities with
the same units graphically we line up the arrows, tail to tip.
The sum is the arrow drawn from the tail of the first vector to the tip
of the last vector. To subtract a vector v2 from
a vector v1 we we invert vector v2
and add it to vector v1.
Let A be an arbitrary vector. The vector -A has the
same length, and points in exactly the opposite direction.
Subtracting the vector A from another vector means adding the
vector -A to the other vector.
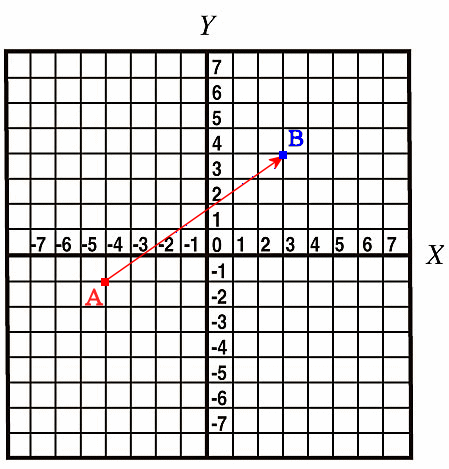 Example:
Example:The displacement vector
Let d represent the displacement vector from point
A with coordinates (x1, y1) = (-4, -1) to point B
with coordinates (x2, y2) = (3, 4).
The displacement vector is the difference between the position vectors
A and B, d = B - A.
Its components
are
dx = (x2 - x1) = 3 - (-4) = 7, dy
= (y2 - y1) = 4 - (-1) = 5.
The displacement vector d has magnitude d = (49 + 25)½
= 8.6.
The angle d makes with the x-axis is φ = tan-1(5/7) =
0.62 rad = 35.5o.
Link: Lesson 1: Vectors - Fundamentals and Operations
Please study this material from "the Physics Classroom".