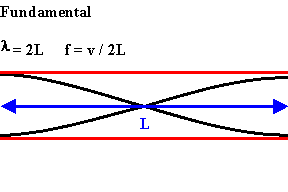
 The
longest standing wave in a tube of length L with two open ends
has displacement antinodes (pressure nodes) at both ends.
The
longest standing wave in a tube of length L with two open ends
has displacement antinodes (pressure nodes) at both ends.It is called the fundamental or first harmonic.
When a sound wave hits a wall, it is partially absorbed and partially reflected. A person far enough from the wall will hear the sound twice. This is an echo. In a small room the sound is also heard more than once, but the time differences are so small that the sound just seems to loom. This is known as reverberation.
Music is the sound that is produced by instruments or voices. To play most musical instruments you have to create standing waves on a string or in a tube or pipe. The perceived pitch of the sound is related to the frequency of the wave. The higher the frequency, the higher is the pitch.
Wind instruments produce sounds by means of vibrating air columns. To play a wind instrument you push the air in a tube with your mouth or a reed. The air in the tube starts to vibrate with the same frequency as your lips or the reed. Resonance increases the amplitude of the vibrations, which can form standing waves in the tube. The length of the air column determines the resonant frequencies. The mouth or the reed produces a mixture if different frequencies, but the resonating air column amplifies only the natural frequencies. The shorter the tube the higher is the pitch. Many instruments have holes, whose opening and closing controls the effective pitch.
We can create a standing wave in a tube, which is open on both ends, and in a tube, which is open on one end and closed on the other end. Open and closed ends reflect waves differently. The closed end of a tube is an antinode in the pressure (or a node in the longitudinal displacement). The open end of a tube is approximately a node in the pressure (or an antinode in the longitudinal displacement).
 The
longest standing wave in a tube of length L with two open ends
has displacement antinodes (pressure nodes) at both ends.
The
longest standing wave in a tube of length L with two open ends
has displacement antinodes (pressure nodes) at both ends.
It is called the fundamental
or first harmonic.
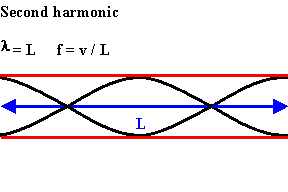 The next longest standing wave in a tube of length L
with two open ends is the second harmonic.
The next longest standing wave in a tube of length L
with two open ends is the second harmonic.
It also has
displacement antinodes at each end.
An integer number of half wavelength have to fit into the tube of length L.
L = nλ/2, λ = 2L/n, f = v/λ = nv/(2L).
For a tube with two open ends all frequencies fn = nv/(2L) = nf1, with n equal to an integer, are natural frequencies.
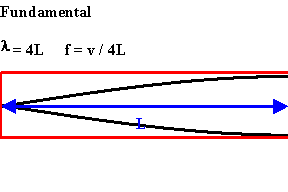 The longest standing wave in a tube of length L with one open end and one
closed end has a displacement antinode at the open end and a displacement node
at the closed end. This is the fundamental.
The longest standing wave in a tube of length L with one open end and one
closed end has a displacement antinode at the open end and a displacement node
at the closed end. This is the fundamental.
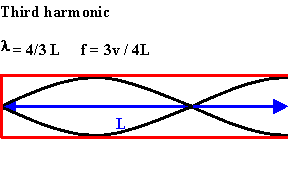 The next longest standing wave in a tube of length L
with one open end and one closed end is the third harmonic.
The next longest standing wave in a tube of length L
with one open end and one closed end is the third harmonic.
An odd-integer number of quarter wavelength have to fit into the tube of length L.
L = nλ/4, λ = 4L/n, f = v/λ = nv/(4L), n = odd.
For a tube with one open end and one closed end all frequencies fn = nv/(4L) = nf1, with n equal to an odd integer are natural frequencies, i.e. only odd harmonics of the fundamental are natural frequencies.
Link: The Physics Classroom: Sound Waves and Music (Lessons 4 and 5)
What length should a pipe open at both ends have to produce a fundamental frequency of 110 Hz on a day when the speed of sound is 343 m/s?
Solution:
Is the wavelength of the fundamental standing wave in a tube open at both
ends greater than, equal to, or less than the wavelength of the fundamental
standing wave in a tube of the same length with one open end and one closed end?
Solution:
Why does a clarinet play a lower note than a flute when both
instruments are about the same length?
Solution:


External links:
Visualizing standing sound waves (Youtube)
How Do Woodwind
Instruments Work? (unsw.edu.au)
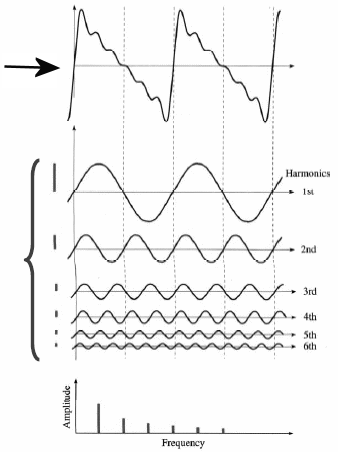 The quality of a sound depends on the relative
intensities of the waves with the natural frequencies. It depends
on the spectrum of the sound.
The sound quality of a musical instrument is called its
timbre. A sinusoidal sound wave of
frequency f is a pure tone. A note played by a musical instrument
is not a pure tone. Its wave function is not sinusoidal, i.e. it
is not of the form ∆P(x,t) = ∆Pmaxsin(kx
- ωt + φ). The wave function is a sum
of sinusoidal wave functions with frequencies nf, (n = 1, 2, 3, ...,)
with different amplitudes, which decrease as n increases. The
harmonic waves with different frequencies which sum to the final wave
are called a Fourier series.
Breaking up the original sound wave into its sinusoidal components is
called Fourier analysis.
The quality of a sound depends on the relative
intensities of the waves with the natural frequencies. It depends
on the spectrum of the sound.
The sound quality of a musical instrument is called its
timbre. A sinusoidal sound wave of
frequency f is a pure tone. A note played by a musical instrument
is not a pure tone. Its wave function is not sinusoidal, i.e. it
is not of the form ∆P(x,t) = ∆Pmaxsin(kx
- ωt + φ). The wave function is a sum
of sinusoidal wave functions with frequencies nf, (n = 1, 2, 3, ...,)
with different amplitudes, which decrease as n increases. The
harmonic waves with different frequencies which sum to the final wave
are called a Fourier series.
Breaking up the original sound wave into its sinusoidal components is
called Fourier analysis.
Fourier analysis implies that any wave pattern can be produced by superimposing the appropriate sinusoidal waves. Fast computer algorithms exist that calculate the required amplitudes. Fourier synthesis the basis for electronic music.