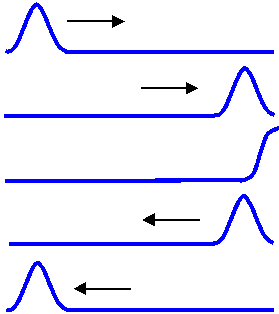
This wave pulse is totally reflected from a rope with a loose end. It is not inverted upon reflection.
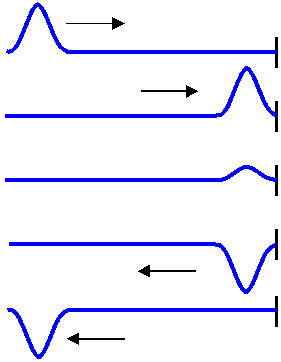
This wave pulse is totally reflected from a rope with a fixed end. Upon reflection, it is inverted.
Two or more waves traveling in the same medium travel independently and can pass through each other. In regions where they overlap, the disturbances add like vectors.
Consider two waves with the same amplitude, frequency, and wavelength that are travelling in opposite directions on a string. Using the trigonometric identities sin(a + b) = sin(a)cos(b) + cos(a)sin(b) we write the resulting displacement of the string as a function of time as
y(x,t) = A sin(kx - ωt) + A sin(kx + ωt) = 2A sin(kx)cos(ωt).
This wave is no longer a traveling wave because the position and time dependence have been separated. All sections of the string oscillate either in phase or 180o out of phase. The section of the string at position x oscillates with amplitude 2A sin(kx). No energy travels along the string. There are sections that oscillate with maximum amplitude and there are sections that do not oscillate at all. We have a standing wave.
Please watch: YouTube: Standing wave
W
When a wave in a medium reaches the end of the medium, it often is reflected and travels back in the opposite direction. Similarly, when the medium through which a wave travels abruptly changes, the wave may be partially or totally reflected. When a wave pulse traveling along a rope reaches the end of the rope, it is totally reflected. The details of the reflection depend on if the end of the rope is tied down and fixed, or if it is allowed to swing loose.

This wave pulse is totally reflected from a rope with a loose end. It is not inverted upon reflection.

This wave pulse is totally reflected from a rope with a fixed end. Upon reflection, it is inverted.
When two wave pulses traveling along the same rope in opposite direction meet, they interfere.
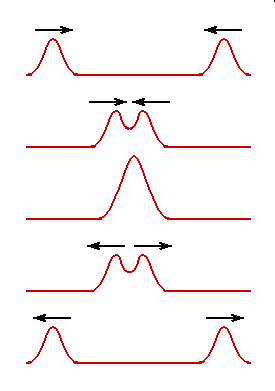
The two wave pulses above interfere constructively when they meet.
These two wave pulses interfere destructively.
External link: Reflection of a transverse wave from a boundary (Please explore!)
When a periodic wave is totally reflected, then the incident wave and the reflected wave travel in the same medium in opposite directions and interfere. When the medium is of finite extend, then the waves reflect on both ends. Consider a string fixed on both ends. In general the waves reflected from both ends produce an interference pattern that is complex and confusing. But when the wavelength of the waves is just right, so that an integral number of half wavelengths fit into the length of the string, a standing wave forms.
All standing waves are characterized by positions along the medium which are standing still. Such positions are referred to as nodes. Nodes are the result of the meeting of a crest with a trough. This leads to a point of no displacement. Standing waves are also characterized by antinodes. These are positions along the medium where the particles oscillate about their equilibrium position with maximum amplitude. Antinodes are the result of a crest meeting a crest and a trough meeting a trough. Standing wave patterns are always characterized by an alternating pattern of nodes and antinodes.
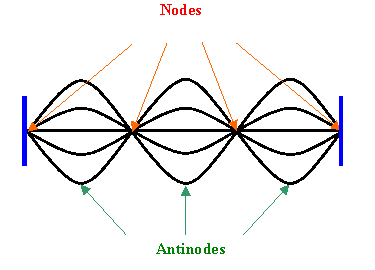
Standing waves of many different wavelengths can be produced on a string with two fixed ends, as long as an integral number of half wavelength fits into the length of the string. Each wavelength corresponds to a particular frequency and is known as a harmonic. Wavelength and frequency are related through λf = v, where v is the speed of waves along the string. For a given v, the shorter the wavelength, the higher is the frequency. The lowest possible frequency of a standing wave is known as the fundamental frequency or the first harmonic. Only half a wavelength fits into the length of the string.

First harmonic
Link: Standing waves on a string; first harmonic
The second lowest frequency at which a string could vibrate is known as the second harmonic, the third lowest frequency is known as the third harmonic, and so on.
Links:

Second harmonic

Third harmonic
The frequency associated with each harmonic depends on the speed with which waves move through the medium and the wavelength of the wave. For a string, the speed of the waves is a function of the mass per unit length μ = m/L of the string and the tension F in the string.
v = √(F/μ).
The speed of waves on a string does not depend on the wavelength or frequency.
A rope has a mass of 2 kg and a length of 10 m. It is stretched with a tension of 50 N and fixed at both ends. What is the frequency of the first harmonic on this rope?
Solution:
If a guitar string is simply plucked, the fundamental frequency dominates. The first harmonic can be produced by touching the string lightly in the middle when plucking it. Touching the string lightly one-third the length of the string from one end will produce the second harmonic.
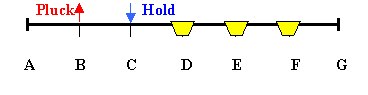
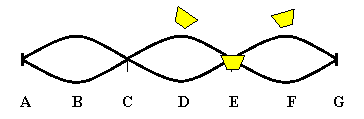
A guitar string is stretched from point A to G. Equal intervals are marked off. Paper riders are placed on the string at D, E, an F. When the string is pinched at C and twanged at B, which riders jump off?
Solution:
Standing wave patterns can be set up in almost any structure. In two and three dimensions, the patterns can become quite complex. When a structure is vibrating with its fundamental frequency, then all the particles oscillate in phase with the same frequency. A harmonic driving force with the same frequency can very efficiently pump energy into this mode. At resonance, the amplitude of the standing wave can increase without limit, until the structure is damaged. (Since we do not have a traveling wave, energy pumped into the structure can only be dissipated through damping.)
A famous example of a structure driven into resonance in a windstorm and collapsing is the Tacoma Narrows bridge failure. The original, 5,939-foot-long Tacoma Narrows Bridge, was opened to traffic on July 1, 1940 after two years of construction, linking Tacoma and Gig Harbor. It collapsed 4 months and 7 days after it opened. The collapse occurred during a 42-mile-per-hour wind storm on November 7, 1940, around 11:00 am.
Link: Tacoma Narrows Bridge Failure (Youtube)