A wave pulse is a disturbance that moves through a medium.A wave pulse is a disturbance that moves through a medium.
A periodic wave is a periodic disturbance that moves through a medium. The medium itself goes nowhere. The individual atoms and molecules in the medium oscillate about their equilibrium position, but their average position does not change. As they interact with their neighbors, they transfer some of their energy to them. The neighboring atoms in turn transfer this energy to their neighbors down the line. In this way the energy is transported throughout the medium, without the transport of any matter.
The animation on the right portrays a medium as a
series of particles connected by springs. As one individual particle is
disturbed, and then returns to its initial position, it transmits the disturbance to the next interconnected
particle. This disturbance continues to be passed on to the next
particle. The result is that energy is transported from one end of the
medium to the other end of the medium without the actual transport of
matter. Each particle returns to its original position.
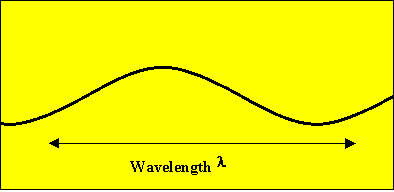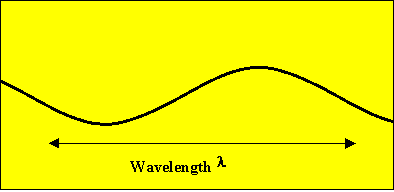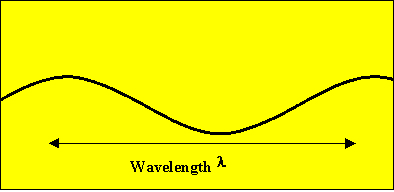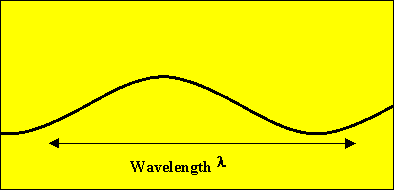Periodic waves are characterized by a
frequency, a wavelength, and by their speed.
The wave frequency f is the oscillation frequency of the individual
atoms or molecules. The period T = 1/f is the time it takes any
particular atom or molecule to go through one complete cycle of its
motion. The wavelength λ is the distance along the direction of
propagation between two atoms which oscillate in phase.
In a periodic wave, a pulse travels a distance of one wavelength λ in a time equal to one period T. The speed v of the wave can be expressed in terms of these quantities.
v = λ/T = λf
The relationship v = λf holds true for any periodic wave.
If the individual atoms and molecules in the medium move with simple harmonic motion, the resulting periodic wave has a sinusoidal form. We call it a harmonic wave or a sinusoidal wave.
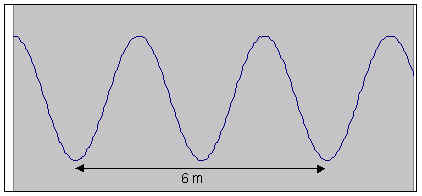Problem:A wave on a rope is shown on the right at some time t. What is the wavelength of this wave? If the frequency is 4 Hz, what is the wave speed?
Solution:
Suppose that a water wave coming into a dock has a speed of 1.5 m/s and a wavelength of 2 m. With what frequency does the wave hit the dock?
Solution:
Solution:
If the displacement of the individual atoms or
molecules is perpendicular to the direction the wave is traveling, the
wave is called a transverse wave.
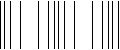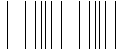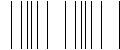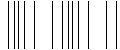If the displacement is parallel to the direction of
travel the wave is called a longitudinal wave
or a compression wave.
Transverse waves can occur only in solids, whereas longitudinal waves can travel in solids, liquids, and gases. Transverse motion requires that each particle drag with it adjacent particles to which it is tightly bound. In a fluid this is impossible, because adjacent particles can easily slide past each other. Longitudinal motion only requires that each particle push on its neighbors, which can easily happen in a liquid or gas. The fact that longitudinal waves originating in an earthquake pass through the center of the earth while transverse waves do not is one of the reasons the earth is believed to have a liquid outer core.
Link: Transverse and Longitudinal Wave motion
Consider a transverse harmonic wave traveling in the positive x-direction. Harmonic waves are sinusoidal waves. The displacement y of a particle in the medium is given as a function of x and t by
y(x,t) = A sin(kx - ωt + φ)
Here k is the wave number, k = 2π/λ, and ω = 2π/T = 2πf is the angular frequency of the wave. φ is called the phase constant.
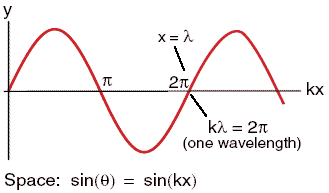At a fixed time t the displacement y varies as a function of
position x as A sin(kx) = A sin[(2π/λ)x]
The phase constant φ is determined by the initial conditions of the
motion. If at t = 0 and x = 0 the displacement y is zero, then φ =
0 or π. If at t = 0 and x = 0 the displacement has its maximum
value, then φ = π/2. The quantity kx - ωt + φ is
called the phase.
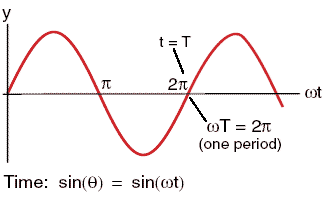At a fixed position x the displacement y varies as a function of
time as A sin(ωt) = A sin[(2π/T)t] with a convenient
choice of origin.
For the transverse harmonic wave y(x,t) = Asin(kx - ωt + φ) we may also write
y(x,t) = A sin[(2π/λ)x - (2πf)t + φ] = A sin[(2π/λ)(x - λft) + φ],
or, using λf = v and 2π/λ = k,
y(x,t) = A sin[k(x - vt) + φ].
This wave travels into the positive x direction. Let φ = 0. Try to follow some point on the wave, for example a crest. For a crest we always have k(x - vt) = π/2. If the time t increases, the position x has to increase, to keep k(x - vt) = π/2.
For a transverse harmonic wave traveling in the negative x-direction we have
y(x,t) = A sin(kx + ωt + φ)= A sin(k(x + vt) + φ).
For a crest we always have k(x + vt) = π/2. If the time t increases, the position x has to decrease, to keep k(x + vt) = π/2.
A traveling wave is described by the equation y(x,t) = (0.003) cos(20 x + 200 t ), where y and x are measured in meters and t in seconds. What are the amplitude, frequency, wavelength, speed and direction of travel for this wave?
Solution:
To visualize the traveling wave, download this Excel spreadsheet. Macros must be enabled.
The amplitude A of a wave is the maximum displacement of the individual particles from their equilibrium position. The energy density E/V (energy per unit volume) contained in a wave is proportional to the square of its amplitude.
E/V is proportional to A2
The power P or energy per unit time delivered by the wave if it is absorbed is proportional to the square of its amplitude times its speed.
P is proportional to A2v.
To increase power of a wave by a factor of 50, by what factor should the amplitude be increased? (Assume the speed v does not depend on the amplitude.)
Solution:
Link: The Physics Classroom: Waves
Two or more waves traveling in the same medium travel independently and can pass through each other. In regions where they overlap we only observe a single disturbance. We observe interference. When two or more waves interfere, the resulting displacement is equal to the vector sum of the individual displacements. If two waves with equal amplitudes overlap in phase, i.e. if crest meets crest and trough meets trough, then we observe a resultant wave with twice the amplitude. We have constructive interference. If the two overlapping waves, however, are completely out of phase, i.e. if crest meets trough, then the two waves cancel each other out completely. We have destructive interference.
Link: Superposition Principle of Wave