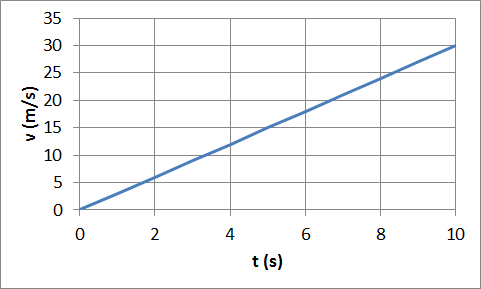
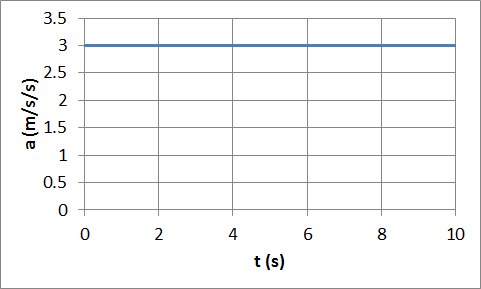
Let us assume at t = 0 a cart is leaving the origin with zero initial velocity and constant acceleration of 3 m/s² in the positive x-direction. 
Then a =  ∆v/∆t,  v_f - v_i = a(t_f - t_i), and since v_i = t_i = 0 we have v(t) = a*t = (3 m/s²)*t.
The velocity (m/s) versus time (s) graph is a straight line with i a slope of 3.
The acceleration (m/s²) versus time (s) graph yields a straight line (a = 3) with zero slope.

 

Kinematic equations for one-dimensional motion with constant acceleration

Let us consider one-dimensional motion in the x-direction.
Let us make this explicit by using the subscript x. 
The average acceleration equals the instantaneous acceleration.  From

a_x = (v_xf - v_xi)/(t_f - t_i)

we obtain

a_x(t_f - t_i) = (v_xf - v_xi),

or

v_xf = v_xi + a_x∆t.

The velocity versus time graph is a straight line. 
The average velocity in a time interval ∆t therefore is just the sum of the final and the initial velocities divided by 2,

v_x(avg) = (v_xf + v_xi)/2.

The displacement is ∆x = v_x(avg)∆t.  We can rewrite this expression to obtain x_f - x_i = ½(v_xf + v_xi)∆t, or

x_f - x_i = v_xi∆t + ½a_x∆t².

We can also express the velocity as a function of the displacement.
∆x = ½(v_xf + v_xi)∆t = ½ (v_xf + v_xi)(v_xf - v_xi)/a_x = (v_xf² - v_xi²)/(2a_x) yields

v_xf² = v_xi² + 2a_x(x_f - x_i).

The equations in red are the kinematic equations for motion in the x-direction with constant acceleration.

What does a position versus time graph look like for motion in one dimension with constant acceleration?

Choose your coordinates so that x_i = t_i = 0.  Then x = v_it + ½at². 
This is the equation of a parabola.  The position versus time graph is a section of a parabola. 
In the limit a = 0 it becomes a straight line.

Examples:

Problem:

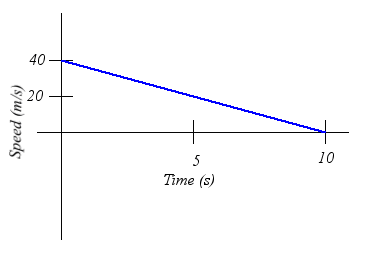The speed versus time graph on the right represents the motion of a car.  Approximately how far did the car travel during the first 5 seconds?

Solution:

• Reasoning:
  The speed versus time graph is a straight line.  We have motion with constant acceleration.  The slope of the graph represents the acceleration.
• Details of the calculation:
  The slope of the graph represents the acceleration.
  a_x = (v_xf - v_xi)/(t_f - t_i) = (-40 m/s)/(10 s ) = -4 m/s².
  For motion with constant acceleration we have
  ∆x_i = v_xi∆t + ½a_x∆t².
  After 5 s we have
  ∆x = 40m/s * 5 s - ½(4 m/s²)*(5 s)² = 150 m.
  During the first 5 seconds the car traveled 150 m.

Problem:

A particle is moving with velocity v₀ = 60 i (m/s) at t = 0.  Between t = 0 and t = 15 s the velocity decreases uniformly to zero.  What was the acceleration during this 15 s time interval?  What is the significance of the sign in your answer?

Solution:

• Reasoning:
  Since the velocity decreases uniformly, the acceleration is constant.  We therefore have a_x = (v_xf - v_xi)/∆t.
• Details of the calculation:
  a_x = (v_xf - v_xi)/∆t = (0 - 60 m/s)/15 s = -4m/s².
  The minus sign tells us that the acceleration vector is pointing in the negative x-direction.  The velocity and the acceleration vector point in opposite directions.  The particle is slowing down.

Problem:

Blood is accelerated from rest to v = 30.0 cm/s in a distance of 1.80 cm by the left ventricle of the heart.  Assume constant acceleration. 
(a)  Find the acceleration a.
(b)  For how long does the blood accelerate?
(c)  Is the answer reasonable when compared with the time for a heartbeat?

Solution:

• Reasoning:
  We assume motion with constant acceleration in one dimension.  The kinematic equations for this type of motion are
  v_xf = v_xi + a_x∆t,  x_f - x_i = v_xi∆t + ½a_x∆t²,  and v_xf² = v_xi² + 2a_x(x_f - x_i).
• Details of the calculation:
  (a)  Given:  v_i = 0, v_f = 0.3 m/s, ∆v = 0.3 m/s.
  x_i = 0, x_f = 0.018m, ∆x = 0.018 m.
  Kinematic equation:  v_xf² = v_xi² + 2a_x(x_f - x_i)
  Solve for a_x = (v_xf² -  v_xi²)/(2(x_f - x_i)) = (0.3 m/s)²/(0.036 m) = 2.5 m/s².
  
  (b)  v = at, t = v/a = (0.3 m/s)/(2.5 m/s) = 0.12 s
  or v_x(avg) = (v_xf + v_xi)/2 = 0.15 m/s.  ∆x = v_x(avg)∆t, 
  ∆t = ∆x/v_x(avg) = 0.018 m/(0.15 m/s) = 0.12 s.
  (c)  The figure below shows a typical electrocardiogram waveform.  0.12 s seems a reasonable acceleration time.