Let us define
projectile motion as the motion of a
particle through a region of three-dimensional space where it is subject to
constant acceleration.
For example, an
object moving through the air near the surface of the earth is subject
to the constant gravitational acceleration g, directed downward.
If no other forces are acting on the object, i.e. if the object
does not have a propulsion system and we neglect air resistance, then
the motion of the object is projectile motion. (This is the reason
motion with constant acceleration is called projectile motion.)
Assume that we want to describe
the motion of such an object, starting at time t = 0. Let us orient our
coordinate system such that one of the axes, say the y-axis, points
upward. ax = az = 0, ay = -g. We can
rotate our coordinate system about the y-axis until the velocity vector
of the object at t = 0 lies in the x-y plane, and we can choose the
origin of our coordinate system to be at the position of the object at t
= 0.
With the appropriate orientation of coordinate axes we
can treat projectile motion as motion in two dimensions with
vx = v0x, x = x0 + v0xt, vy= v0y
+ ayt, y = y0 + v0yt
+ ½ayt2.
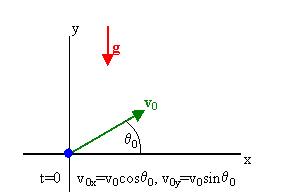The position vector
r and the velocity
vector v at time t have only components along the x- and y-axes. By
choosing a convenient orientation of our coordinate system we have simplified
the mathematics involved in solving a projectile motion problem.
If ay = -g, then
vx = v0x, x = x0 + v0xt, vy= v0y
- gt, y = y0 + v0yt - ½gt2.
Let ay = -g. If the initial velocity
v0 makes an angle θ0 with the x-axis, then
v0x = v0cosθ0 and v0y = v0sinθ0.
vx = v0cosθ0 =
constant, x = x0 + v0cosθ0t,
vy = v0sinθ0 - gt, y = y0 + v0sinθ0t - ½gt2.
We can solve x - x0 = v0cosθ0t for t in terms of x
- x0,
t = (x - x0)/(v0cosθ0)
and substitute this expression for
t into
y = y0 + v0sinθ0t - ½gt2.
We obtain
y = y0 + (x - x0)tan(θ0)
- g(x - x0)2/(2v02cos2(θ0)),
an equation for the path or trajectory
of the object. This equation is of the form y = y0+ a(x - x0) - b(x
- x0)2,
which is the equation of a parabola. If x0 = y0
= 0 the parabola passes
through the origin.
The trajectory for projectile motion is a section of a parabola.
Links:
Horizontally Launched Projectiles
Non-Horizontally Launched Projectiles
Example:
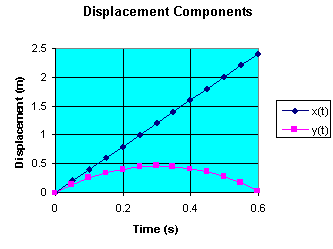Assume a projectile is launched with x0 = y0 = 0, v0x
= 4 m/s, v0y = 3 m/s.
We have
tanθ0 = v0y/v0x = 3/4, θ0 =
30.87o, v02 = v0x2
+ v0y2,
v0 = 5 m/s.
The projectile moves along a parabolic path until it
impacts the ground. Its coordinates as a function of time are
x = (4 m/s)t, y = (3 m/s)t - (4.9 m/s2)t2.
Its velocity components are vx
= 4 m/s, vy = (3 m/s) - (9.8 m/s2)t2.
| t |
x(t) |
y(t) |
vx(t) |
vy(t) |
| 0 |
0 |
0 |
4 |
3 |
| 0.05 |
0.2 |
0.13775 |
4 |
2.51 |
| 0.1 |
0.4 |
0.251 |
4 |
2.02 |
| 0.15 |
0.6 |
0.33975 |
4 |
1.53 |
| 0.2 |
0.8 |
0.404 |
4 |
1.04 |
| 0.25 |
1 |
0.44375 |
4 |
0.55 |
| 0.3 |
1.2 |
0.459 |
4 |
0.06 |
| 0.35 |
1.4 |
0.44975 |
4 |
-0.43 |
| 0.4 |
1.6 |
0.416 |
4 |
-0.92 |
| 0.45 |
1.8 |
0.35775 |
4 |
-1.41 |
| 0.5 |
2 |
0.275 |
4 |
-1.9 |
| 0.55 |
2.2 |
0.16775 |
4 |
-2.39 |
| 0.6 |
2.4 |
0.036 |
4 |
-2.88 |
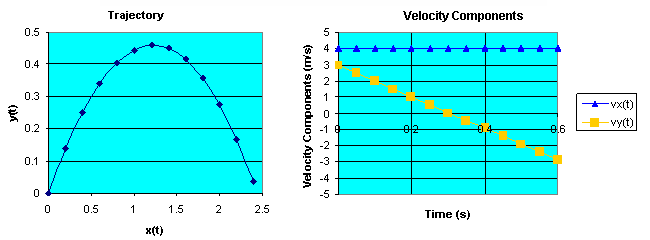
As we can see from the graphs
below, the projectile impacts
the ground after approximately 0.6 seconds. It reaches its maximum
height after approximately 0.3 seconds. Its range is approximately 2.4
meters. In approximately 0.3 seconds it has covered half its
range.
The trajectory for projectile motion is symmetric about the point of
maximum height. The projectile covers the
same horizontal distance reaching its maximum height as it does falling
from its maximum height back to the ground. It takes the projectile the
same amount of time reaching its maximum height as it does to fall from
the maximum height back to the ground. When the projectile reaches its
maximum height, after approximately 0.3 s, the
vertical component of its velocity is zero.
We can find the time when a projectile reaches its maximum height by setting vy
= vy0 - gt = 0 and solving for t. We find
tmax_height= vy0/g = v0sinθ0/g.
We can now find the range R by substituting t = 2tmax_height into the
equation for x(t).
R = v0cosθ02tmax_height
= (2v02cosθ0sinθ0)/g =
(v02sin2θ0)/g.
Similarly, we find the
maximum height h by substituting tmax_height into the
equation for y(t).
hmax = v0sinθ0tmax_height
- ½gt2max_height
= (v02sin2θ0)/2g.
Look at the expression for the range, R = (v02sin2θ0)/g. For a given v0,
R as a function of the launch angle θ0 has its maximum value
when sin2θ0 has its maximum value of 1. This happens when 2θ0
= 90o, or θ0 = 45o.
Rmax = v02/g is the maximum range
of a projectile launched with speed v0.
Link: Maximum Range
Problem:
One strategy in a snowball fight is to throw a snowball at a high angle over
level ground. While you opponent is watching the first one, you throw a second
snowball at a low angle timed to arrive before or at the same time as the first
one. Assume both snowballs are thrown with a speed of 25 m/s. The first is thrown at an angle of 70o with respect to
the horizontal.
(a) At what angle should the second snowball be thrown to arrive at the same
point as the first?
(b) How many seconds later should the second snowball be thrown after the first
to arrive at the same time?
Solution:
- Reasoning:
We have motion with constant acceleration in two dimensions, or projectile
motion.
The range of a projectile over level ground is R = (v02sin2θ0)/g.
The time in the air is 2tmax_height = 2vy0/g
= (2v0sinθ0)/g.
- Details of the calculation:
(a) R = (v02sin2θ0)/g.
If v0 is constant, the range is a function of θ0.
The
function sin2θ0 is symmetric about 2θ0 = 90o,
or θ0 = 45o.
It has the same value for θ0
= 45o + θ' as it has for θ0 = 45o
- θ'.
So a snowball thrown with θ0 = 70o
= 45o + 25o has the same range as a snowball
thrown with θ0 = 45o - 25o = 20o.
The second snowball should be thrown at an angle of 20o.
(b) The time a snowball is in the air is 2tmax_height = 2vy0/g
= (2v0sinθ0)/g.
The flight time of the first snowball
is 2tmax_height = 2v0sin70o/g = 4.79 s.
The flight time of the second snowball is 2tmax_height
= 2v0sin20o/g = 1.74 s.
The
second snowball must be thrown 3.05 s after the
first ball.
Problem:
An astronaut on a strange planet finds that she can jump a maximum
horizontal distance of 15 m if her initial speed is 3 m/s. What is the
free-fall acceleration on the planet?
Solution:
- Reasoning:
We have motion with constant acceleration in two dimensions, or projectile
motion.
The range of a projectile over level ground is R = (v02sin2θ0)/g.
To have maximum range for a given initial velocity, her launch angle must be
θ0
= 45o.
- Details of the calculation:
The astronaut's range is R = (v02sin2θ0)/g'
= v02sin90o/g' = v02/g'.
We have g' = v02/R = 0.6 m/s2.
Problem:
An owl is carrying a mouse to the chicks in its nest. Its
position at t = 0 is 4.0 m west (x0 = -4.0 m) and 12.0 m above the
center of the 30.0 cm diameter nest (y0 = 12.0 m). The owl is
flying east at 3.5 m/s at an angle 30o below the horizontal, i.e. vx0
= (3.5 m/s)cos(30o), vy0 = -(3.5 m/s)sin(30o), when it accidentally drops the mouse.
Is the owl lucky enough to have the mouse hit the nest?
Calculate the horizontal position of the mouse when it has fallen 12.0 m.
Solution:
- Reasoning:
We have motion with constant acceleration in two dimensions, or projectile
motion.
Given: x0, y0, vx0 = v0cosθ0,
vy0 = v0sinθ0, θ0 = -30o,
ay = -g.
Use vx = v0cosθ0 =
constant, x = x0 + v0cosθ0t,
vy = v0sinθ0 - gt,
y = y0 + v0sinθ0t - ½gt2.
Solve y - y0 = v0sinθ0t - ½gt2
for t, to find the time it takes the mouse to fall 12 m.
During this time the horizontal position of the mouse changes to x = x0 + v0cosθ0t.
- Details of the calculation:
(-12 m) = (-3.5 m/s)*0.5*t - 0.5*(9.8 m/s2)*t2.
t2 + (0.357 s)*t - 2.45 s2 = 0,
t = [-0.178 +(0.031 + 2.45)1/2]s = 1.4 s.
During this time the horizontal position of the mouse changes to x = x0 + v0cosθ0t,
x = -4 m * (3.5 m/s)*0.866*(1.4 s) = 0.23 m = 23 cm.
The center of the nest is at x = 0 and the nest has a radius of 15 cm. The
mouse misses the nest.
Problem:
Two projectiles are thrown with the same magnitude of initial velocity, one
at an angle of θ' with respect to the level ground and the other at an angle 90o
- θ'. Both projectiles will strike the ground at the same distance from
the projection point. Will both projectiles be in the air for the same time
interval?
Solution:
- Reasoning:
When two projectiles are thrown with the same initial speed and they have the
same range, then the one thrown with the smaller launch angle with respect to
the ground has the shorter flight time.
Note: We can denote the two launch angles that have the same range as θ0
= 45o ± θ, or as θ0 =
θ' and θ0 = 90o - θ'. The
relationship between θ and θ' is θ +
θ' = 45o.
Problem:
A ball is projected horizontally from the top of a building. One second
later, another ball is projected horizontally from the same point, with the same
velocity. At what point in the motion will the balls be closest to each other?
Will the first ball always be traveling faster than the second ball? What will
be the time difference between when the balls hit the ground? Can the
horizontal projection velocity of the second ball be changed, so that the balls
arrive at the ground at the same time?
Solution:
- Reasoning:
The horizontal distance between the balls will always be v0 times 1
s. After the second ball has been launched at t = 1 s, the vertical
distance (in meters) at time t (measured in seconds) will be ½g(t2
- (t -
1)2) = (4.9)(2t - 1). It increases with t, therefore during flight
the balls are closest to each other just after launch. (We do not know where
they were located before they were launched and what happens to them after they
land.) The horizontal component of velocity of both balls is constant. The
vertical component of velocity of ball 1 has magnitude gt and the vertical
component of velocity of ball 2 has magnitude g(t - 1). Since v2
= vx2
+ vy2,
ball 1 will always be faster than ball 2. Ball 2 will hit the ground 1 second
after ball 1, independent of the horizontal velocity component. The flight time
of each ball is determined by the vertical distance it must fall, not by the
horizontal velocity component.
Simultaneous motion
Some problems involve the motion of two particles. Often these problems
require that the two particles meet at the same place at the same time. An
often stated problem is the monkey problem.
A monkey is hanging from a branch in a tree, a certain height h above the
ground. A zookeeper stands a distance d from the tree, with a banana in
his hand. The zookeeper knows that the monkey always lets go of the branch
just as the banana is thrown to it. In which direction must the zookeeper
throw the banana, so that the monkey can catch it?
Analysis of the problem:
The position of a projectile as a function of time is given by
r = v0t
+ ½gt2.
We can view the motion of the projectile as a superposition of two motions, a motion with
constant velocity v0 in the initial direction and a downward motion with
constant acceleration, like the motion of a freely falling particle.
If the projectile is aimed
at the target and fired at t = 0, then motion with constant velocity
v0
will bring the projectile to the initial position of the target at some later time t.
In
the time interval between 0 and t the downward motion with constant acceleration carries
the projectile downward by an amount ½gt2. Superimposing the two motions
will bring the projectile at time t to the position of the freely falling target at time
t, independent of the magnitude of v0. In the time interval between
0 and t the freely falling target moves downward by an amount ½gt2.
Demos:
Ballistic cart
(Youtube)
Ball and cart have the same constant vx. The ball's and the
carts horizontal motions are the same. The ball's vertical motion is
independent of its horizontal motion and does not influence its horizontal
motion.
Shoot the target
(Youtube)
Without gravity, the arrow would hit the original position of the target.
With gravity, arrow and target accelerate downward at the same rate. (Youtube)
Module 3: Question 1
Consider projectile motion on level ground assuming negligible air resistance
and the initial angle being neither 0o nor 90o.
(a) Is the acceleration ever zero?
(b) Is the acceleration ever in the same direction as a component of
velocity?
(c) Is the acceleration ever opposite in direction to a component of
velocity?
Discuss this with your fellow students in the discussion forum!
Link:
Projectile Motion
For more information about projectile motion
please study this material from "the Physics Classroom".
- What is a Projectile?
- Characteristics of a Projectile's Trajectory
- Describing Projectiles with Numbers
- Horizontal and Vertical Components of Velocity
- Horizontal and Vertical Components of Displacement
- Initial Velocity Components
- Horizontally Launched Projectiles - Problem-Solving
- Non-Horizontally Launched Projectiles - Problem-Solving