An object moving in a circle of radius r
with constant speed v is accelerating. The
direction of its velocity vector is changing all the time, but the magnitude of
the velocity vector stays constant. The acceleration vector cannot have a
component in the direction of the velocity vector, since such a component would
cause a change in speed. The acceleration vector must therefore be
perpendicular to the velocity vector at any point on the circle. This
acceleration is called radial acceleration
or centripetal acceleration, and it points
towards the center of the circle. The magnitude of the centripetal
acceleration vector is ac = v2/r. (We skip the
derivation of this expression.)
Link:
Uniform circular Motion
Problem:
Describe how a driver can steer a car traveling at constant speed so that
(a) the acceleration is zero, or
(b) the magnitude of the acceleration remains constant.
Solution:
- Reasoning:
(a) The driver must make the car travel in a straight
line.
(b) The driver must make the car travel in a circle
(or in a straight line with a = 0).
Problem:
The orbit of the moon around
the earth is approximately circular, with a mean radius of 3.85*108
m. It takes 27.3 days for the moon to complete one revolution around the
earth. Find
(a) the mean orbital speed of the moon and
(b) its centripetal acceleration.
Solution:
- Reasoning:
The distance the moon travels in one orbital period T is d = 2πr.
Its speed is v = distance/time = d/T.
The centripetal acceleration of the moon is v2/r.
- Details of the calculation:
(a) The distance the moon travels in 27.3 days is d = 2πr = 2.41*109
m.
Its speed is v = d/(27.3 days) = (d/(2.36*106 s)) = 1023 m/s.
(b) The centripetal acceleration of the moon is v2/r =
2.725*10-3 m/s2.
Problem:
If the rotation of the earth increased so that the centripetal acceleration
was equal to the gravitational acceleration at the equator,
(a) what would be the tangential speed of a person standing at the equator, and
(b) how long would a day be?
Solution:
- Reasoning:
If the centripetal acceleration was equal to the gravitational acceleration
at the equator, then v2/r = g.
- Details of the calculation:
(a) The radius of the earth is 6368 km. We want v2/r
= 9.8 m/s2, or v2 = (9.8 m/s2)*6.368*106
m, or v = 7900 m/s.
(b) The length of a day would be t = 2πr/v = 5065 s =
84.4 min.
Non-uniform circular motion
A rollercoaster cart moving through a loop is changing speed as well as
direction of travel. Its acceleration has a radial component and a tangential
component, a = ar +
at. The
tangential component causes a change in speed and its magnitude is given by at
= dv/dt, and the radial component causes a change in direction and its
magnitude is given by ar = v2/r, where r is the radius of
curvature at the point in question. The components ar and
at are perpendicular to each other and the magnitude of
a
is a = (ar2 + at2)½.
Problem:
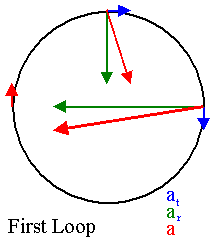 An ice skater is executing a figure eight, consisting of two equal tangent
circular paths. Throughout the first loop she increases her speed uniformly,
and during the second loop she moves at a constant speed. Make a sketch of her
acceleration vector at several points along the path of motion.
An ice skater is executing a figure eight, consisting of two equal tangent
circular paths. Throughout the first loop she increases her speed uniformly,
and during the second loop she moves at a constant speed. Make a sketch of her
acceleration vector at several points along the path of motion.
Solution:
- Reasoning:
Throughout the first loop the magnitude of the tangential acceleration at
is constant. The magnitude of the radial acceleration ar
increases as v2/r, as the speed of the skater increases as
v = att = (2atd)½, where d is the
distance traveled. When the skater starts out the acceleration vector is
tangential to the loop. But the angle θ it makes with a tangential line
increases as tanθ = ar/at = v2/(rat)
= 2d/r. Throughout the second loop at = 0 and ar is
constant, and the acceleration vector points towards the center of the loop.
Problem:
An automobile, the speed of which is increasing at a rate of 0.6 m/s2,
travels along a circular road of radius 20 m. When the instantaneous speed of
the automobile is 4 m/s, find
(a) the tangential acceleration component and
(b) the magnitude and direction of the total acceleration.
Solution:
- Reasoning:
The tangential acceleration of the car has a given, constant magnitude.
Its direction is tangential to the circle.
The radial acceleration has magnitude v2/r. Its direction
is perpendicular to the tangential acceleration and points towards the
center of the circle.
- Details of the calculation:
(a) The tangential acceleration of the car has a
constant magnitude of 0.6 m/s2.
(b) When
v = 4 m/s, the radial acceleration has magnitude ar = v2/r = (16 m/s2)/(20
m) = 0.8 m/s2, a = (ar2 + at2)½
= 1 m/s2.
Let θ be the angle the acceleration vector makes with the line pointing from
the position of the car towards the center of the circle. Then tanθ = at/ar
= 0.75, θ = 36.9o.
Problem:
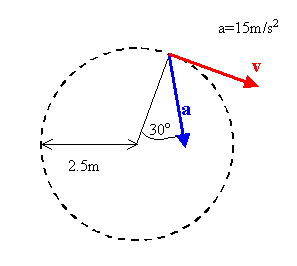 The figure on the right represents the total acceleration of a particle moving
clockwise in a circle of radius 2.5 m at a given instant of time. At this
instant, find
The figure on the right represents the total acceleration of a particle moving
clockwise in a circle of radius 2.5 m at a given instant of time. At this
instant, find
(a) the centripetal acceleration,
(b) the speed of the particle, and
(c) its tangential acceleration.
Solution:
- Reasoning:
We have to find the component of the vector a.
- Details of the calculation
(a) ar = a cos(30o) = 12.99 m/s2.
(b) ar
= v2/r, v2 =
rar, v = 5.7 m/s.
(c) at = a sin(30o) = 7.5 m/s2.
Module 3: Question 2
Can centripetal acceleration change the speed of circular motion?
Discuss this with your fellow students in the discussion forum!
Common units for angles are degrees and radians. We
have 360o = 2π radians. The circumference of a circle of radius r is
2πr. The length of a circular arc subtaining 180o is πr. The length
of an arc subtaining 90o is (π/2)r. We see that the length of a
circular arc subtaining an angle θ is θr, where θ is measured in radians.
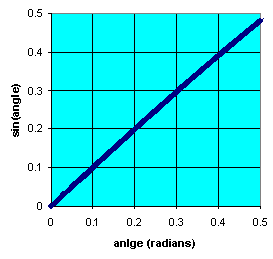
For small angles θ, sinθ ~ θ, if θ
is measured in radians. You can verify this looking at the table or the graph.
| angle (deg) |
angle (rad) |
sin(angle) |
| 0 |
0 |
0 |
|
0.1 |
0.001745 |
0.001745 |
| 0.2 |
0.003491 |
0.003491 |
| 0.3 |
0.005236 |
0.005236 |
| 0.4 |
0.006981 |
0.006981 |
| 0.5 |
0.008727 |
0.008727 |
| 0.6 |
0.010472 |
0.010472 |
| 0.7 |
0.012217 |
0.012217 |
| 0.8 |
0.013963 |
0.013962 |
| 0.9 |
0.015708 |
0.015707 |
| 1 |
0.017453 |
0.017452 |
 An ice skater is executing a figure eight, consisting of two equal tangent
circular paths. Throughout the first loop she increases her speed uniformly,
and during the second loop she moves at a constant speed. Make a sketch of her
acceleration vector at several points along the path of motion.
An ice skater is executing a figure eight, consisting of two equal tangent
circular paths. Throughout the first loop she increases her speed uniformly,
and during the second loop she moves at a constant speed. Make a sketch of her
acceleration vector at several points along the path of motion. The figure on the right represents the total acceleration of a particle moving
clockwise in a circle of radius 2.5 m at a given instant of time. At this
instant, find
The figure on the right represents the total acceleration of a particle moving
clockwise in a circle of radius 2.5 m at a given instant of time. At this
instant, find