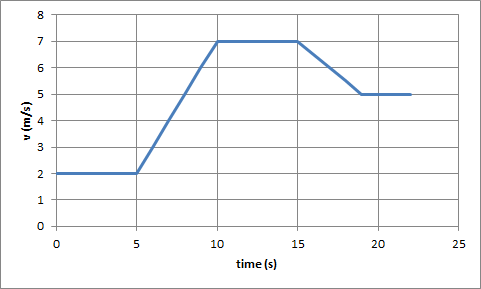
(a) What is the net force acting on the particle at t = 6 s?
(b) What is the net force acting on the particle at t = 12 s?
(c) What is the net force acting on the particle at t = 16 s?
Let us assume that our reference frame is an inertial frame. What happens in an inertial frame when an object is acted of by a net force? Newton's second and third law answer this question.
Newton's second and third law are valid in all inertial reference frames.
Newton's second law states that the acceleration of an object is directly proportional to the net force acting on it, and inversely proportional to its mass.
Unbalanced forces cause acceleration.
no net force <--> no acceleration
The net force is the vector sum of all forces acting on the object.
F = ∑iFi, Fx = ∑iFix, Fy = ∑iFiy, Fz = ∑iFiz,
In algebraic form we write Newton's second law as F = ma.
This is a vector equation. It is equivalent to the three equations, Fx = max, Fy = may, Fz = maz. The acceleration a = F/m is in the direction of the force and proportional to the magnitude of the force. The mass of an object is a measure of its inertia, its resistance to changing its state of motion. If two objects are supposed to have the same acceleration, then the more massive object must be acted on by a larger force, while the less massive object must be acted on by a smaller force. The mass is a scalar quantity.
Units: In SI units, mass is
measured in kg, acceleration in m/s2 and force in Newton (N). 1 N = 1 kg·m/s2.
In the British engineering system the unit of force is the pound (lb).
(Conversion: 1 pound-force = 4.448 N)
Given the same push or pull, larger masses accelerate less than smaller masses. You need much less force to accelerate a tricycle than to accelerate a car. Because of its inertia, you need a force to accelerate an object. If there is no net force acting on an object, it will not accelerate, its velocity will not change. If it is initially at rest, it will stay at rest, if it is moving with a given speed in a certain direction, it will keep on moving with the same speed in the same direction.
Link: The Truck and the Ladder
A net force F, applied to an object of mass m1, produces
an acceleration of 3 m/s2. The same force, applied to a second
object of mass m2 produces an acceleration of 1 m/s2.
(a) What is the value of the ratio m1/m2?
(b) If m1 and m2 are combined, find their
acceleration under the action of the force F.
Solution:
A car with a mass of 850 kg is moving to the right with a constant speed of
1.44 m/s.
(a) What is the total force on the car?
(b) What is the total force on the car if it is moving to the left with a
constant speed of 1.44 m/s.
Solution:
A plot of velocity versus time for a m = 0.1
kg particle moving along the x-axis starting at the origin is shown below.
(a) What is the net force acting on the particle at t = 6 s?
(b) What is the net force acting on the particle at t = 12 s?
(c) What is the net force acting on the particle at t = 16 s?

Solution:
A 3 kg mass undergoes an acceleration given by a = (2i + 5j) m/s2. Find the resultant force F and its magnitude.
Solution:
A heavy freight train has a mass of 15000 metric tons. If the locomotive can exert a pulling force of 750000 N, how long does it take to increase the speed from 0 to 80 km/h?
Solution:
Suppose a truck loaded with sand accelerates at 0.5 m/s2 on a highway. If the driving force on the truck remains constant, what happens to the truck's acceleration, if its trailer leaks sand at a constant rate through a hole in its bottom?
Solution: