

Consider the following situations:
What is happening is a consequence of Newton's third law.
For every force that an
object exerts on a second object, there is a force equal in magnitude but
opposite in direction exerted by the second object on the first object.
Forces are the result of interactions.
You pull on me, I pull on you. If no other forces are present, I will accelerate towards you. My acceleration has
the magnitude of the force divided by my mass. You will accelerate
towards me. Your acceleration has the magnitude of the force divided by
your mass.
You push against the table, the table pushes against you. You accelerate away from the table. Why is the table not accelerating away from you?
Standing on a very slippery surface or on a skateboard, you throw a heavy object away from you in a northerly direction. To do this, you have to exert a force on the object in the northerly direction. The object exerts a force on you, which has equal magnitude but points towards the south. You accelerate southward.
Newton's third law is also called the law of action and reaction. For every action force, there exists a reaction force, equal in magnitude and opposite in direction. The objects interact.
The action and reaction force always act on different objects.
Two forces acting on the same object, even if they have the same
magnitude and point in opposite direction, never form an action-reaction pair.
An apple with a 0.2 kg mass sits on a table in equilibrium.
(a) What forces act on it? Provide their magnitude and direction.
(b) What is the reaction force to each of the forces acting on the apple?
(c) What are the action-reaction pairs?
Solution:
While a football is in flight, what forces act on it? What are the action and reaction pairs while the football is being kicked and while it is in flight?
Solution:
Action-reaction pairs are forces of equal magnitude and opposite direction that act on different object. They never act on the same object.
Newton's 3rd law tells us that forces are interactions. An object cannot exert a force on another object without feeling a reaction force itself. T he reaction force has the same magnitude and points in the opposite direction as the force the object exerts on the other object. What and object does as a result of being acted on by a reaction force depends not only on the reaction force but on the net force acting on the object. The net force is the sum of the reaction force and all the other forces acting on the object.
A device used since the 1940s to measure the kick or recoil of the body due to heart beats is the "ballistocardiograph" . What physics principle(s) are involved here to measure the force of cardiac contraction? How might we construct such a device?
Discuss this with your fellow students in the discussion forum!
Suppose that you are holding a cup of coffee in your hand. Identify all forces on the cup and the reaction to each force.
Discuss this with your fellow students in the discussion forum!
Newton's second law: Fnet = ma
To find the net force on an object, all the vector forces that act on the object have to be added. We use free-body diagrams to help us with this task. Free-body diagrams are diagrams used to show the relative magnitude and direction of all forces acting on an object in a given situation. The object is represented by a box or some other simple shape. The forces are represented by arrows. The length of the arrow in a free-body diagram is proportional the magnitude of the force. The direction of the arrow gives the direction of the force. Each force arrow in the diagram is labeled. All forces, which act on the object, must be represented in the free-body diagram. A free body diagram only includes the forces that act on the object, not the forces the object itself exerts on other objects.
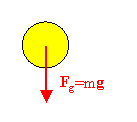 Example:
Example:A free-body diagram for a freely falling ball:
Neglecting air friction, the only force acting on the ball is gravity.
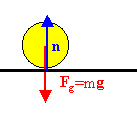 Example:
Example:A free-body diagram for a ball resting on the ground:
Gravity is acting downward. The ball is at rest. The ground must exert
a force equal in magnitude and opposite in direction on the ball. This
force is called the normal force, n, since it is normal to the surface.
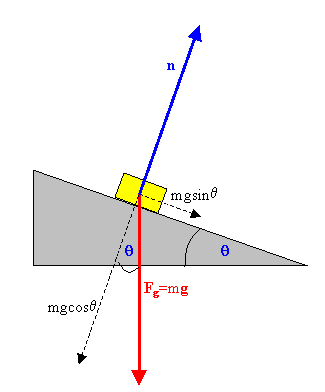 Example:
Example:A free-body diagram for a mass on an inclined plane:
Gravity acts downward. The component of
Fg
perpendicular to the surface is cancelled out by the normal force the
surface exerts on the mass. The mass does not accelerate in the
direction perpendicular to the surface. The component of Fg
parallel to the surface causes the mass to accelerate in that direction.
Assume two opposing teams and an opposing team are pulling on a rope in opposite directions. is there a net force on the rope?
If the rope is accelerating in the direction of one of the teams, then there
is a non-zero net force. F = ma. The net force is the vector sum of the force of gravity and the forces
exerted by the two teams.
The opposing team, since the rope starts accelerating in their
direction.
If the rope is not accelerating, even so each team is pulling as hard as it
can then there is no net force acting on the rope. However, there is tension in the
rope. Tension results from different forces acting on different parts of
the body. Tension can break things. A pure force, i.e. the same force
acting on all parts of the body, cannot break things.
If instead of
pulling on the rope the two teams push on a heavy rock, but the rock does
not move, then again the net force on the rock is zero. However, now the
rock is under compression.
The tension T is a scalar. It is defined as the magnitude of the force with which the stretched rope pulls on whatever it is attached to. This force is often denoted by T. The direction of T depends on which end of the rope is being considered.
The net force acting on an object is always the vector sum of all forces acting on an object. The object's acceleration is in the direction of this net force and has magnitude a = (net force/object's mass).
A 15-lb block rests on the floor. (Note: lb is a
unit of force, the weight of the block is 15 lb.)
(a) What
force does the floor exert on the block?
(b) If a rope is tied to
the block and run vertically over a pulley and the other end is attached to
a free-hanging 10-lb weight, what is the force exerted by the floor on the
15-lb block?
(c) If we replace the 10-lb weight in part (b) with a
20-lb weight, what is the force exerted by the floor on the 15-lb block?
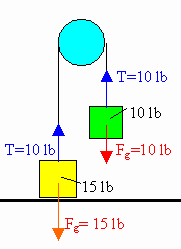
Solution:
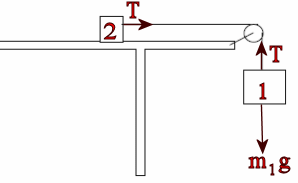 Two
blocks, one sitting on a table and the other heavier one hanging over its edge,
are connected by a light string as shown in the figure. Which force
makes the block on the table accelerate, the tension in the string or the weight of
the hanging block? Write down an expression for the acceleration a.
Two
blocks, one sitting on a table and the other heavier one hanging over its edge,
are connected by a light string as shown in the figure. Which force
makes the block on the table accelerate, the tension in the string or the weight of
the hanging block? Write down an expression for the acceleration a.
Solution:
(a) Find the tension in each of the cords of the system shown in the figure below. Neglect the masses of the cords.
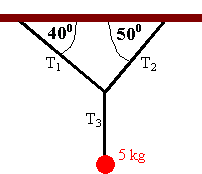
(b) Find the tension in each of the cords of the system shown in the figure below. Neglect the masses of the cords.
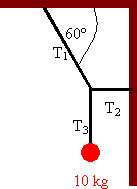
Solution: