Review:

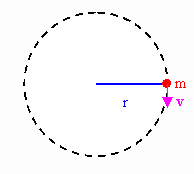
An object moving in a circle of radius r with constant speed v is accelerating.  The direction of its velocity vector is changing all the time, but the magnitude of the velocity vector stays constant.  The acceleration vector cannot have a component in the direction of the velocity vector, since such a component would cause a change in speed.  The acceleration vector must therefore be perpendicular to the velocity vector at any point on the circle.  This acceleration is called radial acceleration or centripetal acceleration, and it points towards the center of the circle.  The magnitude of the centripetal acceleration vector is a_c = v²/r.

Under different circumstances, what is the force?

Let us solve some problems investigating this question.

Problem:

A 3 kg mass attached to a light string rotates on a horizontal frictionless table.  The radius of the circle is 0.8 m and the string can support a mass of 25 kg before breaking.  What range of speeds can the mass have before the string breaks?

Solution:

• Reasoning:
  A mass attached to a string rotates on a horizontal, frictionless table.
  We assume that the mass rotates with uniform speed.  It is accelerating.  The direction of the acceleration is towards the center of the circle, and its magnitude is v²/r.  There is tension in the string.  The string pulls on the mass with a force F directed towards the center of the circle.  This force F is responsible for the centripetal acceleration, F = mv²/r.
  The string can support a mass of 25 kg before breaking, i.e. we can let a mass of up to 25 kg hang from the string near the surface of the earth.  The maximum tension in the string therefore is F_max = mg = (25 kg)(9.8 m/s²) = 245 N.
  Given F_max = 245 N and F = mv²/r, we can find v_max.
• Details of the calculation:
  v_max² = F_maxr/m = (250 N)(0.8 m)/(3kg).  v_max = 8.1 m/s.

Problem:

A coin placed 30 cm from the center of a rotating, horizontal turntable slips when its speed is 50 cm/s.
(a)  What force provides the centripetal acceleration when coin is stationary relative to the turntable?
(b)  What is the coefficient of static friction between coin and turntable?

Solution:

• Reasoning:
  When the coin is at rest relative to the rotating turntable, the force of static friction between the coin and the turntable provides the centripetal acceleration.
  The force of static friction has a maximum value f_s = μ_sN = μ_smg.
  Setting μ_smg = mv²/r, we can solve for μ_s.
• Details of the calculation:
  (a)  The force of static friction between the coin and the turntable provides the centripetal acceleration.
  (b)  The magnitude of the maximum force of static friction is f_s = μ_sN.  This maximum force of static friction is equal to mv²/r when v = 0.5 m/s.  We have μ_sN = μ_smg = mv²/r,
  or μ_s = v²/(rg) = (0.5m/s)²/(0.3m 9.8m/s²) = 0.085.

Problem:

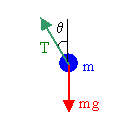
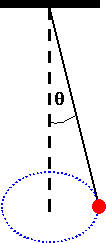Consider a conical pendulum with a 80 kg bob on a 10 m wire making an angle of θ = 5^o with the vertical.  Determine
(a)  the horizontal and vertical component of the force exerted by the wire on the pendulum and
(b)  the centripetal acceleration of the bob.

Solution:

• Reasoning:
  A free-body diagram of the bob is shown on the right.
  The bob does not change its vertical position, y = constant, v_y = a_y = 0.  The vertical component of T must have magnitude mg.
  The horizontal component of T provides the centripetal (radial) acceleration a_r.
• Details of the calculation:
  (a)  The vertical component of T must have magnitude mg.
  Tcos(5^o) = mg,  T = (80 kg 9.8 m/s²)/cos(5^o) = 787 N
  The magnitude of horizontal component of T is Tsin(5^o) = 68.6 N.  The horizontal component of the force points towards the center of the circle.
  
  (b)  Tsin(5^o) = ma_r, a_r = (68.6 N)/(80 kg) = 0.857 m/s².
  The speed of the bob is found from a_r = v²/r, v = (a_rr)^½.
  Since r = (10 m)*sin(5^o), we have v = 0.86 m/s.

Problem:

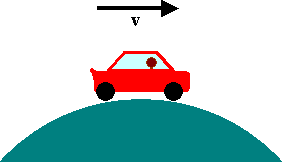An 1800 kg car passes over a hump in a road that follows the arc of a circle of radius 42 m.
(a) What force does the road exert on the car as the car passes the highest point of the hump if the car travels at 16 m/s?
(b) What is the maximum speed the car can have as it passes this hump before losing contact with the road?

Solution:

• Reasoning:
   A free- body diagram of the car is shown.
  

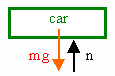
  The only forces acting on the car moving with constant speed are gravity and the normal force, which is exerted by the road.  If these forces are equal in magnitude, the car does not accelerate.  If the car is moving on a circular arc, then it is accelerating.  The acceleration is a_r = v²/r.  The gravitational force must therefore have a larger magnitude than the normal force.

• Details of the calculation:
  We need
  mg - n = mv²/r, or n = m(g - v²/r).
  n = (1800 kg)(9.8 m/s² - (16 m/s)²/(42 m)) = 6669 N
  
  (b) The car looses contact with the road when n becomes zero.  Then the road does no longer support the car.  This happens when g - v²/r = 0, or v² = gr = 411.6 m²/s², v = 20.3 m/s.

Module 5: Question 1

Do you feel yourself thrown to either side when you negotiate a curve that is ideally banked for your car's speed? What is the direction of the force exerted on you by the car seat?

Discuss this with your fellow students in the discussion forum!

Gravity

Massive objects have inertia.  It takes a force to change their state of motion.  All massive object interact via the gravitation force.  A particle with mass m₁ exerts a force F₁₂ on a particle with mass m₂.  Newton's law of gravitation gives this force as

F₁₂ = (-G m₁m₂/r₁₂²) (r₁₂/r₁₂).
Here r₁₂ is the distance between particles 1 and 2,  and (r₁₂/r₁₂) is the unit vector pointing from particle 1 to particle 2. 
G is the gravitational constant, G = 6.67*10^-11 Nm²/kg².

The force F₂₁, which the particle with mass m₂ exerts on the particle with mass m₁, is equal to -F₁₂, according to Newton's third law.  The gravitational force is always attractive.

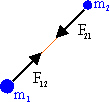The point in an object from which the distance r₁₂ is measured is its center of mass.  Mass m₁ pulls on mass m₂, and mass m₂ pulls on mass m₁.  The center of mass of each object is pulled towards the center of mass of the other object.

Weighing the earth

The radius of the earth is R = 6368 km.  If you climb a 1000 m high mountain, your distance from the center of the earth changes by (1/6368)*100 % = 0.016 % and the magnitude of the gravitational force acting on you changes by (1/6368)²*100 % = 2.4*10^-6 %.  For all objects near the surface of the earth the distance from the center is nearly constant, and the magnitude of the gravitational force vector is therefore approximately constant.  Over small distances, when the curvature of the earth's surface can be neglected, the direction of the gravitational force vector is also nearly constant.  It points straight downward towards the center of the earth.
The force of gravity on an object of mass m on the surface of the earth has magnitude F = mg.  Using Newton's law of gravity we write GMm/R² = mg, where M is the mass of the earth.  We therefore have M = gR²/G.
Using R = 6.4*10⁶ m, we find M = (9.8 m/s²)(6.4*10⁶ m)²/(6.67*10^-11 Nm²/kg²) = 6*10²⁴ kg.

Orbiting

The gravitational attraction between an object and the earth pulls the object towards the center of the earth.  When an object circles the earth, the direction of the gravitational force on the object constantly changes.  The radius of the earth is so large, that the earth appears locally flat to an observer standing on the surface.  When a problem involves only distances which are much smaller than the radius of the earth we often neglect the curvature of the earth's surface and assume that the gravitational force points in the same downward direction everywhere.

Link:  The satellite as a projectile

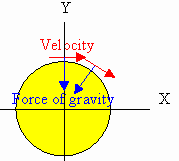Assume that near the surface of the earth an object is thrown in the x-direction as shown in the figure above.  Initially it accelerates only in the y-direction.  But as the object moves, the direction of the acceleration changes.  If the objects initial speed is high enough, we have to take the change in the direction of the force into account when calculating the objects trajectory.  An object in a circular orbit around the earth is constantly falling towards the center of the earth.  It is constantly accelerating.  But while it moves on a curved trajectory, the surface of the earth curves away from the object so that the distance between the earth and the object stays constant.

The force of gravity always points towards the center of the object's circular orbit and is responsible for the centripetal acceleration of the object.

F = mv²/r

For an object near the surface of the earth F = mg and r = 6.4*10⁶ m.  The speed of the orbiting object is found from mg = mv²/r, v² = gr = (9.8 m/s²)(6.4*10⁶ m).  We have v = 7919 m/s, or approximately 8000 m/s.  It takes the object t = 2πr/v = (6.28*6.4*10⁶ m)/(7919 m/s) = 5075 s = 84 min to complete an orbit.

If the same object moved in a circular orbit with a larger radius, the force of gravity on the object would be smaller.  As we double the distance from the center of the earth the force of gravity decreases by a factor of 1/4.  The centripetal acceleration v²/r decreases by a factor of 1/4.  This means that v² must decrease by a factor of ½.  We have v = 5600 m/s and it take 14355 s = 240 min to complete an orbit.

Objects in geo-synchronous orbits complete an orbit in 24 hours or 86400 s.  Their speed is therefore is v = 2πr/(86400 s).  Writing GMm/r² = mv²/r = m(2πr/(86400 s))²/r, or r³ = GM(86400s)²/(4π). we can solve this equation for the radius of the geo-synchronous orbit.  With M = 6*10²⁴ kg we have r = 42260 km.  A geo-synchronous satellite orbits about 42260 km - 6400 km = 35860 km above the surface of the earth.  The radius of its orbit is 6.6 times the radius of the earth.

The moon orbits the earth once every 27.3 days.  We can find the distance to the moon in the same way we found the distance to a geo-synchronous satellite.  The earth-moon distance is 384400 km.

Problem:

When a falling meteor is a distance above the earth's surface of 3 times the Earth's radius, what is its free-fall acceleration due to the gravitational force exerted on it?

Solution:

• Reasoning:
  The force on the meteor is F = ma = GMm/r².  Therefore a = GM/r².
• Details of the calculation:
  a = GM/r², a = (6.67*10^-11 Nm²/kg²)*(6*10²⁴ kg)/(4*6.4*10⁶ m)² = 0.61 m/s².
  (The meteor is 3 earth radii above the earth surface, so it is 4 earth radii from its center.)

For more information about uniform circular motion motion, study this material from "the Physics Classroom".

Link:  Motion Characteristics for Circular Motion

1. Speed and Velocity
2. Acceleration
3. The Centripetal Force Requirement
4. The Forbidden F-Word
5. Mathematics of Circular Motion

Link:  Applications of Circular Motion

1. Newton's Second law - Revisited
2. Amusement Park Physics
3. Athletics