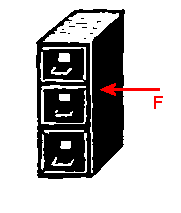
Suppose that you want to move a heavy file cabinet, which is standing in the middle of your office, into a corner.  You push on it, but nothing happens.  What is going on?
You exert a force, but there is no acceleration.  The net force must be zero.
Which force of equal magnitude points in a direction opposite to the direction of the force you are applying?

The force of static friction (f_s) cancels the applied force when the cabinet is at rest while you are pushing on it.

You push harder.  Eventually the cabinet breaks away and starts accelerating.  But you have to keep on pushing just to keep it moving with a constant velocity.  When you stop pushing, it quickly slows down and comes to rest.  Why?

While the cabinet is moving the force of kinetic friction (f_k) opposes the applied force.  When it is moving with constant velocity, the two forces exactly cancel.

Where do these frictional forces come from?  Frictional forces are intermolecular forces.  These forces act between the molecules of two different surfaces that are in close contact with each other.  On a microscopic scale, most surfaces are rough.  Even surfaces that look perfectly smooth to the naked eye show many projections and dents under a microscope.  The intermolecular forces are strongest where these projections and dents interlock resulting in close contact.  The component of the intermolecular force normal to the surfaces provides the normal force which prevents objects from passing through each other and the component parallel to the surface is responsible for the frictional force.

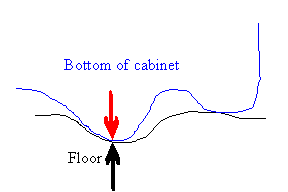Assume a cabinet is resting on the floor.  Nobody is pushing on it.  The net intermolecular force between the molecules of two different surfaces is normal to the surface.   The force of gravity acting on the cabinet (red arrow) is balanced by the normal force from the floor acting on it (black arrow).

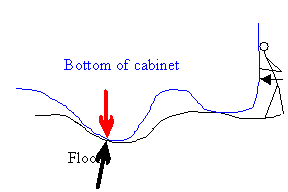Now assume that you are pushing against the cabinet.  The cabinet is not moving, but the surface molecules are displaced by microscopic amounts.  This results in a net intermolecular force which has a component tangential to the surface (the force of static friction).  This tangential component opposes the applied force.  The net force on the cabinet is zero.  The harder you push the greater is the microscopic displacement of the surface molecules and the greater is the tangential component of the net intermolecular force.

When you push hard enough, some of the projections on the surfaces will break off, i.e. some of the surface molecules will be completely displaced.  The horizontal component of the net intermolecular force diminishes and no longer completely opposes the applied force.  The cabinet accelerates.  But while the horizontal component has diminished, it has not vanished.  It is now called the force of kinetic friction.  For the cabinet to keep accelerating, you have to push with a force greater in magnitude than the force of kinetic friction.  To keep it going with constant velocity you have to push with a force equal in magnitude to the force of kinetic friction.  If you stop pushing, the force of kinetic friction will produce an acceleration in the opposite direction of the velocity, and the cabinet will slow down and stop.

The frictional force always acts between two surfaces, and opposes the relative motion of the two surfaces.

The maximum force of static friction between two surfaces is roughly proportional to the magnitude of the force pressing the two surfaces together.  The proportional constant is called the coefficient of static friction μ_s.  The magnitude of the force of static friction is always smaller than or equal to μ_sN,   We write f_s ≤ μ_sN, where f_s is the magnitude of the frictional force and N is the magnitude of the force pressing the surfaces together.  For the cabinet and the floor, N is the weight of the cabinet.  The coefficient of static friction is a number (no units).  The rougher the surface, the greater is the coefficient of static friction.

As long as the applied force has a magnitude smaller than μ_sN, the force of static friction f_s has the same magnitude as the applied force, but points in the opposite direction.

The magnitude of the force of kinetic friction acting on an object is f_k = μ_kN, where μ_k is the coefficient of kinetic friction.  For most surfaces, μ_k is less than μ_s.

This short video clip illustrates the difference between static and kinetic friction.

Problem:

A racing car accelerates uniformly from 0 to 80 mi/h in 8 s.  The magnitude of the force that accelerates the car is approximately equal to the magnitude of the frictional force between the tires and the road.  If the tires do not spin, determine the minimum coefficient of static friction between the tires and the road.

Solution:

• Reasoning:
  The magnitude of the force accelerating the car is F = ma.  We assume that the static frictional force f_s has the same magnitude.
  f_s = ma = μ_s(min)N.  The normal force is N = mg and μ_s(min) is the minimum required coefficient of static friction.
• Details of the calculation:
  The magnitude of the acceleration is a = (80 mile/h)/(8 s) = (35.76 m/s)/(8 s) = 4.47 m/s².
  The magnitude of the force accelerating the car is f_s = ma = μ_s(min)N = μ_s(min)mg.
  We therefore have a = μ_s(min)g,  μ_s(min) = a/g = 4.47/9.8 = 0.46.

Problem:

A woman at an airport is towing her 20 kg suitcase at constant speed by pulling on a strap at an angle of θ above the horizontal.  She pulls on the strap with a 35 N force, and the frictional force on the suitcase is 20 N.
(a)  Draw a free body diagram of the suitcase.
(b)  What angle does the strap make with the horizontal?
(c)  What normal force does the ground exert on the suitcase?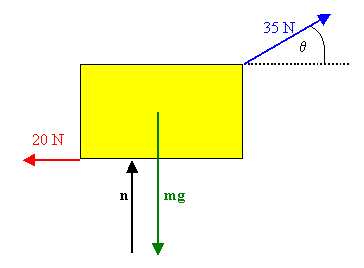

Solution:

• Reasoning:
  constant velocity <--> no acceleration <--> no net force
  The x- and y-components of all forces have to add up to zero.
  To keep track of all the forces, it helps to draw a free-body diagram.
• Details of the calculation:
  (a)  See the drawing on the right.
  (b)  The suitcase moves with constant velocity, the net force on the suitcase is zero.
  F_x = 0 implies (35 N)cosθ = 20 N, or cosθ = 20/35, θ = cos^-1(20/35) = 55.15^o.
  (c)  F_y = 0 implies mg = n + (35 N)sinθ,  (20 kg)(9.8 m/s²) = n + (35 N)0.82,
  n = 167.3 N.

Problem:

Determine the stopping distance for a skier with a speed of 20 m/s on a slope that makes an angle θ with the horizontal.  Assume μ_k = 0.18 and θ = 5^o.

Solution:

• Reasoning:
  Draw a free-body diagram.
  The component of the net force perpendicular to the slope must be zero.
  The normal force must cancel the perpendicular component of gravity.
  Therefore the magnitude of the normal force n = mg cosθ.
  The magnitude of the frictional force is proportional to the normal force, f_k = μ_kmg cosθ.
  The component of the net force down the slope is F = mg sinθ - μ_kmg cosθ.
  It is the vector sum of the frictional force and the tangential component of gravity.
  The acceleration down the slope produced by this net force is a F/m = g sinθ - μ_kg cosθ.
• Details of the calculation:
  μ_kg cosθ = 0.18 (9.8 m/s²) cos(5^o) = 1.76 m/s².
  g sinθ = (9.8 m/s²) sin(5^o) = 0.85 m/s².
  a = g sinθ - μ_kg cosθ = -0.91 m/s²
  The acceleration points up the slope, in a direction opposite to the velocity.
  The acceleration is constant.  We now can use kinematic equations to solve for the stopping distance.
  We have 0 - v₀ = -at, t = v₀/a = (20/0.91) s = 21.98 s for the time it takes the skier to come to a stop.
  In this time he travels a distance s = v₀t - ½at².  s = 219.8 m.

Link:  Solving inclined plane problems (Youtube)

Problem:

Suppose you are driving a car along a highway at a high speed.  Why should you avoid slamming on your brakes if you want to stop in the shortest distance?  That is, why should you keep the wheels turning as you brake?

Solution:

• Reasoning
  When the wheels are turning, friction between the surfaces of the brake pads and the disks or drums of the wheels is responsible for decelerating the car.  When the wheels are locked, friction between the tires and the road decelerates the car.  The brake pads are designed for the job, and the coefficient of kinetic friction between the brake pads and the disk or drum is large.

Problem:

A heavy box sits in the back of a pickup truck. The truck and the box are accelerating towards the left.  What is the direction of the frictional force on the box?

Solution:

• Reasoning:
  The box accelerates towards the left.  The only force with a horizontal component acting on the box is friction.  The direction of the frictional force on the box is towards the left.  Friction accelerates the box towards the left and prevents the relative motion of the box and the bed of the truck.  (Without friction the truck would just pull away from the box.)  A frictional force of equal magnitude pointing in the opposite direction acts on the truck.  The truck therefore accelerates at a lower rate than it would if the box was not present.