RollingConsider a point object, i.e. for the moment let us neglect any possible rotation of the object. If this object is at rest and the net force acting on the object is zero, the object is at an equilibrium position. If, when slightly disturbed, the object is acted on by a restoring force pointing to its equilibrium position, it is said to be in stable equilibrium. Objects suspended on springs are in stable equilibrium. An object sitting on top of a ball, on the other hand, is in unstable equilibrium. When disturbed, it is acted on by a force pointing away from the equilibrium position.
A ball and a bowl
(a) The ball is in stable equilibrium at the bottom of a bowl.
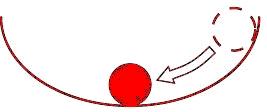
(b) The ball is in unstable equilibrium at the top of a bowl.
The force of static friction does no work on an object at rest and you do no work against this force. Even though you may be pushing hard against an object acted on by the force of static friction, the object is not moving. The displacement is zero and W = 0.
You, however, do work against the force of sliding or kinetic friction. If you push with force F on a cabinet, while the cabinet moves with constant velocity through a distance d in the direction of F, the work you do on the cabinet is W = Fd = μNd. The force of kinetic fiction does negative work W = -μNd on the cabinet.
Work is the conversion of one form of energy into another. You do positive work on the cabinet, but the cabinet is not gaining potential energy, (it is not being pushed up a hill), and it is not gaining kinetic energy (it is moving with constant speed). The work done by the frictional force (negative work) on the cabinet transforms the energy you transfer to the object into disordered energy. Sliding friction converts most of the work you do on the file cabinet into thermal energy. As you slide the cabinet across the floor, the bottom of the cabinet and the floor get warmer. This thermal energy cannot easily be converted back into ordered energy, it cannot easily be used to do useful work.
Sliding friction also causes wear. Some of the work you do on the file cabinet is converted into electrostatic potential energy. The atoms and molecules in a solid object are held together by electrical forces, and you have to do work to break them apart. To detach a cluster of atoms from the bottom of the file cabinet you must do work against the electrostatic force, in the same way you must do work against the gravitational force to lift a rock up from the ground. As you slide your cabinet across the floor, some material is removed from the bottom of the cabinet and from the floor. It will not take long before damage becomes visible.
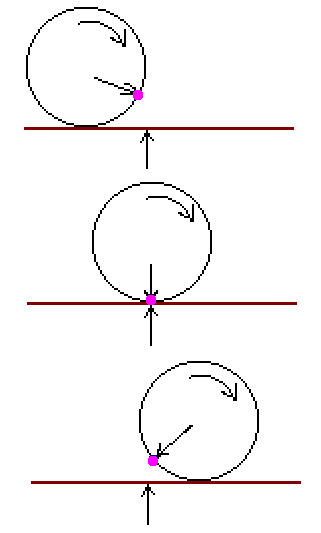
RollingIf you put your file cabinet on a small cart with wheels, you can greatly reduce the force you need to apply to move the cabinet with constant speed. Wheels do not slide across the floor, they roll across the floor. At any instant only a very small portion of the surface of a wheel is in contact with the floor. Static friction prevents this portion from sliding. As the wheel rolls, a new portion of the wheel is lowered onto the floor, while the portion previously in contact with the floor is raised. Pure rolling involves only static friction, not kinetic friction.
The figure on the right tracks a spot on the rim of a rolling wheel. The spot makes contact with the floor at only one point, pointed to by the arrow.
A cart on wheels can roll across the floor. Rolling does not involve the production of thermal energy. However, to attach two wheels to the cart, you need an axle. A smooth bearing lets the axle slide inside the hub of the wheel. The force of sliding friction converts some of the kinetic energy of the system into heat. However, the surfaces of the bearing are usually very smooth and the hub has a small radius, so that the total amount of work done against frictional forces is small. Adequate lubrication can reduce it even further.
You get in your car, start the engine, put it into "drive", step on the accelerator, and accelerate.
What makes the car start moving forward?
Let us, for the moment, forget about the details of the engine and the transmission. The car contains all the hardware necessary to make the wheels turn. If a forklift lifts the car so that the wheels do not touch the ground and you get in the car, start the engine, put it into "drive", and step on the accelerator, then the wheels start turning. The car, however, does not start moving forward.
What is missing?
Without frictional forces your car will not accelerate. If you are parked on an icy surface or your car is stuck in mud, the wheels will turn, but your car does not accelerate. The center of mass of a system acted on only by internal forces cannot accelerate. This is a consequence of Newton's third law. We need an external force to accelerate the car, and that force is friction.
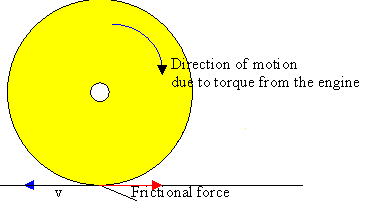How does friction accelerate your car?
Assume you want the car to accelerate towards the right. When a wheel is
spinning, the contact point with the ground is moving towards the
left. The direction of the frictional force on the portion of the wheel
contacting the ground is opposite to the direction of the velocity of this
portion of the wheel with respect to the ground. When
a wheel is rolling the contact point is not sliding at all. When
a rolling wheel is accelerating,
internal forces try to accelerate the contact point
backward. The force of static friction now is
directed towards the right and it cancels those forces. Neglecting
drag, the force of static friction is the only external force acting on the
car in the horizontal direction, and without it there would be no net force to
accelerate the car.
How can the force of static friction be responsible for accelerating the car
and do no work? Internal forces between different parts of the car in
the engine, transmission, etc, come in action-reaction pairs. These
forces can do work. The frictional force can cancel one of the forces of an action-reaction pair with a direction opposite to the direction of the
acceleration, leaving a net force in the direction of the acceleration.
Assume you are dropping a ball onto a perfectly hard floor. It will rebound, but even the "liveliest " ball will not rise back to its starting position.
Why does it bounce back, and why does it loose height on the rebound?
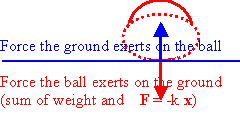The ball behaves like a spherical spring. When the ball hits the floor it exerts a
force on the floor larger than its weight, and the floor exerts a force on the
ball of equal magnitude. This force and the gravitational force acting on
the ball compress the ball. As long as the compression is small, Hooke's law is satisfied, the force compressing the ball is
proportional to the displacement of the ball from its equilibrium shape. The gravitational potential energy the ball has before it is dropped is
converted into kinetic energy while the ball is falling and then into elastic potential
energy when the ball is compressed. But because the material the
ball is made of is not perfectly elastic, internal friction converts some of the energy
into thermal energy. The elastic potential energy stored in the ball when it has lost all its kinetic energy
is converted back into kinetic and gravitational potential energy. The thermal energy,
however, is not converted back.
The ball on the floor acts like a compressed spring. It pushes on the floor with a force proportional to its displacement from its equilibrium shape. The floor pushes back with a force of equal magnitude in the upward direction. This force is greater in magnitude than the weight of the ball. The net force is in the upward direction and the ball accelerates upward. When the ball's shape is the shape it has when it is sitting still on the floor, (just slightly squashed), the net force is zero. When its shape relaxes further, the net force is in the downward direction. But it already has velocity in the upward direction, so it keeps on going upward until its speed has decreased to zero. Because some of its initial gravitational potential energy has been converted into thermal energy it does not regain its initial height.
A particular ball is characterized by its coefficient of restitution, the ratio of its rebound speed to its collision speed just above the surface of the perfectly hard floor. A perfectly hard floor is a floor that does not move itself.
coefficient of restitution = (outgoing speed)/(incoming speed)
The coefficient of restitution depends on the material the ball is made of and is always smaller than 1. The coefficient of restitution is a ratio of speeds. To find the ration of the outgoing to the incoming kinetic energy we use
Kout/Kin = v2out/v2in = (coefficient of restitution)2.
Real surfaces are not perfectly hard. They distort when hit by the ball. They store energy themselves, and return some of it to the ball as it rebounds. "Lively" surfaces, such as a trampoline, store energy very efficiently and return almost all of it to the rebounding object.
An elastic ball that wastes 30% of the collision energy as heat when it bounces on a hard floor. To what fraction of its original height will it rebound? What is its coefficient of restitution?
Solution: