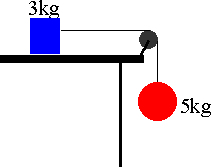
 The coefficient of friction between the 3 kg mass and the surface in the
figure below is 0.4. The system starts from rest. What is the
speed of the 5 kg mass when it has fallen 1.5 m?
The coefficient of friction between the 3 kg mass and the surface in the
figure below is 0.4. The system starts from rest. What is the
speed of the 5 kg mass when it has fallen 1.5 m?
If a system of objects is isolated from its environment and does
not interact with its environment at all, then certain physical quantities of
the system cannot change. They are constant or conserved.
Conservation laws are considered to be the most fundamental principles of
physics.
Energy is
conserved for an isolated system. There are, however, no truly isolated
systems. Interactions with the environment can be only approximately excluded. So
while conservation laws are very useful in analyzing many everyday situations,
they strictly hold only for the universe as a whole.
Energy conservation
for an isolated system is a fundamental principle of physics. Energy for
an isolated system is always conserved. It may change forms, but the total
amount of energy in an isolated system is constant. Energy can, however,
be converted from one form to another form. Work is the conversion of one
form of energy into another. Energy comes in different forms, kinetic
energy, potential energy, chemical energy, thermal energy, etc. If an
object has energy, it has the potential to do work.
There are several forms of potential energy. Kinetic and potential energy
are called mechanical energy or
ordered energy.
Thermal energy is disordered energy. Friction converts mechanical
energy into disordered energy.
When no disordered energy is produced, then mechanical energy is conserved. Conservative forces conserve mechanical energy and do not produce disordered energy.
Kinetic energy is the energy of moving
objects.
Examples are:
Potential Energy is stored energy which
can be converted into kinetic energy.
Examples are:
Formulas for forms of energy we are already familiar with:
When a system is acted on by an external force, then energy can be transferred into or out of the system. An external force can do work against internal forces and change the potential energy of the system or it can be a net force changing the kinetic energy of the system. The work Wext done by the external force on a conservative system may be written as Wext = ∆K + ∆U.
The external force can be conservative or non-conservative. The work done by or against a conservative force converts one form ordered energy into another form of ordered energy. Forces that do work converting ordered energy into disordered energy are non-conservative forces.
From a 50 m high platform a 0.1 kg stone is thrown straight upward with initial speed 5 m/s. What is it speed 10 m above the ground?
Solution:
A 70 kg diver steps off a 10 m tower and drops straight down into the water. If he comes to rest 5 m below the surface of the water, determine the average resistance force exerted on the diver by the water.
Solution:
A 6*105 kg subway train is brought to a stop from a speed of 0.5 m/s in 0.4 m by a large spring bumper at the end of its track. What is the force constant k of the spring?
Solution:
Microscopically all known forces are conservative. Therefore, microscopically, all energy is either kinetic or potential energy.
"There is a fact, or if you wish, a law, governing all natural
phenomena that are known to date. There is no known exception to this law--it is
exact so far as we know. The law is called the conservation of energy. It states that there is a certain quantity,
which we call energy, that does not change in the manifold of changes which
nature undergoes. That is a most abstract idea,
because it is a mathematical principle; it says that there is a
numerical quantity which does not change when something happens. It is not a
description of a mechanism, or anything concrete; it is just a strange fact that
we can calculate some number, and when we finish watching nature go through her
tricks and calculate the number again, it is the same."
Richard Feynman
Macroscopically, ordered energy can easily and completely be converted into other forms. Gravitational potential energy is an example of ordered energy. The gravitational potential energy stored in a car on top of a hill is converted into kinetic energy and thermal energy as it rolls towards the bottom of the hill. Hydroelectric plants convert the gravitational potential energy stored in the water in a reservoir into electric energy. Kinetic energy also can be easily converted. Kinetic energy is the energy an object has because it is moving.
Thermal energy cannot easily and completely converted into other forms. Thermal energy is disordered energy. The individual atoms and molecules that make up an object have potential and kinetic energy, but they move in a random fashion about their equilibrium positions in the object, so that the object as a whole remains at rest. The more kinetic energy is stored in the random motion of the atoms or molecules, the higher is the temperature of the object.
 The coefficient of friction between the 3 kg mass and the surface in the
figure below is 0.4. The system starts from rest. What is the
speed of the 5 kg mass when it has fallen 1.5 m?
The coefficient of friction between the 3 kg mass and the surface in the
figure below is 0.4. The system starts from rest. What is the
speed of the 5 kg mass when it has fallen 1.5 m?
Solution:
What is the difference between "energy conservation "in everyday language and the law of conservation of energy? Give some examples of each.
Discuss this with your fellow students in the discussion forum!