Assume that you need to calculate the rate of heat flow through a window.  The flow depends on many factors.  The window area is one of them.  How do you find this area?

For a rectangular widow, you just multiply the widths of the window by the height of the window.
Let us write this in a slightly awkward form.
Let the x-axis be the horizontal axis and the y-axis the vertical axis.
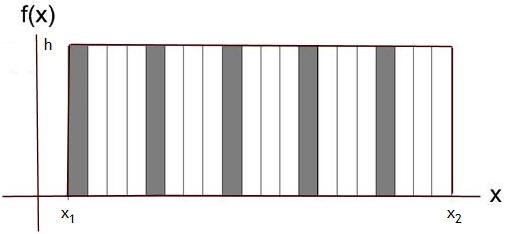
Let the left corner of the window be at x₁ and the right corner at x₂.
The width of the window is ∆x = x₂ - x₁.
Let the height of the window be y = f(x) = h.
The area of the window then is A = f(x)∆x = h(x₂ - x₁).

Now assume that the window is not rectangular, but has a parabolic shape.  The base of the window still extends from x₁ to x₂.   But for the height y we have

y = f(x) = (4h/∆x²)[-x² + (2x₁ + ∆x)x - x₁(x₁ + ∆x)].

This is the equation of a parabola which crosses the x-axis at x₁ and x₁ + ∆x and has a height h.

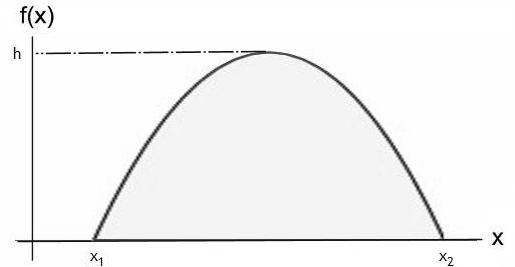
How do we find the area of this window? 
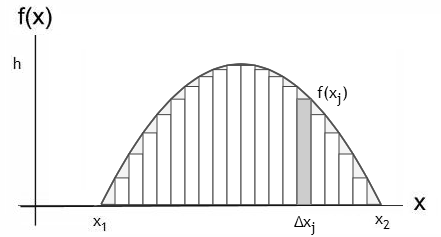
Let us find the approximate area by dividing the region between x₁ and x₂ into N equal intervals ∆x_i, i = 1 to N.
If N is large enough and therefore ∆x_i is small enough, the area of the window above the jth interval ∆x_j is very close to the area of the rectangle f(x_j)∆x_j.
We can then find the area of the widow by summing the areas of all the small rectangles.

A = ∑₁^N f(x_i)∆x_i.

The sum is over all i, from 1 to N.

We can do this, for example, using a spreadsheet.  The smaller we make ∆x_i, the closer our calculated area approaches the true area of the window.  Letting ∆x_i --> 0 ,we convert the sum to a definite integral.
The notation is lim_∆xi-->0 ∑_x1^x2f(x_i)∆x_i = ∫_x1^x2f(x)dx.  Here dx stands for the infinitesimally small interval.

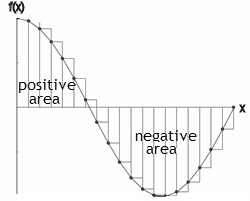
A definite integral represents the area under a curve f(x) from some starting position x_i to some ending position x_f.

Areas above the x-axis are positive, and areas below the x-axis are negative.

A spreadsheet (or other computer programs) can be used to evaluate a definite integral numerically by converting it into a sum over a large number of very small intervals.  Evaluating a definite integral analytically (if possible) is a quicker way of finding the area under a curve.

For many common function f(x) you can look up a formula ∫f(x)dx in a table of integrals or online.
For example if f(x) = c*xⁿ, with c a constant and n any number not equal to -1, then

∫f(x)dx = ∫c*xⁿdx = F(x) = c*xⁿ⁺¹/(n+1).

The definite integral ∫_x1^x2f(x)dx is the found by evaluating F(x) at the integration limits.
∫_x1^x2f(x)dx = F(x)|_x1^x2 = F(x₂) - F(x₁).
For example ∫_x1^x2 c*xⁿdx = c*x₂ⁿ⁺¹/(n+1) -  c*x₁ⁿ⁺¹/(n+1).

Finding the area of our window with

f(x) = (4h/∆x²)[-x² + (2x₁ + ∆x)x - x₁(x₁ + ∆x)],

we integrate f(x) from x₁ to x₂ = x₁ + ∆x.

∫f(x)dx = (4h/∆x²)[-∫x²dx + (2x₁ + ∆x)∫x¹dx - x₁(x₁ + ∆x) ∫x⁰dx]
 =-(4h/∆x²)[-x²/3 + (2x₁ + ∆x)x²/2 - x₁(x₁ + ∆x) x¹/1]  = F(x)
∫ _x1^x2f(x)dx = F(x₂) - F(x₁).

Note that you can factor out constants to simplify the notation.

Let us simplify and chose x₁ = 0, x₂ = 1 and h = 1.  The ∆x = 1.
Then f(x) = 4[-x² + x],  ∫f(x)dx = 4[-∫x²dx + ∫xdx] = 4[-x³/3 + x²/2] = F(x)
F(x₂) - F(x₁) = 4[-1/3 + 1/2]  = 2/3.
Compare this with the result of the numerical integration using the spreadsheet.

This semester we will only encounter a few integrals.
The once you may encounter are

• ∫xⁿdx = xⁿ⁺¹/(n+1)  n ≠ -1,
• ∫x^-1dx = ln(x),
• ∫e^-axdx = e^-ax/a,
• ∫sin(x)dx = -cos(x),
• ∫cos(x)dx = sin(x).

Resources:
Definite Integral Calculator
Wolfram online integral calculator