The gravitational potential energy Ug is defined as the negative of the work done by the
gravitational force, or the work done by an applied force canceling the
gravitational force, in displacing an object from a reference position. If the
gravitational force acting on an object is pointing in the -y direction with
constant magnitude mg, and the reference position is at y = 0, then Ug
= mgy.
The zero of the gravitational potential energy, i.e. the reference position,
is chosen arbitrarily. However a difference in gravitational potential energy
∆Ug = mg∆y = mg(yf - yi)
is uniquely defined.
The gravitational potential energy gained by an object being lifted is equal
to the work done on the object by an applied force, which exactly cancels
gravity. The applied force does positive work. When the object is being
lifted, the gravitational force does negative work. The gravitational potential
energy can be converted back into other forms by letting the gravitational force
do positive work. If we let the object fall towards the ground it will lose
potential energy and gain kinetic energy.
Problem:
A 100 N crate sits on the ground and is attached to one end of a rope.
A person on a balcony pulls up on the rope,
lifting the crate a distance of 3 m. What is the change in the
gravitational potential energy of the crate?
Solution:
- Reasoning:
Near the surface of Earth the change in the gravitational potential energy
id ∆Ug = mg∆y, with the y-axis pointing up.
- Details of the calculation:
∆Ug = mg∆y = 100 N* 3m = 300 J. (Note: 100 N is
the weight of the crate, i.e. the gravitational force mg acting on it.
The mass of the crate is m = 100 N/9.8 m/s2 = 10.1 kg.)
Problem:
A 100 N crate sits on the ground and is attached to one end of a rope.
A person on a balcony pulls up on the rope with a constant force of 110 N
lifting the crate a distance of 3 m.
What is the kinetic energy of the crate when it reaches the height of 3 m?
Solution:
- Reasoning:
The net force on the crate is the difference between upward force from the
rope and the downward force of gravity.
Fnet*d = Wnet = ∆K. (work - kinetic energy
theorem)
- Details of the calculation:
Fnet = 110 N - 100 N = 10 N. Wnet = 10N *
3 m = 30 J = ∆K.
Since the crate starts with zero kinetic energy, its final kinetic energy is
30 J.
The applied force does 110 N * 3 m = 330 J of work. 300 N is converted
into potential energy and 30 N into kinetic energy.
Conservative Forces
The gravitational potential energy does not depend on the path.
Example:
 We do the same work lifting the motorcycle straight up onto the bed of the truck or
rolling it up a ramp.
We do the same work lifting the motorcycle straight up onto the bed of the truck or
rolling it up a ramp.
The gravitational force near the surface of the earth points vertically downward.
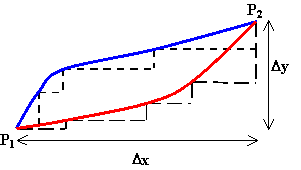
We can approximate any path between two points P1 and P2 by arbitrarily
small vertical and horizontal segments. The total horizontal and the total vertical displacement are the same for each path.
The gravitational force does no work along the horizontal segments of the path, since here
it is perpendicular to displacement vector. It does work Wi = -mg∆yi along each vertical segment of length
∆yi.
The total work done by the gravitational force is W = -mg∆ytotal
= -mgh. The change in potential energy is Ug = mgh.
A potential energy function is a function of the
position of an object. It can be
defined only for conservative forces.
A force is conservative if the work it does on an object depends only on the
initial and final position of the object and not on the path. The gravitational force is a
conservative force. The potential energy function associated with the
gravitational force near the surface of the earth is Ug = mgy if the reference point is chosen at
y = 0. (Ug only depends on the position of an object, not on how the
object reached that position.)
Another example of a conservative force is the force exerted by a spring.
The elastic potential energy function is Us
= ½kx2, where x is the displacement from equilibrium.
Us only depends on how much the spring is stretched or compressed,
not on how this was accomplished.
Problem:
A 100 N force is used to stretch a spring with spring constant k = 2000 N/m.
(a) What is the maximum stretch this force can produce?
(b) How much elastic potential energy is stored in the spring at the
maximum stretch?
Solution:
- Reasoning:
The spring obeys Hooke's law. At maximum stretch Fext
= kx.
The elastic potential energy stored in the spring is Us
= ½kx2.
- Details of the calculation:
(a) x = Fext/k = (100 N)/(2000 N/m) = 0.05 m = 5 cm.
(b) The elastic potential energy stored in the spring is
Us
= ½kx2 = ½(2000 N/m)(0.05 m)2 = 2.5 J.
When the a conservative force does work on an object, the potential energy of the object changes. We may write
Fx∆x = -∆U or Fx = -∆U/∆x.
Fx = -∆U/∆x (as ∆x --> 0) holds for any conservative force in one dimension.
If we know the potential energy function for the object, we can calculate the
conservative force acting on the object.
The conservative internal force acting between parts of the system equals the negative
derivative of the potential energy associated with that system.
Module 6: Question 1
Does the work you do on a book when you lift it onto a shelf depend on the
path taken? On the time taken? On the height of the shelf? On
the mass of the book?
Discuss this with your fellow students in the discussion forum!
Gravity
Locally, near the surface of the earth, the gravitational force is approximately
constant. In general, the gravitational force exerted by point object 1 on point object 2
is given by
F12 = (-G m1m2/r122)
(r12/r12).
Here r12 is the distance between particles 1 and 2, and (r12/r12)
is the unit vector pointing from particle 1 to particle 2.
G is the gravitational constant, G = 6.67*10-11 Nm2/kg2.
The above formula is also valid for spherical objects with r12 denoting the
distance between their centers. The formula is always approximately valid as long as the
distance between the objects is much larger than their respective sizes. When the distance between the objects changes, the gravitational force does work.
The
change in the gravitational potential energy is
Uf - Ui = -∫r12ir12f
F12·dr12 = -G m1m2∫r12ir12f
(1/r122) dr12 = -G m1m2(1/r12f
- 1/r12i).
The difference in the gravitational potential energy is uniquely defined.
To agree on
the value of the gravitational potential energy we need to agree on a reference point r12i.
Often this reference point is chosen to be at infinity. Then
Ug(r12) = -Gm1m2/r12.
The gravitational potential energy of two objects (stars, planets, satellites)
separated by a distance d then is negative, Ug = -Gm1m2/d.
Its absolute value is equal to the amount of work that needs to be done to completely
separate the objects, i.e. to let d go to infinity.
Problem:
How much energy is required to move a 1000 kg mass from the Earth's surface
to an altitude twice the Earth's radius?
Solution:
- Reasoning:
We assume the object does not gain any kinetic energy.
Uf - Ui = -∫r12ir12f
F12·dr12 = -(work done by
gravitational force) = (work done by external force)
- Details of the calculation:
W = Uf - Ui = -G m1m2(1/r12f
- 1/r12i).
G = 6.67*10-11 Nm2/kg2.
m1 = mearth = 5.98*1024 kg.
m2 = 1000 kg.
r12i = 6.37*106m.
r12f = 2r12i.
W = 3.13*1010 J.
 We do the same work lifting the motorcycle straight up onto the bed of the truck or
rolling it up a ramp.
We do the same work lifting the motorcycle straight up onto the bed of the truck or
rolling it up a ramp.