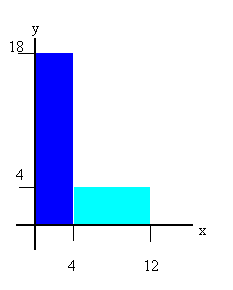The center of gravity of an object is the
point from which you can suspend an object at rest, and, no matter how the
object is oriented, gravity will not cause it to start rotating. If you suspend
an object from any point and let it come to rest, the center of gravity will lie
somewhere on a vertical line that passes through the point of suspension. Near
the surface of the earth, where the gravitational acceleration is (nearly)
constant, the center of gravity coincides with the center of mass.
Assume a system consist of a collection of particles, for example the atoms
that make up a solid object. The mass of the ith particle is mi
and its position coordinates are (xi, yi, zi).
The coordinates of the center of mass (CM) are given by
xCM =
Σmixi/M, yCM = Σmiyi/M,
zCM = Σmizi/M.
Here M is the total mass of the system.
M = Σmi.
The ∑ symbol stand for sum. The sum is over all the particles that make up the system.
The position vector of the center of mass is rCM.
rCM = xCM
i + yCM j + zCM
k = (Σmixi i + Σmiyi
j + Σmizi k)/M
rCM = (Σmiri)/M.
Why do we care about this special point called the center of mass?
Let us find its velocity and its acceleration.
vCM = drCM/dt = (Σmi dri/dt)/M
= (Σmivi)/M.
MvCM = Σmivi = Σpi
= ptot.
The velocity of the center of mass multiplied by the
total mass of the system is equal to the total momentum of the system.
aCM = dvCM/dt = (Σmi dvi/dt)/M
= (Σmivi)/M.
MaCM = Σmiai = ΣFi
= Ftot.
The acceleration of the center of mass multiplied by
the total mass of the system is equal to the total force acting on the system.
Newton's 2nd law, F = ma, when applied to an
extended object, predicts the motion of a particular reference point for this
object. This reference point is called the center of
mass. The center of mass of a system moves as if the
total mass of the system were concentrated at this special point. It responds
to external forces as if the total mass of the system were concentrated at this point.
The total force on a particle, Fi, is the
vector
sum of all internal and external forces acting on the particle. If we
sum the forces acting on all the particles of the system, then in this vector
sum every internal force that particle 1 exerts on particle 2 is cancelled by
the internal force that particle 2 exerts on particle 1. This is a consequence
of Newton's third law.
We therefore have Ftot = ∑Fi = ∑Fext.
The total force on the system is the vector sum of all the external forces.
But Ftot = MaCM = dpCM/dt.
The total momentum of the system only changes, if
external forces are acting on the system. The center of mass of the system only
accelerates, if external forces are acting on the system.
If only internal forces are acting on the particles that make up the system,
then the center of mass does not accelerate, its velocity remains constant. The
total linear momentum of the system is conserved.
For the total linear momentum of a system to be constant, the particles
making up the system can move with respect to each other, and can accelerate
with respect to each other, but they must move and accelerate in such a way that
vCM = constant and therefore aCM = 0.
How do we find the center of mass (CM) of of an object?

 Every extended object has a center of mass.
If near the surface of Earth an object, in any
orientation, is supported at a location directly below its center of mass or
suspended from a location directly above its center of mass, it will be balanced
and it will not start to rotate.
Every extended object has a center of mass.
If near the surface of Earth an object, in any
orientation, is supported at a location directly below its center of mass or
suspended from a location directly above its center of mass, it will be balanced
and it will not start to rotate.
Usually, but not always, the center of mass
of an object lies within the object
itself. For example, the center of mass of a ball is the very middle of
the ball, and the center of mass of a book is the middle of the book.
 If an object has parts that can move with respect to each
other, the location of the center of mass depends on the positions
of the parts. For example, when a
cheerleader lifts her arms,
her center of mass moves to
a higher position in her body than
when her arms are at her side.
If an object has parts that can move with respect to each
other, the location of the center of mass depends on the positions
of the parts. For example, when a
cheerleader lifts her arms,
her center of mass moves to
a higher position in her body than
when her arms are at her side.
Where is the center of mass (CM) of a person?
In most men, the center of mass is
located at or slightly above the navel, in most women it is located
below the navel, closer to the hips.
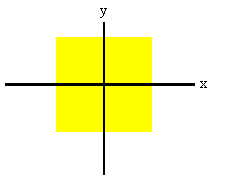 For a homogeneous, symmetrical system, the center of mass always lies on the
symmetry axis.
For a homogeneous, symmetrical system, the center of mass always lies on the
symmetry axis.
Consider a square with sides of length a. We can position our coordinate
system as shown.
The x and y axes are symmetry axes. We can easily verify that xCM
= 0, yCM = 0 from symmetry.
The center of mass lies on the
intersection of the symmetry axes, at the origin.
Problem:
Four objects are situated along the y-axis as follows: a 2 kg object is at +3 m, a 3 kg object is at +2.5 m, a 2.5 kg object is at the origin, and a 4 kg object
is at -0.5 m. Where is the center of mass of these
objects?
Solution:
- Reasoning:
The coordinates of the center of mass (CM) of a system of objects are
xCM =
Σmixi/M, yCM = Σmiyi/M,
zCM = Σmizi/M.
Here M is the total mass of the system, M = Σmi.
- Details of the calculation:
The total mass of the system is M = (2 + 3 + 2.5 + 4) kg = 11.5 kg.
yCM
= (2 kg *
3 m + 3 kg * 2.5 m + 2.5 kg * 0 m - 4 kg
* 0.5 m)/(11.5 kg) = 1 m.
xCM = zCM = 0.
Problem:
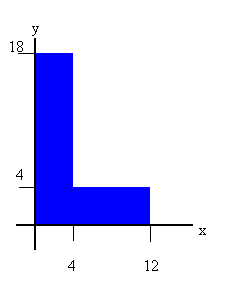 A uniform carpenter's square has the shape of an L, as shown in the figure.
Locate the center of mass relative to the origin of the coordinate
system.
A uniform carpenter's square has the shape of an L, as shown in the figure.
Locate the center of mass relative to the origin of the coordinate
system.
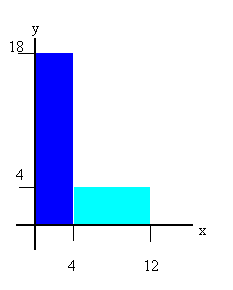
Solution:
- Reasoning:
We can think of the system as being made up of two subsystems, as shown
in the figure.
The CM of the left subsystem lies at xCM = 2 cm, yCM
= 9 cm. The CM of the
right subsystem lies at xCM = 8 cm, yCM
= 2 cm. If the mass of a 1 cm by 1 cm square is 1 unit, then the mass
of the left subsystem is 72 units and the mass of the right subsystem is 32
units. We find the CM of the system by treating each subsystem as a
separate particle, with all its mass concentrated at its center of mass.
Then we have for the whole system
- Details of the calculation:
xCM = (72 units *
2 cm + 32 units * 8 cm)/(104 units)
= 3.85 cm,
yCM = (72 units *
9 cm + 32 units * 2 cm)/(104 units) = 6.85 cm.
The CM of the system lies outside of the system. For irregular-shaped
objects it is quite common for the CM to lie outside the system. This
special point outside the system responds to external forces as if the total
mass of the system were concentrated there.
Problem:
The mass of the Moon is 7.35*1022 kg and the mass of the Earth is
6.00*1024 kg. The distance between the Moon and the Earth is 3.80*105
km.
Choose your coordinate system so that the center of the Earth is at the origin
and the center of the Moon is on the x-axis at x = 3.80*108 m.
Calculate the location xcm of the center of mass of the Earth-Moon
system
Solution:
- Reasoning:
The x-coordinate of the center of mass (CM) of a system of objects is
xCM =
Σmixi/M.
- Details of the calculation:
xcm = (0 m*6.00*1024 kg + 3.80*108 m*7.35*1022
kg)/(6.00*1024 kg + 7.35*1022 kg)
= 4598666 m = 4600 km.
Since the radius of the Earth is 6378 km, the center of mass of the
Earth-Moon system is inside the Earth.
Problem:
A baseball bat with uniform density is cut at the location of its center of
mass as shown in the figure.

After the cut, which piece has the smaller mass?
Solution:
- Reason it out yourself and then watch this
video clip. Was your answer correct?
 Every extended object has a center of mass.
If near the surface of Earth an object, in any
orientation, is supported at a location directly below its center of mass or
suspended from a location directly above its center of mass, it will be balanced
and it will not start to rotate.
Every extended object has a center of mass.
If near the surface of Earth an object, in any
orientation, is supported at a location directly below its center of mass or
suspended from a location directly above its center of mass, it will be balanced
and it will not start to rotate.
 If an object has parts that can move with respect to each
other, the location of the center of mass depends on the positions
of the parts. For example, when a
cheerleader lifts her arms,
her center of mass moves to
a higher position in her body than
when her arms are at her side.
If an object has parts that can move with respect to each
other, the location of the center of mass depends on the positions
of the parts. For example, when a
cheerleader lifts her arms,
her center of mass moves to
a higher position in her body than
when her arms are at her side. For a homogeneous, symmetrical system, the center of mass always lies on the
symmetry axis.
For a homogeneous, symmetrical system, the center of mass always lies on the
symmetry axis.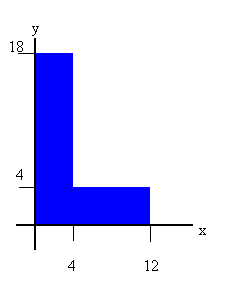 A uniform carpenter's square has the shape of an L, as shown in the figure.
Locate the center of mass relative to the origin of the coordinate
system.
A uniform carpenter's square has the shape of an L, as shown in the figure.
Locate the center of mass relative to the origin of the coordinate
system.