Consider two interacting objects.  If object 1 pushes on object 2 with a force F = 10 N for 2 s to the right, then the momentum of object 2 changes by 20 Ns = 20 kgm/s to the right.  By Newton's third law object 2 pushes on object 1 with a force F = 10 N for 2 s to the left.  The momentum of object 1 changes by 20 Ns = 20 kgm/s to the left.  The total momentum of both objects does not change.  For this reason we say that the total momentum of the interacting objects is conserved. 

Newton's third law implies that the total momentum of a system of interacting objects not acted on by outside forces is conserved.

The total momentum in the universe is conserved.  The momentum of a single object, however, changes when a net force acts on the object for a finite time interval.  Conversely, if no net force acts on an object, its momentum is constant.

For a system of objects, a component of the momentum along a chosen direction is constant, if no net outside force with a component in this chosen direction acts on the system.

Problem:

A 0.1 kg ball is thrown straight up into the air with an initial speed of 15 m/s.  Find the momentum of the ball
(a)  at its maximum height and
(b)  half way up to its maximum height.

Solution:

• Reasoning:
  p = mv.  F = dp/dt = mdv/dt.
  The gravitational force is a conservative force.
• Details of the calculation:
  (a) At the ball's maximum height its velocity is zero, and therefore its momentum is zero.

  (b) The ball's total energy E = K + U is constant.  
  Initially U = 0 and K = (1/2)mv² =(0.05 kg)(15 m/s)² = 11.25 J.  
  At its maximum height K = 0 and U = mgh = 11.25 J.
  Halfway up to its maximum height K = U = (1/2)11.25 J.  
  Therefore v² = 2K/m = (11.25 J)/(0.1 kg) = 112.5 (m/s)², 
  v = 10.6 m/s, p =( 0.1 kg)(10.6 m/s) = 1.06 kgm/s.
  The momentum of the ball changes, because a net force is acting on it.

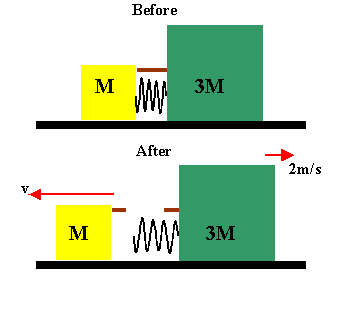
Problem:

Two blocks of mass M and 3 M are placed on a horizontal frictionless surface.  A light spring is attached to one of them, and the blocks are pushed together with the spring between them.  A cord holding them together is burned, after which the block of mass 3 M moves to the right with a speed of 2 m/s.
(a)  What is the speed of the block of mass M?
(b)  Find the original elastic potential energy in the spring if M = 0.35 kg.

Solution:

• Reasoning:
  The total initial momentum of the system is zero.  No outside force act on the system in the horizontal direction, so the final horizontal momentum component of the system is also zero.  The elastic spring force is conservative.  The total energy E = K + U of the system is conserved. 
• Details of the calculation:
  (a)  The final horizontal momentum component of the system is also zero.
  p_3M + p_M = 0.
  p_3M = (3 M)(2 m/s), p_M = -(3 M)(2 m/s) = -6 M m/s. 
  v_M = -6 m/s.  The block of mass M moves towards the left with a speed of 6 m/s.

  (b) The total energy E = K + U of the system is conserved. 
  After the string has been cut and the spring has relaxed,
  E = K = (1/2)(3 M)(2 m/s)² + (1/2)M(6 m/s)² = 8.4 J. 
  Initially E = U = 8.4 J, the total energy is the elastic energy stored in the spring.

Collisions

In collisions between two isolated objects Newton's third law implies that momentum is always conserved.  In collisions, it is assumed that the colliding objects interact for such a short time, that the impulse due to external forces is negligible.  Thus the total momentum of the system just before the collision is the same as the total momentum just after the collision. 
Collisions in which the kinetic energy is also conserved, i.e. in which the kinetic energy just after the collision equals the kinetic energy just before the collision, are called elastic collision.  In these collisions no ordered energy is converted into thermal energy. 
Collisions in which the kinetic energy is not conserved, i.e. in which some ordered energy is converted into internal energy, are called inelastic collisions.  If the two objects stick together after the collision and move with a common velocity v_f, then the collision is said to be perfectly inelastic.

Note:
In collisions between two isolated objects momentum is always conserved.
Kinetic energy is only conserved in elastic collisions.

We always have m₁v_1i + m₂v_2i = m₁v_1f + m₂v_2f.
Only for elastic collisions do we also have ½m₁v_1i² + ½m₂v_2i² = ½m₁v_1f² + ½m₂v_2f².

Problem:

If two objects collide and one is initially at rest, is it possible for both to be at rest after the collision?  Is it possible for one to be at rest after the collision?  Explain!

Solution:

• Reasoning:
  In collisions between two objects momentum is conserved.  Since the initial momentum is not zero, the final momentum is not zero.  Both objects cannot be at rest.
  It is possible for one of the objects to be at rest after the collision.  For example, if the masses of the two objects are equal, then after a head-on elastic collision the object initially at rest is moving and the object initially moving is at rest.

Problem:

A 10 g bullet is stopped in a block of wood (m = 5 kg).  The speed of the bullet-wood combination immediately after the collision is 0.6 m/s.  What was the original speed of the bullet?

Solution:

• Reasoning:
  This is a perfectly inelastic collision.  The two objects stick together after the collision and move with a common velocity v_f.  Assume the motion is along the x-direction.  We then have
  m₁v₁ + m₂v₂ = (m₁ + m₂)v_f.
  m₁ is the mass of the bullet, v₁ its initial velocity, m₂ is the mass of the block, v₂ its initial velocity.
• Details of the calculation:
  Initially the block is at rest, v₂ = 0.  Therefore
  (0.01 kg)v₁ = (5.01 kg)(0.6 m/s).  v₁ = 300.6 m/s.

Problem:

Two cars of equal mass and equal speeds collide head on.  Do they experience a greater force if the collision is elastic or perfectly inelastic and they stick together?

Solution:

• Reasoning:
  Let the cars move along the z-axis.  When the collision is elastic, the change in momentum of the car moving initially in the positive x-direction is p_final - p_initial = -2 p_initial, since the car bounces back and  p_final = -p_initial.  When the collision is inelastic, the cars come to rest and the change in momentum of the car moving initially in the positive x-direction is p_final - p_initial = p_initial, since p_final = 0.  So the impulse has twice the magnitude in the elastic collision.  If the collisions last about the same amount of time, then the average force experienced by the car is twice as large in the elastic collision.

Problem:

A 90 kg fullback running east with a speed of 5 m/s is tackled by a 95 kg opponent running north with a speed of 3 m/s.  If the collision is perfectly inelastic, calculate the speed and the direction of the players just after the tackle.

Solution:

• Reasoning:
  Momentum is a vector.  In the collision, the total momentum is conserved.
• Details of the calculation:
  The initial momentum of player 1 is p₁ = (90 kg)(5 m/)s i = 450 kgm/s i.
  The initial momentum of player 2 is p₂ = (95 kg)(3m/s) j = 285 kgm/s j.
  Momentum is conserved, the final momentum p of both players is p = p₁ + p₂.
  p = (m₁ + m₂)v.
  v = 2.432 m/s i + 1.54 m/s j.
  v² = 8.29 (m/s)², v = 2.88 m/s.
  The speed of the players after the collision is 2.88 m/s.
  tanθ = p_y/p_x = 285/450 = 0.63, θ = 32.34^o.
  Their direction of travel makes an angle θ = 32.34^o with the x-axis.  (The x-axis is pointing east.)

Problem:

A 30,000 kg freight car is coasting at 0.850 m/s with negligible friction under a hopper that dumps 110,000 kg of scrap metal into it.  What is the final velocity of the loaded freight car?

Solution:

• Reasoning:
  For a system of objects, a component of the momentum along a chosen direction is constant, if no net outside force with a component in this chosen direction acts on the system.
• Details of the calculation:
  Let the direction of motion of the car be the positive x-direction.
  Before the dump the momentum of the car was in the x-direction with magnitude p = mv = 2.55*10⁴ kgm/s.
  The x- component of the momentum of the scrap metal was zero,
  so the total initial momentum in the x-direction was p_i = 2.55*10⁴ kgm/s.
  No external force acts on the objects in the x-direction, therefore the x-component of the total momentum is conserved.
  p_f = (m_car + m_metal)v_f = (140,000 kg)v_f = p_i = 2.55*10⁴ kgm/s.
  v_f = (2.55*10⁴ kgm/s)/(140,000 kg)= 0.182 m/s.

Problem:

A neutron in a reactor makes an elastic head-on collision with the nucleus of a carbon atom initially at rest.
(a) What fraction of the neutron's kinetic energy is transferred to the carbon nucleus?
(b) If the initial kinetic energy of the neutron is 1.6*10^-13 J, find its final kinetic energy and the kinetic energy of the carbon nucleus after the collision.
(The mass of the carbon nucleus is about 12 times the mass of the neutron.)

Solution:

• Reasoning:
  Energy and momentum are conserved in an elastic collision.
• Details of the calculation:
  (a) Initially the carbon nucleus is at rest.   Let particle 1 be the neutron and particle 2 be the carbon nucleus.   Assume the motion is along the x-direction.  We have

  (i) m₁v_1i  = m₁v_1f + m₂v_2f. (momentum conservation)
  (ii) (1/2)m₁v_1i²  = (1/2)m₁v_1f² + (1/2)m₂v_2f².  (energy conservation)
  We can solve this system of two equations for the ratio v_2f/v_1i. We obtain
  v_2f² = (m₁/m₂)(v_1i² - v_1f²)   from (ii),
  v_1f = v_1i - (m₂/m₁)v_2f    from (i).
  We can therefore write
  v_1f² = v_1i² + (m₂/m₁)²v_2f² - 2(m₂/m₁)v_1iv_2f.
  v_2f² = (m₁/m₂)(2(m₂/m₁)v_1iv_2f  - (m₂/m₁)²v_2f²) = (2v_1iv_2f  - (m₂/m₁)v_2f²).
  (1 + (m₂/m₁))v_2f = 2v_1i.
  v_2f = 2m₁v_1i/(m₁ + m₂).
  v_2f/v_1i = 2m₁/(m₁ + m₂) = 2/13 = 0.15
  The fraction of the kinetic energy transferred to the carbon nucleus is
  (m₂/m₁)(v_2f/v_1i)² = 12(0.15)² = 0.284.

  (b) The initial kinetic energy of the of the neutron is 160 fJ and the final kinetic energy of the carbon nucleus is 45.4 fJ.
  (1 femtoJoule = 1 fJ = 10^-15 J.)  The final kinetic energy of the neutron is (160 - 45.4) fJ.

Problem:

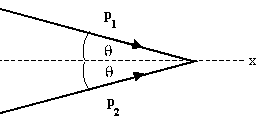
After a completely inelastic collision between two objects of equal mass, each having initial speed v, the two move off together with speed v/3.  What was the angle between their initial directions?

Solution:

• Reasoning:
  The external force acting on the system is zero, the total momentum is conserved.
  Assume that the final velocity of the objects points in the +x-direction.  Before the collision the velocity vector of both objects makes an angle θ with the x-axis as shown.
  
• Details of the calculation:
  p_1x + p_2x = p_fx = p_f,  p_1y + p_2y = 0.
  2mv cosθ = 2mv/3, cosθ = 1/3, θ = 70.5^o.
  The angle between their initial directions is 2θ = 141^o.

Problem:

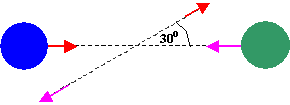
The mass of the blue puck is 20% greater than the mass of the green one.  Before colliding, the pucks approach each other with equal and opposite momenta, and the green puck has an initial speed of 10 m/s.  Find the speed of the pucks after the collision, if half the kinetic energy is lost during the collision.

Solution:

• Reasoning:
  The collision is inelastic, since energy is not conserved.
  The total momentum of the two pucks is zero before the collision and after the collision.
  Let particle 1 be the green puck and particle 2 be the blue puck.  Before and after the collision the ratio of the speeds is v₂/v₁ = m₁/m₂ = 1/1.2.
  The final kinetic energy of the system equals ½ times its initial kinetic energy.
  ½m₁v_1i² + ½m₂v_2i² = 2*(½m₁v_1f² + ½m₂v_2f²).
• Details of the calculation:
  ½m₁v_1i² + ½m₂v_2i² = 2*(½m₁v_1f² + ½m₂v_2f²).
  Algebra:
  m₁v_1i² + m₂v_2i² = 2 (m₁v_1f² + m₂v_2f²).
  m₁v_1i² + 1.2 m₁(v_1i/1.2)² = 2 (m₁v_1f² + 1.2 m₁(v_1f/1.2)²).
  m₁(v_1i² + v_1i²/1.2) = 2 m₁(v_1f² + v_1f²/1.2).
  v_1i² = 2 v_1f², v_1f = 0.707 v_1i.
  v_1f = 7.07 m/s,  v_2f = 5.89 m/s.

Module 7: Question 1

During a visit to the International Space Station, an astronaut was positioned motionless in the center of the station, out of reach of any solid object on which he could exert a force.  Suggest a method by which he could move himself away from this position, and explain the physics involved.

Discuss this with your fellow students in the discussion forum!

Module 7: Question 2

Football coaches advise players to block, hit, and tackle with their feet on the ground rather than by leaping through the air.  Using the concepts of momentum, work, and energy, explain how a football player can be more effective with his feet on the ground.

Discuss this with your fellow students in the discussion forum!

Links:

• Animations:  Momentum and Collisions
• The physics classroom:  Momentum and its conservation