Assume your file cabinet is sitting on a cart with wheels.  It is sitting in the middle of a room with a smooth floor.  You want to move it against the wall.  You give it a push.  It takes off, and before you know it, it slams into the wall.  It is hard to stop it, because it has linear momentum.

Linear momentum is a measure of an object's translational (as opposed to rotational) motion.  The linear momentum p of an object is defined as the product of the object's mass m times its velocity v.

p = mv.

Linear momentum is a vector.  Its direction is the direction of the velocity. 
The Cartesian components of p are p_x = mv_x,  p_y = mv_y,  p_z = mv_z.

If an object's velocity is changing, its linear momentum is changing.  For an object with constant mass we have

lim_∆t-->0 ∆p/∆t = m lim_∆t-->0 ∆v/∆t = m dv/dt = ma = F.

To change the linear momentum of an object of m, a net force has to act on it, causing the object to accelerate.  F = dp/dt is a different way of stating Newton's second law.  The rate at which an object's momentum changes is equal to the force acting on the object.  If a force F acts on an object for a time ∆t, then the change in the object's momentum is ∆p = F_avg∆t = ∫_ti^tf Fdt.  If ∆t is a very short time interval, we say that the object receives an impulse I = ∆p = F_avg∆t.

Note the difference:

Work: W = F_avg·d  (scalar)
Impulse: I = ∆p = F_avg∆t  (vector)

Problem:

What is the magnitude of the momentum of a fly if it is traveling with speed 1 m/s and has a mass of 0.0001 kg?

Solution:

• Reasoning:
  The magnitude of the momentum of an object is p = mv.
• Details of the calculation:
  The momentum of the fly is (0.0001 kg)(1 m/s) = 0.0001 kgm/s.

Problem:

A bullet is accelerated down the barrel of a gun by hot gases produced in the combustion of gun powder.  What is the average force exerted on a 0.03 kg bullet to accelerate it to a speed of 600 m/s in a time of 2.00 ms (milliseconds)?

Solution:

• Reasoning:
  The average force exerted is F_avg = ∆p/∆t.
  For vectors in one dimension, the sign is the direction indicator.
• Details of the calculation:
  Let the positive x direction point down the barrel.
  The change in momentum of the bullet is ∆p = p_f - p_i = (0.03 kg)*(600 m/s) = 18 kg m/s.
  The momentum changes in ∆t = 2*10^-3 s.
  F_avg = ∆p/∆t = (18 kg m/s)/(2*10^-3 s) = 9*10³ N.
  The force is positive, it points in the +x-direction.

Problem:

An object that has a small mass and an object that has a large mass have the same momentum p.  Which object has the largest kinetic energy?

Solution:

• Reasoning:
  The magnitude of each object's momentum is p. 
  The kinetic energy of an object is K = ½mv² = ½m²v²/m =  p²/(2m).
  The object with the larger mass has the smaller kinetic energy.

Problem:

An object that has a small mass and an object that has a large mass have the same kinetic energy.  Which mass has the largest magnitude of momentum p?

Solution:

• Reasoning:
  The kinetic energy of an object is K = ½mv².
  v² = 2K/m,  m²v² = p² = 2Km.  p = (2Km)^½.
  The object with the larger mass has the larger momentum p.

Problem:

A car is stopped for a traffic signal.  When the light turns green, the car accelerates, increasing its speed from 0 to 5.2 m/s in 0.832s.  What linear impulse and average force does a 70 kg passenger in the car experience?

Solution:

• Reasoning:
  Impulse: I = ∆p = m∆v.
• Details of the calculation:
  Assume the car accelerates in the x-direction.  The final momentum of the passenger is p_f = (70 kg)(5.2 m/s) = 364 kgm/s in the x-direction..  The initial momentum is zero. 
  ∆p = p_f - p_i = 364 kgm/s = F_avg∆t.  F_avg = (364 kgm/s)/(0.832 s) = 437.5 N in the x-direction.

Problem:

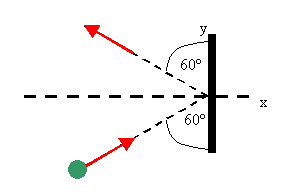A 3 kg steel ball strikes a wall with a speed of 10.0 m/s at an angle of 60^o with the surface.  It bounces off with the same speed and angle.  If the ball is in contact with the wall for 0.2 s, what is the average force exerted on the ball by the wall?

Solution:

• Reasoning:
  ∆p = p_f - p_i = F_avg ∆t.
  In this problem p_f and p_i do not point in the same direction.  We have to choose a coordinate system and find the components along the coordinate axes.
• Details of the calculation:
  Let i denote the positive x-direction and j the positive y-direction; i and j are unit vectors, they are direction indicators.
  The ball's initial momentum is
  p_i = p_xii + p_yij = (3 kg 10 m/s)sin60^o i + (3 kg 10 m/s)cos60^o j.
  Its final momentum is
  p_f = p_xfi + p_yfj = -(3 kg 10 m/s)sin60^o i + (3 kg 10 m/s)cos60^o j.
  ∆p = p_f - p_i = -2(30 kgm/s)sin60^o i = -(51.96 kgm/s) i.
  ∆p = F_avg ∆t. 
  F_avg = -(51.96 kgm/s) i/(0.2 s) = -259.8 i.

Problem:

Does a large force always produce a larger impulse on a body than a smaller force does?  Explain!

Solution:

• Reasoning:
  The impulse is the integral of force over time, I = ∆p = F_avg∆t.
  A small force acting over a long time can produce a larger impulse than a large force acting over a short time.