Balls hitting balls in different reference frames
 Assume two balls of equal mass, made from the same material, approach each other head
on. Both balls have the same speed v. They approach each other with
relative speed 2v.
As the balls collide, each ball exerts a force on the other. The forces are equal in magnitude but have opposite directions.
The balls distort like spherical springs, and the same amount of energy is stored in each ball
as elastic potential energy. It will be reconverted into kinetic energy.
The force with which ball 1 pushes on ball 2 first decelerates ball 2 to a stop and then accelerates it
into a direction opposite its initial velocity. The force with which ball 2 pushes on ball
1 decelerates ball one to a stop and then accelerates it into a direction opposite its
initial velocity. We expect the two balls to fly apart with equal speeds in opposite
directions. If the coefficient of restitution of the two balls is 1, then their speed will
not have changed. The total momentum of the two balls is conserved.
Assume two balls of equal mass, made from the same material, approach each other head
on. Both balls have the same speed v. They approach each other with
relative speed 2v.
As the balls collide, each ball exerts a force on the other. The forces are equal in magnitude but have opposite directions.
The balls distort like spherical springs, and the same amount of energy is stored in each ball
as elastic potential energy. It will be reconverted into kinetic energy.
The force with which ball 1 pushes on ball 2 first decelerates ball 2 to a stop and then accelerates it
into a direction opposite its initial velocity. The force with which ball 2 pushes on ball
1 decelerates ball one to a stop and then accelerates it into a direction opposite its
initial velocity. We expect the two balls to fly apart with equal speeds in opposite
directions. If the coefficient of restitution of the two balls is 1, then their speed will
not have changed. The total momentum of the two balls is conserved.
 Now suppose you are looking at this collision from a different reference
frame. Suppose as ball 1 approaches ball 2, you are sitting in a chair that
rolls with the same velocity right alongside ball 1. With respect to you, ball 1 does not
move. Ball 2 approaches ball 1 with speed 2v, the relative speed of the balls. After the
collision ball 2 has the same velocity as you do. So ball 2 now does not move with respect
to you, but ball 1 now moves backward with speed 2v. In your reference frame ball 2 hits a
stationary target. It comes to rest and ball 1 leaves the collision with a velocity equal
to the incoming velocity of ball 1. Momentum is conserved.
Now suppose you are looking at this collision from a different reference
frame. Suppose as ball 1 approaches ball 2, you are sitting in a chair that
rolls with the same velocity right alongside ball 1. With respect to you, ball 1 does not
move. Ball 2 approaches ball 1 with speed 2v, the relative speed of the balls. After the
collision ball 2 has the same velocity as you do. So ball 2 now does not move with respect
to you, but ball 1 now moves backward with speed 2v. In your reference frame ball 2 hits a
stationary target. It comes to rest and ball 1 leaves the collision with a velocity equal
to the incoming velocity of ball 1. Momentum is conserved.
Both reference frames are valid reference frames in which to describe the collision.
In any reference frame which is not accelerating, i.e. in any inertial frame, Newton's laws
are valid.
People in different reference frames see different things. They do not agree on the
velocity, momentum, or kinetic energy of objects. They will, however, always agree on the
relative velocity of two objects, and they will always be able to use Newton's laws in
their reference frame to explain what they are observing.
Bats and baseballs
 Assume a baseball hits a stationary bat. If the bat is nailed to the wall of
a house and cannot move at all, then the ball will just rebound the same way it
rebounds from a hard floor. If the bat is held in the hand of the batter, then
the force the ball exerts on the bat will accelerate the bat backwards, and some
collision energy will be transferred to the bat and will not appear as rebound
energy of the ball.
Assume a baseball hits a stationary bat. If the bat is nailed to the wall of
a house and cannot move at all, then the ball will just rebound the same way it
rebounds from a hard floor. If the bat is held in the hand of the batter, then
the force the ball exerts on the bat will accelerate the bat backwards, and some
collision energy will be transferred to the bat and will not appear as rebound
energy of the ball.
If the batter and the bat are very heavy, they receive little of the
collision energy, and the ball rebounds with outgoing speed equal to the
coefficient of restitution times the incoming speed.
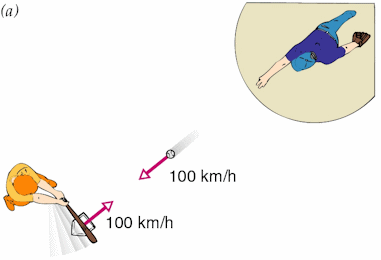
 If the batter is swinging the bat forward as the ball hits it, the ball's
outgoing speed will be much higher. Assume the bat and the ball each are moving
with speed 100 km/h in opposite direction. Their relative speed is 200 km/h. A
reference frame in which the bat is stationary is moving with 100 km/h speed
with the bat. In this reference frame the ball approaches with 200 km/h and
rebounds with speed v = coefficient of restitution times 200 km/h in the forward
direction. But this reference frame is moving itself with speed 100 km/h in the
forward direction. With respect to the ground the ball is therefore moving with
speed vground = 100km/h + v = 100km/h +
coefficient of restitution * 200 km/h.
If the batter is swinging the bat forward as the ball hits it, the ball's
outgoing speed will be much higher. Assume the bat and the ball each are moving
with speed 100 km/h in opposite direction. Their relative speed is 200 km/h. A
reference frame in which the bat is stationary is moving with 100 km/h speed
with the bat. In this reference frame the ball approaches with 200 km/h and
rebounds with speed v = coefficient of restitution times 200 km/h in the forward
direction. But this reference frame is moving itself with speed 100 km/h in the
forward direction. With respect to the ground the ball is therefore moving with
speed vground = 100km/h + v = 100km/h +
coefficient of restitution * 200 km/h.
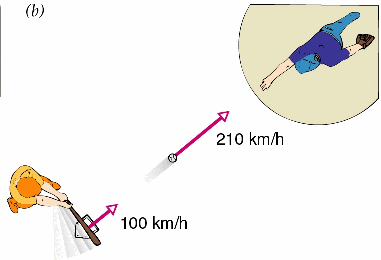
Example:
A baseball heads toward home plate at 100 km/h.
The bat heads toward the pitcher at 100 km/h.
The relative speed between ball and bat as they are approaching each
other is 200 km/h.
Assume the baseballs coefficient of restitution is 0.55. Just
after the collision the relative speed between ball and bat is
0.55*200 km/h = 110 km/h.
The bat still heads towards the pitcher at approximately 100 km/h.
The ball moves relative to the bat with a speed of 110 km/h
towards the pitcher.
Relative towards home plate and the pitcher, the ball's speed is
210 km/h. The ball heads toward pitcher at 210 km/h.
Animation: Ball hitting a stationary bat

Animation: Ball hitting a moving bat

 Assume two balls of equal mass, made from the same material, approach each other head
on. Both balls have the same speed v. They approach each other with
relative speed 2v.
As the balls collide, each ball exerts a force on the other. The forces are equal in magnitude but have opposite directions.
The balls distort like spherical springs, and the same amount of energy is stored in each ball
as elastic potential energy. It will be reconverted into kinetic energy.
The force with which ball 1 pushes on ball 2 first decelerates ball 2 to a stop and then accelerates it
into a direction opposite its initial velocity. The force with which ball 2 pushes on ball
1 decelerates ball one to a stop and then accelerates it into a direction opposite its
initial velocity. We expect the two balls to fly apart with equal speeds in opposite
directions. If the coefficient of restitution of the two balls is 1, then their speed will
not have changed. The total momentum of the two balls is conserved.
Assume two balls of equal mass, made from the same material, approach each other head
on. Both balls have the same speed v. They approach each other with
relative speed 2v.
As the balls collide, each ball exerts a force on the other. The forces are equal in magnitude but have opposite directions.
The balls distort like spherical springs, and the same amount of energy is stored in each ball
as elastic potential energy. It will be reconverted into kinetic energy.
The force with which ball 1 pushes on ball 2 first decelerates ball 2 to a stop and then accelerates it
into a direction opposite its initial velocity. The force with which ball 2 pushes on ball
1 decelerates ball one to a stop and then accelerates it into a direction opposite its
initial velocity. We expect the two balls to fly apart with equal speeds in opposite
directions. If the coefficient of restitution of the two balls is 1, then their speed will
not have changed. The total momentum of the two balls is conserved. Now suppose you are looking at this collision from a different reference
frame. Suppose as ball 1 approaches ball 2, you are sitting in a chair that
rolls with the same velocity right alongside ball 1. With respect to you, ball 1 does not
move. Ball 2 approaches ball 1 with speed 2v, the relative speed of the balls. After the
collision ball 2 has the same velocity as you do. So ball 2 now does not move with respect
to you, but ball 1 now moves backward with speed 2v. In your reference frame ball 2 hits a
stationary target. It comes to rest and ball 1 leaves the collision with a velocity equal
to the incoming velocity of ball 1. Momentum is conserved.
Now suppose you are looking at this collision from a different reference
frame. Suppose as ball 1 approaches ball 2, you are sitting in a chair that
rolls with the same velocity right alongside ball 1. With respect to you, ball 1 does not
move. Ball 2 approaches ball 1 with speed 2v, the relative speed of the balls. After the
collision ball 2 has the same velocity as you do. So ball 2 now does not move with respect
to you, but ball 1 now moves backward with speed 2v. In your reference frame ball 2 hits a
stationary target. It comes to rest and ball 1 leaves the collision with a velocity equal
to the incoming velocity of ball 1. Momentum is conserved. Assume a baseball hits a stationary bat. If the bat is nailed to the wall of
a house and cannot move at all, then the ball will just rebound the same way it
rebounds from a hard floor. If the bat is held in the hand of the batter, then
the force the ball exerts on the bat will accelerate the bat backwards, and some
collision energy will be transferred to the bat and will not appear as rebound
energy of the ball.
Assume a baseball hits a stationary bat. If the bat is nailed to the wall of
a house and cannot move at all, then the ball will just rebound the same way it
rebounds from a hard floor. If the bat is held in the hand of the batter, then
the force the ball exerts on the bat will accelerate the bat backwards, and some
collision energy will be transferred to the bat and will not appear as rebound
energy of the ball. If the batter is swinging the bat forward as the ball hits it, the ball's
outgoing speed will be much higher. Assume the bat and the ball each are moving
with speed 100 km/h in opposite direction. Their relative speed is 200 km/h. A
reference frame in which the bat is stationary is moving with 100 km/h speed
with the bat. In this reference frame the ball approaches with 200 km/h and
rebounds with speed v = coefficient of restitution times 200 km/h in the forward
direction. But this reference frame is moving itself with speed 100 km/h in the
forward direction. With respect to the ground the ball is therefore moving with
speed vground = 100km/h + v = 100km/h +
coefficient of restitution * 200 km/h.
If the batter is swinging the bat forward as the ball hits it, the ball's
outgoing speed will be much higher. Assume the bat and the ball each are moving
with speed 100 km/h in opposite direction. Their relative speed is 200 km/h. A
reference frame in which the bat is stationary is moving with 100 km/h speed
with the bat. In this reference frame the ball approaches with 200 km/h and
rebounds with speed v = coefficient of restitution times 200 km/h in the forward
direction. But this reference frame is moving itself with speed 100 km/h in the
forward direction. With respect to the ground the ball is therefore moving with
speed vground = 100km/h + v = 100km/h +
coefficient of restitution * 200 km/h.
