If we push on an object in the forward direction while the object is moving
forward, we do positive work on the object. The object accelerates,
because we are pushing on it. F = ma. The object gains kinetic energy.
The translational kinetic energy of an
object with mass m, whose center of mass is moving with speed v is K = ½mv2.
Translational kinetic energy = ½ mass * speed2
Kinetic energy increases quadratically with speed. When the speed of a car doubles,
its energy increases by a factor of four.
A rotating object has kinetic energy, even when the object as a whole has no
translational motion. If we consider the object made up of a collection of particles, then
each particle i has kinetic energy Ki = ½mivi2.
The total kinetic energy of the rotating object is therefore given by
K = ∑Ki = ∑½mivi2 = ∑½mri2ω2
= ½ω2 ∑mri2.
We write K = ½(∑mri2)ω2 = ½Iω2.
The quantity in parenthesis is called the moment of inertia I = ∑miri2
of the object
about the axis of rotation.
The moment of inertia of a system about an axis of
rotation can be found by multiplying the mass mi of each
particle in the system by the square of its perpendicular distance ri
from the axis of rotation, and summing up all these products,
I = ∑miri2.
For a system with a
continuous mass distribution the sum turns into an integral, I = ∫r2dm.
The units of the
moment of inertia are units of mass times distance squared, for example kgm2.
When an object is rotating about an
axis, its rotational kinetic energy is K = ½Iω2.
Rotational kinetic energy = ½ moment of inertia
* (angular speed)2.
When the angular velocity of a spinning wheel doubles, its kinetic energy increases by
a factor of four.
When an object has translational as well as rotational motion, we can look at
the motion of the center of mass and the motion about the center of mass
separately.
The total kinetic energy is the sum of the translational
kinetic energy of the center
of mass (CM) and the rotational kinetic energy about the CM.
The moment of inertia of an object depends on the
mass of the object, and on how this mass is distributed with respect to the axis of
rotation. The moment of inertia is
always defined with respect to an axis of rotation.
The farther the bulk of the mass is from the axis of rotation, the greater is
the rotational inertia (moment of inertia) of the object.
Example:
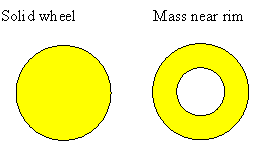 Imagine two wheels with the same mass. One is a solid wheel with its
mass evenly distributed throughout the structure, while the other has
most of the mass concentrated near the rim.
Imagine two wheels with the same mass. One is a solid wheel with its
mass evenly distributed throughout the structure, while the other has
most of the mass concentrated near the rim.
The wheel with the mass near the rim has the greater moment of
inertia.
Example:
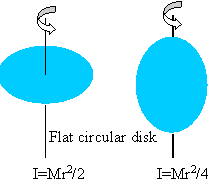 The moment of inertia of a circular disk spinning about an axis
through its center perpendicular to the plane of the disk differs from
the moment of inertia of a disk spinning about an axis through its
center in the plane of the disk.
The moment of inertia of a circular disk spinning about an axis
through its center perpendicular to the plane of the disk differs from
the moment of inertia of a disk spinning about an axis through its
center in the plane of the disk.
The moments of inertia of many objects with symmetric mass distribution of
about different symmetry axes can be looked up in tables.
Link: List
of moments of inertia
Problem:
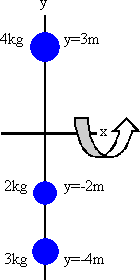 Three particles are connected by rigid rods of negligible mass lying along
the y-axis as shown.
Three particles are connected by rigid rods of negligible mass lying along
the y-axis as shown.
If the system rotates about the x-axis with angular speed of 2 rad/s,
find
(a) the moment of inertia about the x-axis and the total rotational
kinetic energy evaluated from ½Iω2,
and
(b) the linear speed of each particle and the total kinetic energy evaluated
from Σ½mivi2.
Solution:
- Reasoning:
The moment of inertia is I = ∑miri2.
Here ri is the perpendicular distance of particle i from
the x-axis.
The linear speed of particle i is vi
= ωri.
- Details of the calculation:
(a) I = (4 kg)(9 m2)
+
(2 kg)(4 m2) +
(3 kg)(16 m2) = 92 kgm2.
The rotational kinetic energy is K =
½Iω2
= 46*4/s2 = 184 J.
(b) The linear speed of the 4 kg mass is v = 6 m/s, and its kinetic energy is
½mv2
= 72 J.
The linear speed of the 2 kg mass is v = 4 m/s, and its kinetic energy is
½mv2
= 16 J.
The linear speed of the 3 kg mass is v = 8 m/s, and its kinetic energy is
½mv2
= 96 J.
The sum of the kinetic energies of the three particles is 184 J.
Problem:
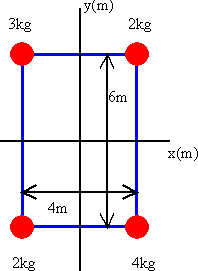 The four particles in the figure on the right are connected by rigid rods.
The origin is at the center of the rectangle. Calculate the moment of inertia of the system about the z-axis.
The four particles in the figure on the right are connected by rigid rods.
The origin is at the center of the rectangle. Calculate the moment of inertia of the system about the z-axis.
Solution:
- Reasoning:
The moment of inertia is I = ∑miri2.
Here ri is the perpendicular distance of particle i from
the z-axis.
- Details of the calculation:
Each particle is a distance
r = (9 + 4)½ m = (13)½ m from the
axis of rotation.
I = (3 kg + 2 kg + 4 kg + 2 kg)*13 m2 = 143 kgm2.
Problem:
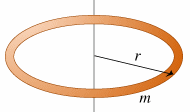 Find the moment of inertia of a very thin hoop of
mass m and radius r about its symmetry axis.
Find the moment of inertia of a very thin hoop of
mass m and radius r about its symmetry axis.
Solution:
- Reasoning:
The mass is continuously distributed, so the ∑m
--> ∫dm. All mass elements dm are a perpendicular
distance r from the axis of rotation.
I = ∫ r2dm = r2∫dm = mr2.
Parallel axis theorem
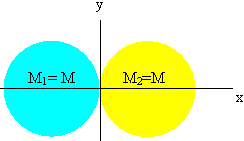 Consider a composite object, such as the two joined
disks in the figure on the right.
Consider a composite object, such as the two joined
disks in the figure on the right.
The center of mass of this object is at the origin. To find the moment of inertia of
the object about the CM we can use the parallel axis theorem.
This theorem states that the moment of inertia of an object about any axis is equal to the
sum of two terms. The first term is of the moment of inertia of the object about a
parallel axes through its center of mass. The second term is the product of the mass of
the object M times the square of the distance R of its center of mass from the axis in
question.
I = ICM + MR2.
We can treat the composite object as the sum of its parts, and for each part calculate
the moment of inertia about the z-axis.
For disk 1 we have I1 = ICM1 + M1R12,
and for disk 2 we have I2 = ICM22 + M2R22.
The moment of inertia of the composite object about the z-axis then is I = I1 + I2.
For a uniform disk of mass M the moment of inertia about an axis through its center and perpendicular to the plane of the disk is
½MR2.
For the object in the figure we therefore have for the moment of inertia about the
z-axis
I = (3/2)MR2 + (3/2)MR2 = 3MR2.
Rolling
The kinetic energy of an object with translational and rotational motion is
the sum of its translational and its rotational kinetic energy.
Translational kinetic energy = ½mvCM2.
Rotational kinetic energy = ½Iω2.
Total kinetic energy = ½mvCM2 + ½Iω2.
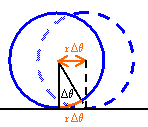 Consider a wheel of radius r and mass m rolling on a flat surface in the
x-direction.
Consider a wheel of radius r and mass m rolling on a flat surface in the
x-direction.
The displacement Δx and the angular displacement Δθ are related through
Δx = rΔθ.
The magnitudes of the linear velocity and the angular velocity are related through vCM = rω.
The kinetic energy of the wheel is the sum of the kinetic energy of the motion of the
center of mass ½mvCM2 = ½mr2ω2,
and the kinetic energy of the motion about the center of mass, ½Iω2.
Thee total kinetic energy is
KEtot = ½mr2ω2
+ ½Iω2 = ½[mr2 + I]ω2 = ½[m + I/r2]v2.
Example:
Assume the wheel is a uniform disk.
The moment of inertia I of a uniform disk about an axis perpendicular to the plane of the
disk through its CM is ½mr2.
The kinetic energy of the disk therefore is KEtot = (3/4)mr2ω2.
The ratio of the translational to the rotational kinetic energy is Etrans/Erot
= mr2/I.
If two rolling object have the same total kinetic energy, then the
object with the smaller moment of inertia has the larger
translational kinetic energy and the larger speed.
Problem:
Assume a disk and a ring with the same radius roll down an incline of height
h and angle theta. If they both start from rest at t = 0, which one will reach
the bottom first?


Solution:
- Reason it out yourself and then watch this
video clip. Was your answer correct?
Module 8: Question 2
Suppose you are designing a
race bicycle and it comes time to work on the wheels. You are told that the
wheels need to be of a certain mass but you may design them either as wheels
with spokes (like traditional bike wheels) or you may make them as having
solid rims all the way through. Which design would you pick given that the
racing aspect of the machine is the most important? Please explain!
Discuss this with your fellow students in the discussion forum!
Module 8: Question 3
Describe the energy transformations involved when a yo-yo is thrown downward
and then climbs back up its string to be caught in the user's hand.
Discuss this with your fellow students in the discussion forum!
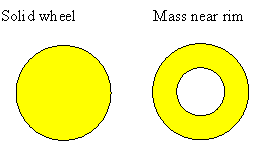 Imagine two wheels with the same mass. One is a solid wheel with its
mass evenly distributed throughout the structure, while the other has
most of the mass concentrated near the rim.
Imagine two wheels with the same mass. One is a solid wheel with its
mass evenly distributed throughout the structure, while the other has
most of the mass concentrated near the rim.
 The moment of inertia of a circular disk spinning about an axis
through its center perpendicular to the plane of the disk differs from
the moment of inertia of a disk spinning about an axis through its
center in the plane of the disk.
The moment of inertia of a circular disk spinning about an axis
through its center perpendicular to the plane of the disk differs from
the moment of inertia of a disk spinning about an axis through its
center in the plane of the disk.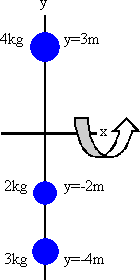 Three particles are connected by rigid rods of negligible mass lying along
the y-axis as shown.
Three particles are connected by rigid rods of negligible mass lying along
the y-axis as shown.
 The four particles in the figure on the right are connected by rigid rods.
The origin is at the center of the rectangle. Calculate the moment of inertia of the system about the z-axis.
The four particles in the figure on the right are connected by rigid rods.
The origin is at the center of the rectangle. Calculate the moment of inertia of the system about the z-axis.
 Find the moment of inertia of a very thin hoop of
mass m and radius r about its symmetry axis.
Find the moment of inertia of a very thin hoop of
mass m and radius r about its symmetry axis. Consider a composite object, such as the two joined
disks in the figure on the right.
Consider a composite object, such as the two joined
disks in the figure on the right. Consider a wheel of radius r and mass m rolling on a flat surface in the
x-direction.
Consider a wheel of radius r and mass m rolling on a flat surface in the
x-direction. 
