Equilibrium of a rigid object

Assume two or more forces act on a rigid object.  The total force on the object is the sum of all the external forces.  According to Newton's third law, the sum of all the internal forces is zero.  We have F_tot = Ma_CM.
If the total force acting on the object is zero, the center of mass of the object will not accelerate.  The object is in translational equilibrium.  If the CM of the object is at rest, it will stay at rest, if it is moving with constant velocity, it will keep on moving with constant velocity.

For the object to be in rotational equilibrium, the total torque on the object must be zero.  The total torque on the object is the vector sum of all the external torques.  According to Newton's third law, the sum of all the internal torques is zero.

For an object to be in mechanical equilibrium, the net external force and the net external torque acting on the object have to be zero.

F_tot = 0,  τ_tot = 0.

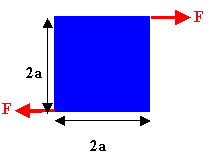The total torque can be nonzero, even though F_tot = 0.  Consider the situation shown in the figure on the right.  The square is initially at rest in the x-y plane.  The z-axis points out of the page.  The total force on the square is zero.  The CM of the square will stay at rest.  The total torque about the CM is not zero.  τ_tot = -2 √2 a F sin(45^o) k = -2aF k.
The square will have angular acceleration pointing into the page.

Two forces, equal in magnitude and opposite in direction, whose lines of action do not pass through the same center, are called a couple.  A couple produces a torque about the center.

No net external force implies that the center of mass of the object is at rest or moving with constant velocity.  No net external torque implies that the object either does not rotate or that it rotates with constant angular velocity.  For an object in mechanical equilibrium there exists some inertial reference frame in which the object's center of mass is at rest.  If in this frame the object also does not rotate, it is in static mechanical equilibrium.

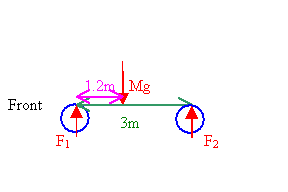Problem:

A 1500 kg automobile has a wheelbase (the distance between the axles) of 3 m.  The center of mass of the automobile is on the centerline at a point 1.2 m behind the front axle.  Find the force exerted by the ground on each wheel.

Solution:

• Reasoning:
  The car is in static equilibrium, F_tot = 0, τ_tot = 0.
• Details of the calculation:
  The force of gravity Mg acts on the center of mass of the object.  It produces no torque about the CM.
  F_tot = F₁ + F₂ - Mg = 0.
  τ_tot = F₂(1.8 m) - F₁(1.2 m) = 0.
  F₁ = 1.5 F₂.
  2.5 F₂ = Mg = 14700 N, F₂ = 5880 N.  F₁ = 8820 N.
  The force exerted by the ground on each rear wheel is F₂/2 = 2940 N and the force exerted by the ground on each front wheel is F₁/2 = 4410 N.

When an object is placed in a uniform gravitational field, then the force of gravity produces no torque about the center of mass of the object.  We can always represent the gravitational force as an arrow pointing straight towards or away from the center of mass of the object.  For this reason, the center of mass is also called the center of gravity of the object.

Equilibrium does not guaranty stability.

Example:

A ball and a bowl
The ball is in stable equilibrium at the bottom of a bowl.

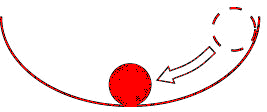
The ball is in unstable equilibrium at the top of a bowl.

Objects are in stable mechanical equilibrium if their potential energy increases when they are slightly disturbed.

An object in static equilibrium has static translational stability, if, when displaced from its equilibrium position by a small amount, a restoring force accelerates it back towards the equilibrium position.

An object in static equilibrium has static rotational stability, if, when rotated away from its equilibrium orientation through a small angle, a restoring torque results in angular acceleration back towards the equilibrium orientation.

An object has static rotational stability if its center of gravity is located above its base of support.  A minimum of 3 non-collinear contact points form a base.

When an object with static stability is disturbed too much, the limit of static stability can be reached.  The limit of static rotational stability is reached when the object's center of gravity is no longer located over its base of support.

A tricycle has a base with 3 contact points.  It has has static rotational stability.

A bicycle has only 2 contact points.  It is statically unstable and tips over easily.