For motion with constant angular acceleration α = (ω_f - ω_i)/(t_f - t_i) = Δω/Δt we have
Δω = ωΔt,  ω_f = ω_i + αΔt.
This is a vector equation.  It yields an equation for each Cartesian component.
For the z-component we have
ω_zf = ω_zi + α_zΔt.

If an object is rotating about the z-axis, and there are no other components of ω and α, we often drop the index z and just write
ω_f = ω_i + αΔt.

The angular displacement θ about the z-axis is then given by
∆θ = ∫_ti^tf (dθ/dt)dt =  ∫_ti^tf ωdt = ω_i(t_f - t_i) + ½ α (t_f - t_i)².

Kinematic equations for motion with constant angular acceleration

If an object is rotating about a fixed z-axis with constant angular acceleration α, we have Δω = αΔt,

ω_f = ω_i + α(t_f - t_i).

The angular displacement θ about the z-axis is then given by

θ_f = θ_i + ω_i(t_f - t_i) +  ½α(t_f - t_i)².

Combining these two equations we derive

ω_f² = ω_i² + 2α(θ_f - θ_i).

These equations are of the same form as the equations for linear motion with constant acceleration a. 
For motion along the x-axis we have

v_f = v_i + a(t_f - t_i),
x_f - x_i = v_x(t_f - t_i) + ½a(t_f - t_i)².
v_f² = v_i² + 2a(x_f - x_i).

If we replace x by θ and a by α, then the kinematic equations for linear motion along the x-axis transform into the kinematic equations for rotational motion about the z-axis.

With our definitions of angular position, velocity, and acceleration, we have kinematic equations for rotational motions that have the same form as the kinematic equations for translational motion.  And the same equations have the same solutions.  We solve them in exactly the same way.  But the solutions describe different physical situations.  For example, while θ_f can take on any value, a value that does not lie between 0 and 2π radians just tells us that the object has completed more than one revolution.

Problem:

An airliner arrives at the terminal and the engines are shut off.  The rotor of one of the engines has an initial clockwise angular speed of 2000 rad/s.  The engines rotation slows with an angular acceleration of magnitude 80 rad/s².
(a)  Determine the angular speed after 10 s.
(b)  How long does it take the rotor to come to rest?

Solution:

• Reasoning:
  In this problem the initial angular velocity ω_i and the angular acceleration α are given.  If we choose the direction of the initial angular acceleration to be the z-direction, then
  ω_f = ω_i - α(t_f - t_i),
  since α is in the negative z-direction. 
• Details of the calculations
  (a)  At t = 0, ω_i = 2000/s.
  At t = 10 s we have ω_f  = 2000/s - (80/s²)(10 s) = 1200/s.
  (b) Setting ω_f = ω_i - α(t_f - t_i) = 0 we can find the time it takes the rotor to come to rest.
  2000/s - (80/s²)t = 0,  t = (2000/80) s = 25 s is the time it takes the rotor to come to rest.

Problem:

A rotating wheel requires 3 s to rotate 37 revolutions.  Its angular velocity at the end of the 3 s interval is 98 rad/s.  What is the constant angular acceleration of the wheel?

Solution:

• Reasoning:
  Given:  Δθ = θ_f - θ_i = 37 revolutions,  Δt = 3 s,  ω_f = 98 rad/s.
  Using θ_f - θ_i = ω_i(t_f - t_i) + ½α(t_f - t_i)² and ω_f = ω_i + α(t_f - t_i), we have two equations, which we can solve for the two unknowns, ω_i and α.
• Details of the calculation:
  Using θ_f = θ_i + ω_i(t_f - t_i) + ½α(t_f - t_i)² with θ_i = 0, we have 37*2π = ω_i*(3 s) + ½α(3 s)².
  Using ω_f = ω_i + α(t_f - t_i) we have 98/s = ω_i + α(3 s).
  We solve this equation for ω_i  ω_i = 98 s - α(3 s), and insert it into the first equation.
  37*2π = (98/s)(3 s) - α(3 s)² + ½α(3 s)², 74π = 294 - α*(9 s²) + α*(4.5 s²),
  (4.5 s²)*α = 294 - 74π, α = 13.67/s² is the constant acceleration of the wheel.

Module 8: Question 1

The kinematic equations for motion with constant linear acceleration and motion with constant angular acceleration have the same form.  Compare motion with constant velocity with motion with constant angular velocity.

Discuss this with your fellow students in the discussion forum!

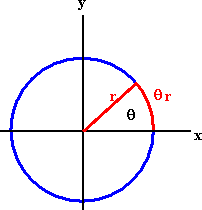When a wheel rotates about the z-axis, each point on the wheel has the same angular speed.  The linear speed v of a point P, however, depends on its distance from the axis of rotation. 
When a point P goes through an angular displacement of 2π, then its distance traveled is s = 2πr.
When a point P goes through an angular displacement of π, then its distance traveled is s = πr.
When a point P goes through an angular displacement of θ, then its distance traveled is s = θr.
In terms of the angular speed ω, the speed v of the point P therefore is

v = ds/dt = rdθ/dt = rω,

if r is constant; v is the tangential velocity of the point P.

Link:  Tangential and angular speed  (Youtube)

The tangential acceleration a of a point P moving along a circular path is given in terms of its angular acceleration by a_t = dv/dt = rdω/dt = rα.
The radial or centripetal acceleration is a_r = v²/r = rω².
The total acceleration is given by
a = (a_t² + a_r²)^½ = (r²α² + r²ω⁴)^½ = r(α² + ω⁴)^½.

Problem:

If a car's wheels are replaced with wheels of a larger diameter, will the reading of the speedometer change?  Explain!

Solution:

• Reasoning:
  The sensor for the speedometer senses the angular speed of the wheel.  Using v_nominal = r_nominalω, the speedometer displays the correct speed if the tires have the nominal radius.  If you put larger tires on your car, then your actual speed v_actual = r_actualω is greater than the displayed speed v_nominal = r_nominalω.

Problem:

A car accelerates uniformly from rest and reaches a speed of 22 m/s in 9 s  If the diameter of a tire is 58 cm, find
(a)  the number of revolutions the tire makes during this motion, assuming no slipping, and
(b)  the final rotational speed of the tire in revolutions per second.

Solution:

• Reasoning:
  The uniform acceleration of the car a = Δv/Δt is given.  We can use the kinematic equations for linear motion to find the distance it travels in the time interval Δt.
  Dividing this distance by the circumference of the tire, we find the number of revolution made.  The final angular speed is given by ω_f = v_f/r_tire.
• Details of the calculation:
  (a)  The acceleration of the car is a = Δv/Δt = (22 m/s)/(9 s) = 2.44 m/s².
  The distance traveled in 9 s is d = ½at² = (½*2.44*81) m = 99 m.
  The circumference of the tire is π*0.58 m = 1.82 m.
  The number of revolution made by the wheel is 99/1.82 = 54.3.
  (b)  The final linear speed of the tire is v = 22 m/s.  Using v = ωr, ω = v/r the final angular speed is ω = 75.9/s.  The number of revolutions per second is ω/2π = 12/s.