Assume that you are replacing the bearings in the wheel of your bicycle.  To test if you have done a good job, you hold the axle vertically and give it a spin.  The axle at the center of the wheel is stationary.  The wheel as a whole has no translational motion.  But the wheel is turning around the axle.  Every point on the wheel undergoes circular motion about an axis of rotation.  Such motion around an axis of rotation is called rotational motion.

Extended object can have translational and rotational motion.  Any motion of an extended object can be viewed as a combination of translational motion of the center of mass and rotational motion about the center of mass.

Sponge Toss Movie                  

Example:

A foam square has a blue LED near its CM and a red LED near its edge.  If we toss the sponge we can easily observe the parabolic motion of the CM and the rotational motion about the CM.

How do we describe rotational motion?

Assume you make a chalk mark on the rim of the wheel and you originally orient the wheel so that the chalk mark is facing you.  This is your reference orientation.  The angular position of the wheel describes its orientation relative to this reference orientation.  As the wheel rotates, this angular position is changing.  The angular displacement measures how far it has rotated from its reference orientation.  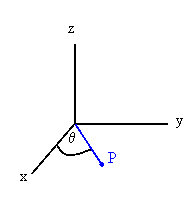It is often convenient to orient a coordinate system such that the z-axis coincides with the axis of rotation and the x-axis defines the reference orientation.  Then the angular displacement θ of a point P on the wheel is the angle θ a line from the axis of rotation to the point P makes with the x-axis.

Angles can be measured in units of degrees or radians.  360 degrees = 2π radians.  When describing rotational motion it is most convenient to measure angles in units of radians. 
To find out how fast the wheel is rotating, we measure its angular speed ω.  The average angular speed is given by

ω_avg = (θ_f - θ_i)/(t_f - t_i) = Δθ/Δt.

Every point on the wheel has the same angular speed.  The units of angular speed are rad/s or s^-1, because radians are not dimensional.

Assume that you turn the axle of the spinning wheel from vertical to horizontal.  The wheel is still spinning with the same angular speed, but its angular velocity ω has changed.  Angular velocity is a has magnitude and direction.  Its magnitude is the angular speed, and its direction is the direction of the axis of rotation.  There is, however, a subtlety we have to take care of.  Assume that the axis of rotation is vertical.  What is the sense of rotation?  Is the wheel spinning clockwise or counterclockwise as viewed from above?  Just saying the axis is vertical does not tell us the sense of rotation. 

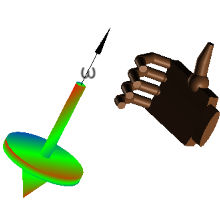
To specify the sense of rotation we use a convention called the right-hand rule.  If the fingers of your right hand are curling to indicate which way the wheel is turning, then the thumb of you right hand is pointing in the direction of the axis of rotation.  This is the direction of the angular velocity ω.

Please click on the image below for a 3-dimensional view!

Problem:

What is the average angular speed, in radians per second, of
(a)  the Earth in its orbit about the Sun, and
(b)  the Moon in its orbit about the Earth?

Solution:

• Reasoning:
  The earth orbits the sun once every year.
  The moon orbits the earth once 27.3 days
• Details of the calculation:
  (a)  The angular speed of the earth in its orbit about the sun is ω = 2π/year = 2π/(365*24*60*60 s) = 2*10^-7/s. 
  (b)  The angular speed of the moon in its orbit about the earth is ω = 2π/(27.3 days) = 2π/(27.3*24*60*60 s) = 2.7*10^-6/s.

Angular acceleration

The angular acceleration α is defined as the rate of change of the angular velocity.  The average angular acceleration is given by

α = (ω₂ - ω₁)/(t₂ - t₁) = Δω/Δt.

The angular velocity changes when the rotation rate is increasing or decreasing and when the axis of rotation changes direction.  The angular acceleration is a vector.

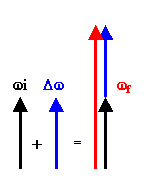If we change the number of revolutions the wheel makes per second, then each point on the wheel has angular acceleration.  Assume the angular velocity points in the z-direction, and over a one second time interval we change the angular speed of the wheel from π/s to 2π/s. The average angular acceleration is
α = (ω₂ - ω₁)/(t₂ - t₁) = ((2π/s - π/s) k/(1s) = (π/s²)k,
i.e. it has magnitude π/s and points in the z-direction.

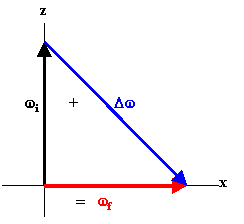If we turn the axis of rotation from vertical to horizontal, then each point on the wheel has angular acceleration.  Assume the wheel is rotating with angular velocity (2π/s)k about the z-axis.  If over a time interval of 1 s we reorient the axis of rotation from vertical to horizontal, so that the wheel is now rotating with angular velocity (2π/s)i about the x-axis, then the average angular acceleration is given by
α = (ω₂ - ω₁)/(t₂ - t₁) = ((2π/s i - 2π/s k) /(1s). 
The magnitude is (√2)2π and its direction makes an angle of 315^o with the x-axis.

Problem:

What is the magnitude of the angular velocity, ω, of the second hand of a clock?  What is the direction of ω as you view a clock hanging vertically?  What is the magnitude of the angular acceleration of the second hand?

Solution:

• Reasoning:
  The second hand of a clock goes through an angular displacement of 2π in one minute.  Its angular speed is ω = 2π/(60 s) = 0.105/s.  The direction of ω is perpendicular to the face of the clock, pointing into the face of the clock.  The average angular acceleration of the second hand is zero.