An object whose position as a function of time varies as
x(t) = Acos(ωt) exhibits simple harmonic motion.
The velocity of the object as a function of time is given by
v(t) = -ωAsin(ωt), and the acceleration is given by
a(t) = -ω²Acos(ωt) = -ω²x.

Simple harmonic motion is accelerated motion.  If an object exhibits simple harmonic motion if it is acted on by a restoring force F = -kx, with k = mω².  A mass oscillating on a spring is an example of an object moving with simple harmonic motion.

The pendulum:

Most system which have an equilibrium position execute simple harmonic motion about this position when they are displaced from equilibrium, as long as the displacements are small.  The restoring forces approximately obey Hooke's law.  However, for larger displacements the systems become anharmonic oscillators, i.e. the restoring forces are no longer proportional to the displacements.  The period then depends on the amplitude.  A familiar example of such a system is the simple pendulum.

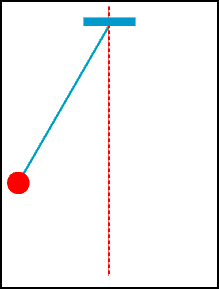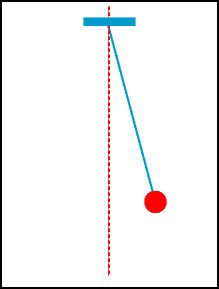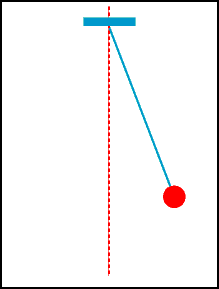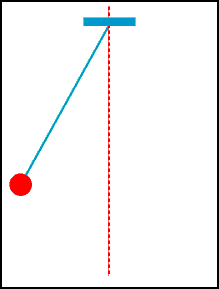An ideal simple pendulum consists of a point mass m suspended from a support by a massless string of length L.  (A good approximation is a small mass, for example a sphere with a diameter much smaller than L, suspended from a light string.)  The equilibrium position of the mass is a distance L below the support.  If the mass is displaced from its equilibrium position while keeping the string taut, it exhibits periodic motion, moving in a vertical plane along a circular arc.

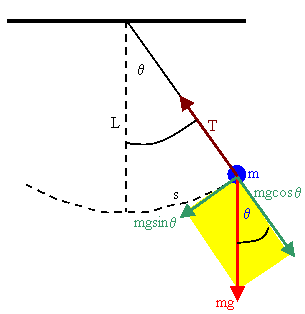
When the string makes an angle θ with the vertical, then the displacement of the mass from its equilibrium position along the circular arc is s = Lθ.  The forces acting on the mass are gravity and the tension in the string.  Only gravity provides a restoring force towards the equilibrium position.  The magnitude of this force is m g sinθ.  The equation of motion, F = ma, therefore yields

m d²s/dt² = m g sinθ,
or
d²θ/dt² = -(g/L) sinθ.

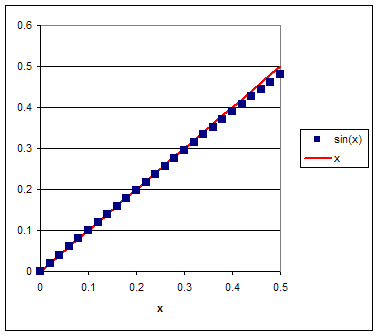The solution to this equation describes periodic, but not simple harmonic motion.
However, when the displacement from equilibrium is small, then sinθ ~ θ in radians.  (See graph.)
Then the equation of motion becomes

d²θ/dt² = -(g/L)θ.

The solution to this equation is θ(t) = θ_maxcos(ωt + φ), with ω² = g/L.

For small oscillations the period of a simple pendulum therefore is given by T = 2π/ω = 2π√(L/g).
It is independent of the mass m of the bob.  It depends only on the strength of the gravitational acceleration g and the length of the string L.  By measuring the length and the period of a simple pendulum we can determine g.

We can also write the equation of motion in terms of the displacement s = Lθ.
The net force acting on a simple pendulum bob with mass m is F= -mgsinθ.  It is a restoring force.  The displacement from the equilibrium position is s = Lθ.  When the displacement from equilibrium is small, then sinθ ~ θ in radians.  Then F = -mgθ = -mgs/L. 
The force obeys Hooke's law,  F = -ks, with k = mg/L.
m d²s/dt² =  -mgs/L,  d²s/dt² =  -(g/L)s.
The pendulum executes simple harmonic motion with ω² = g/L.

Problem:

The angular displacement of a pendulum is represented by the equation θ = 0.32*cos(ωt) where θ is in radians and  ω = 4.43 rad/s.  Determine the period and length of the pendulum.

Solution:

• Reasoning:
  θ(t) = θ_maxcos(ωt + φ) for small oscillations. 
• Details of the calculation:
  Here ω = 4.43/s, ω² = g/L = 19.62/s², L = 0.5 m.
  T = 2π/ω = 1.42 s

Problem:

A simple pendulum on a cuckoo clock is 5.00 cm long.  What is its frequency?

Solution:

• Reasoning:
  For a simple pendulum ω² = g/L.
• Details of the calculation:
  f = 1/T = ω/(2π) = (g/L)^1/2/(2π) = 2.23/s.

Problem:

A simple pendulum with a period of 2.00000 s in one location where g = 9.80 m/s² is moved to a new location where the period is now 1.99796 s.  What is the acceleration due to gravity at its new location?

Solution:

• Reasoning:
  For a simple pendulum the period T = 2π)/ω is proportional to 1/g^1/2.
• Details of the calculation:
  T_old/T_new = (g_new/g_old)^1/2.  g_new = g_old*(T_old/T_new) = 9.8*(2/1.99796)² = 9.82 m/s².

Problem:

Pendulum clocks are made to run at the correct rate by adjusting the pendulum's length.  Suppose you move from one city to another where the acceleration due to gravity is slightly greater, taking your pendulum clock with you, will you have to lengthen or shorten the pendulum to keep the correct time, other factors remaining constant?

Solution:

• Reasoning:
  For a simple pendulum the period T is proportional to (L/g)^1/2.  If g increases slightly, L has to increase slightly to keep the period the same.  You will have to lengthen the pendulum.

Link:  A simple pendulum

The pendulum wave

Please watch these Youtube videos in lieu of demonstrations.

• Pendulum Waves
• Giant pendulum wave

How does the pendulum wave work?

Assume you have 15 pendulums.
You can choose the period or frequency for each pendulum by choosing its length.  T = 2π(L/g)1/2,  f = (1/2π)(g/L)1/2.
A shorter length corresponds to a higher frequency.

Example:

Chose the length of the longest pendulum so that its frequency is f = 52/min.
Make the next pendulum slightly shorter, so its frequency is f = 53/min.
Continue to make the pendulums shorter so that their frequencies become 54/min, 55/min, ..., 66/min. 
(The 15th pendulum has a frequency of (52 + 14)/min = 66/min.)
After 1 minute all pendulums have completed an integer number of oscillations and returned to their initial position.

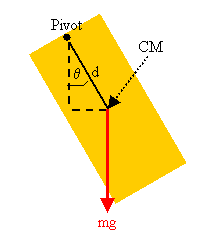A physical pendulum is an object suspended in a uniform gravitational field from a point other than its center of mass.  The object can rotate about an axis through the suspension point.  When the CM is displaced from its stable equilibrium point under the support, the gravitational force exerts a torque about the support, resulting in angular acceleration.  The CM accelerates towards its equilibrium position.  The object exhibits periodic motion.  For small displacements, when sinθ ~ θ, the motion is simple harmonic, θ(t) = θ_maxcos(ωt + φ), with ω² = (mgd)/I and the equilibrium position chosen to be zero.  Here I is the moment of inertia of the object about the axis of rotation through the support and d is the perpendicular distance of the CM from the axis of rotation through the support.