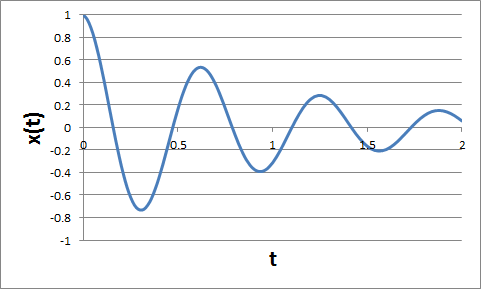
Example: m = 1, k = 100, b = 1
Example: m = 1, k = 100, b = 1
Friction will damp out the oscillations of a macroscopic system, unless the oscillator is driven. If the speed of a mass on a spring is low, then the drag force R due to air resistance is approximately proportional to the speed, R = -bv. The total force on the object then is
F = -kx - bv.
The equation of motion, F = ma, becomes md2x/dt2 = -kx - bdx/dt.
The solution to this differential equation is
x(t) = Aexp(-bt/2m)cos(ωdampt + φ),
with ωdamp2 = k/m - (b/2m)2,
as long as b2 < 4mk, i.e. as long as the drag force is not too large. The oscillatory character of the motion is preserved, but the amplitude decreases with time.
The amplitude of a lightly damped oscillator decreases by 5% during each cycle. What percentage of the mechanical energy of the oscillator is lost in each cycle?
Solution:
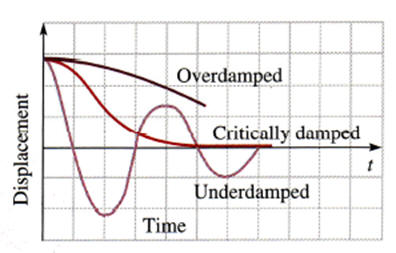If
the drag force is and b2 ≥ 4mk, then oscillatory character of
the motion is n longer preserved, and the motion is critically damped or
overdamped.
How would a car bounce after a bump under each of these conditions?
(a) overdamping
(b) underdamping
(c) critical damping
Discuss this with your fellow students in the discussion forum!
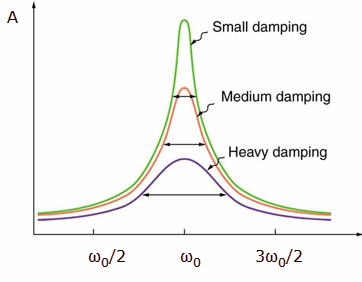
Amplitude versus driving frequency
A driving force with the natural resonance frequency of the oscillator can
efficiently pump energy into the system.
Assume a driving force F = F0cosωextt.
The total force on the object then is F = F0cos(ωextt) - kx - bv.
The equation of motion, F = ma, becomes md2x/dt2
= F0cos(ωextt)
- kx - bdx/dt.
After a steady state has been reached, the position varies as a function of time as
x(t) = Acos(ωt + φ).
Here ω = ωext is the angular frequency of the driving force. The amplitude of the motion is given by
A = (F0/m)/[(ω02 - ω2)2 + (bω/m)2]½,
where ω02 = k/m. ω0 is he natural frequency of the undamped oscillator. When the frequency of the driving force is very close to the natural frequency and the drag force is small, then the denominator in the above expression becomes very small, and the amplitude becomes very large. This dramatic increase in amplitude is called resonance, ω = ω0 is called the resonance frequency.
Calculate the resonance frequency of
(a) a 3 kg mass attached to a spring of force
constant 240 N/m and
(b) a simple pendulum 1.5 m in length.
Solution:
If we push a child on a swing once during each period, and we always push in
the same direction, we will increase the amplitude of the swing, until the
positive work we do on the swing equals the negative work done on the swing by
the frictional forces.
If we drive a harmonic oscillator with a driving force with the natural
resonance frequency of the oscillator, then the amplitude can increase
enormously, even if the work done during each cycle is very small. The
amplitude of an ideal harmonic oscillator increases forever. Friction limits
the maximum amplitude of a real oscillator. The amplitude may become large
enough for the system to become an anharmonic oscillator. Then the driving
force is no longer in phase with the
oscillations, and it sometimes does negative work and reduces the amplitude.
Often, however the amount of energy put into the system is large enough to
damage or break the system.
Some engineers use sound to diagnose performance problems with car engines. Occasionally, a part of the engine is designed that resonates at the frequency of the engine. The unwanted oscillations can cause noise that irritates the driver or could lead to the part failing prematurely. In one case, a part was located that had a length L made of a material with a mass M. What can be done to correct this problem?
Discuss this with your fellow students in the discussion forum!
Links: