Objective:

In this laboratory you will determine the density of a metal block by applying Archimedes' principle.  Then you will determine the viscosity of a brand of "Volumizing Shampoo" using Stokes' law.  You will use a fluid column as a viscometer and measure the rate of descent of a steel sphere, as it falls under the influence of gravity through the fluid, after the sphere has reached terminal velocity.

Experiment 1: 

Archimedes' Principle states that an object partially or wholly immersed in a gas or liquid is acted upon by an upward buoyant force B equal to the weight w of the gas or liquid it displaces.  In this experiment you will verify this by measuring the apparent loss of weight of several submerged objects and by finding the weight of the displaced fluid.  You will also determine the density of the objects.  A PASCO Force Sensor is used to measure the weights.

Equipment that was used to produce the experimental data below:

• Force Sensor
• Two containers, one with and one without overflow spout
• Various solid objects

Procedure:

I.  Verify Archimedes' principle using the data below.  Click on a small picture if you want to see an enlarged picture.

	(a)	(b)	(c)	(d)
Object 1:
Object 2:
Object 3:
Object 4:

For each of the objects:

(a)  Determine the weight W_c of the empty container with the handle.  When the container is suspended from the force sensor, the force sensor measures the force of gravity (weight) acting on the object, and the program displays the magnitude of this force (in N) on the computer screen.

(b)  Determine the weight of an object W_o when it is suspended above the container with the overflow spout.  This container is completely filled with water, and the container with the handle standing below the spout is empty.

(c)  Determine the apparent weight of the object W_ow after it has been lowered into the water.  As the object is lowered into the water, water pours out of the overflow spout.  The container with the handle has collected this water.

(d)  Determine the weight W_cw of the container with the handle holding the collected water.

Record the weights in a spreadsheet as shown below.

For each of the objects:

• Calculate the weight of the water that was displaced.  W_w = W_cw- W_c.  Record it in the spreadsheet.
• Calculate the difference between the weight of the object in air and its apparent weight in water.  This difference yields the buoyant force F_b.  F_b  =  W_o - W_ow.  Record F_b in the spreadsheet.
• Compare F_b and W_w.  Calculate the percent difference = 100%(F_b - W_w)/F_b and record it in the spreadsheet.

II.  Determine the density of the objects.

Extend your Excel spreadsheet.  Set up labels as shown below.

• Determine the mass m_o of each objects by dividing its weight by the acceleration due to gravity and record it in the spreadsheet.
• From the weight of the water displaced by the object calculate its mass m_w and record it in the spreadsheet.
• Use the density of water, 1000 kg/m³, and the mass of the displaced water, to calculate the volume V_w of the displaced water.  Record this volume in the spreadsheet.
• The volume of the displaced water is the same as the volume of the object.  Calculate the density ρ_o of the object  (ρ = m/V) and record it in the spreadsheet.
• Compare the density you found with the density of the materials ρ_t given in the table below.  Try to identify the material each object is made of.  If you cannot identify the material based on the density alone, also consider the appearance of the material.  (Brass and steel have a different color.)

Log entries:

• Show your spreadsheet entries from part I and part II. 
• Answer the following questions:
  According to Archimedes' principle, the buoyant force is equal to the weight of the displaced fluid.  Do your experimental results verify Archimedes' principle?  Comment on your results.
  Do your experimentally determined densities of the various materials agree with the densities given in the table?  Comment on your results.

Viscosity

Viscosity is a measure of a fluids resistance to relative motion within the fluid.  Highly viscous fluids do not readily flow.  The viscosity of a fluid usually varies with temperature.  For a fluid flowing through a pipe in laminar flow, viscosity is one of the factors determining the volume flow rate.

Poiseuille's law: Q = π∆Pr⁴/(8ηL)

Volume flow rate = π*(pressure difference)*(pipe radius)⁴/[8*(pipe length)*viscosity)

Exercise

Blood is a viscous fluid circulating through the human body.  The circulatory system is a closed-loop system with two pumps.  One-way valves keep the flow unidirectional.  A sketch is shown below.  The unit of pressure in the sketch is mm Hg.  (1 atm = 760 mm Hg)

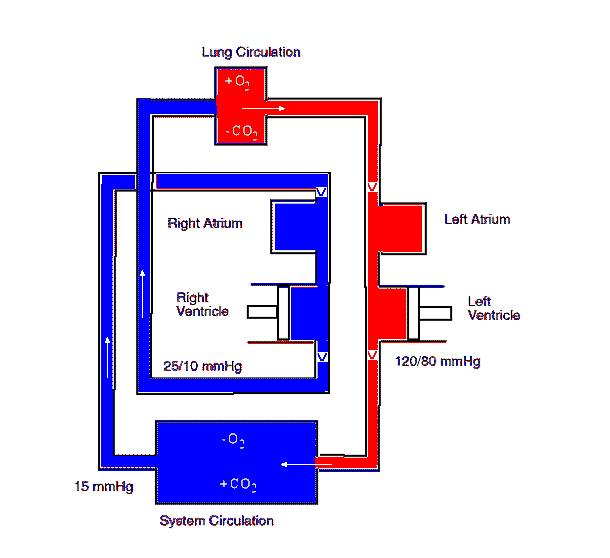
During heavy exercise, the blood's volume flow rate is 5-10 times higher than when the body is at rest.  Discuss different possible ways that a body can accomplish this?

• Is increasing blood pressure 5 - 10 times higher a viable option?  What percentage increase in blood pressure is reasonable?  Explain!
• Is decreasing the length of your blood vessels a viable option?  Explain!
• The arterioles (small arteries) are surrounded by circular muscles. 
  
  In order to increase the blood flow rate by a factor of 5, what percentage increase in the radius of a blood vessel is needed?  (This is called vasodilatation.)
• Arteries in the human body can be constricted when plaque builds up on the inside walls.  How does this affect the blood flow rate through this artery?  Is it possible for the body to keep the flow rate constant?  Explain!

It is often important to know the viscosity of a fluid.  A viscosimeter is the instrument used to measure viscosity.  The study of the viscosity of substances is known as rheology.

Example:

In order to keep the pistons moving smoothly in the cylinders of the internal combustion engine in a car, a thin film of motor oil between the piston rings and the cylinder wall acts as a lubricant.  The oil must be able to keep the piston moving smoothly, when the engine first starts up and is still cold and when the engine reaches its high operating temperature.  One way of measuring an oil's ability to lubricate is to measure its viscosity.

In this session you will determine the viscosity of different brands of "Volumizing Shampoo" using Stokes' law.  You will use a fluid column as a viscometer and measure the rate of descent of a steel sphere, as it falls under the influence of gravity through the fluid, after the sphere has reached terminal velocity.

George Gabriel Stokes, an Irish-born mathematician, worked most of his professional life describing fluid properties.  Stokes' law gives the force required to move a sphere through a viscous fluid at a specific velocity, as long as the flow around the sphere is laminar and the Reynolds number is low (Reynolds number < 1).  Stokes' Law is written as

F = 6πηrv.

Here r is the radius of the sphere, v the speed and η the viscosity. 

Experiment 2:

Procedure:

Measure the rate of descent of a steel sphere, as it falls under the influence of gravity through the shampoo.

  

Do the experiment!  Find the speed (positive number) of the sphere.

• Insert your data table and your plot of position versus time (with trendline) into your log.

Data Analysis:

The forces acting on the sphere are gravity, the buoyant force, and the viscous drag force given by Stokes' law.  A free body diagram is shown below.

Since the sphere moves with constant velocity, the net force is zero. 

• F_drag + F_buoyant = mg
• 6πηr_spherev + ρ_fluidV_sphereg = ρ_sphereV_sphereg
• 6πηr_spherev + (4/3)πρ_fluid(r_sphere)³g = (4/3)πρ_sphere(r_sphere)³g
• η = 2(ρ_sphere - ρ_fluid)(r_sphere)²g/(9 v)

The density of the "Volumizing Shampoo" is very close to that of water, ρ_fluid = 1.03 g/cm³.
The density of the stainless steel ball is 7.866 g/cm³, and its diameter is 1/4 inch = 0.635 cm.

• Calculate the viscosity η of the shampoo using your measured velocity in units of poise = g/(cm-s). 
  Use the densities in units of g/cm³, the speed in units of cm/s, the radius of the sphere in units of cm and g = 981 cm/s².
  (1 Pa-s = 1 kg/(m s) = 10 g/(cm-s) = 10 poise)
• Calculate the Reynolds number  R = 2ρ_fluidr_spherev/η.  It is a dimensionless number.
  Check that the Reynolds number is less than 1, so that we are in the regime where Stokes' law is valid.
• The table below lists typical viscosities of some viscous fluids at room temperature.  Does your value for the viscosity of the shampoo seem reasonable?  Discuss.

• Predict the terminal velocity of a sphere made of the same material but with diameter of 3/8 inch in the same fluid.  One group should measure it.

Convert your log into a lab report.  See the grading scheme for all lab reports.

Name:
E-mail address:

Laboratory 1 Report

• In one or two sentences, state the goal of this lab.
• Make sure you completed the entire lab and answered all parts.  Make sure you show your work and inserted and properly labeled relevant tables and plots.
• Add a reflection at the end of your report in a short essay format.

Save your Word document (your name_lab1.docx), go to Canvas, Assignments, Lab 1, and submit your document.