Objective:

In this lab you will investigate some thermometric properties of gases.  You will also experimentally investigate a change of phase of water.

Open a Microsoft Word document to keep a log of your experimental procedures, results and discussions.  Address the points highlighted in blue.  Answer all questions.

Changes of phase

Substances can exist in solid, liquid or gas phases.  At a constant pressure, changes of phase always occur at the same temperatures for any pure substance.

The temperature is a measure of the internal, disordered energy of a substance.  The absolute temperature of any substance is proportional to the average translational kinetic energy associated with the random motion of the molecules of the substance.

½m<v²> = (3/2)k_BT

In SI units the scale of absolute temperature is Kelvin (K).  But we use different temperature scales in everyday situations.  The Kelvin scale is identical to the Celsius (^oC) scale, except it is shifted so that 0 ^oC equals 273.15 K.

Discussion 1

Specific heat capacity

Consider the experiment described below.

A 1.0 kg mass and a 3.0 kg mass with different initial temperatures are placed together inside a well-insulated container and allowed to come to thermal equilibrium.  The insulated container prevents any transfer of energy to or from the environment (including the container itself).

Do you agree or disagree with the following statements?  Explain why you agree or disagree.

• (a)  Heat flows from the 1.0 kg mass to the 3.0 kg mass because the 1.0 kg mass has a much larger heat capacity.
• (b)  The thermal energy lost by the 3.0 kg mass is greater than the thermal energy gained by the 1.0 kg mass.

Experiment

The experiment starts by measuring the mass of a Styrofoam cup (and temperature sensor).  Then a quantity of hot water is added, and the temperature of the water and the mass of the cup and water is measured.  Then ice at its melting temperature (0 ^oC) is added until the temperature of the water drops to about 10 ^oC and all the ice has melted.  The final temperature of the water and the mass of the cup and water (initial and melted) is measured.
Note:  The scale shows the masses in gram.  It shows numbers with one digit behind the decimal point.

The mass of the cup is measured at room temperature.	Hot water has been added and the initial temperature Ti is measure.	Ice has been added and the final temperature Tf is measured.

Your task:

Determine the latent heat of fusion of ice/water using the measured masses and temperatures and value of the specific heat capacity of water.

Procedure:

• Record the mass of the Styrofoam cup in a table in Excel.
• Record the mass of the cup and the hot water.
• Record the initial temperature T_i of the water.
• Record the mass of the cup-water-ice combination.
• Record the final temperature T_f of the water.

Data Analysis:

• The specific heat capacity of water is c_w = 1 kcal/(kg ^oC).
  When the water cools, the amount of heat released is ΔQ_released = c_wm_w(T_i - T_f).
• If no energy is exchanged with the environment, then the heat released by the water is absorbed by the ice. 
  It is used to melt the ice and raise the temperature of the resulting water to the final temperature of the measurement.
  The amount of heat absorbed by the ice is ΔQ_absorbed = L_fm_ice + c_wm_ice(T_f - 0 ^oC).
• Setting ΔQ_released = ΔQ_absorbed we have c_wm_w(T_i - T_f) = L_fm_ice + c_wm_ice(T_f - 0 ^oC).
  L_f = c_w(m_w/m_ice)(T_i - T_f) -  c_wT_f  (all temperatures in ^oC).
• Determine the latent heat of fusion, L_f, from your data and compare with the accepted value.  Paste your table into your Word document.

Discuss:

• What are some of the experimental errors that could cause your measured value of L_f to differ from the accepted value?
• Why is it important to dry the ice before adding it to the water?

Gas Properties

The ideal gas law states that for a fixed volume of an ideal gas (PV/T) = nR = constant.  Here P and V are the pressure and volume of the gas at absolute temperature T.  Theoretical derivations of the ideal gas law neglect the forces that the gas molecules exert on each other.  Real gases therefore do not strictly obey the ideal gas law.  However, at sufficiently low densities, intermolecular forces do not play a significant role and the ideal gas law becomes increasingly accurate.  For instance, at 20 atm pressure and room temperature, the volume of 1 mole of oxygen gas is about 2.3% smaller than predicted by the ideal gas law, but at 1 atm pressure the volume is only about 0.13% smaller. 

• If the temperature T is constant the ideal gas law yields Boyle's law, PV = constant (at constant T). 
• If the pressure is held constant, the ideal gas law yields Charles's law, V/T = constant (at constant P).

Remember:

If an equation in physics contains the temperature T, this temperature is always the absolute temperature.  In SI units it is always measured in K.  If an equation contains a temperature difference ΔT, this temperature difference can be measured in K or ^oC in SI units, since both scales give the same ΔT.

Exercise

Use an on-line simulation from the University of Colorado PhET group to verify Boyle's law and Charles' law.
Link to the simulation: Gas Properties

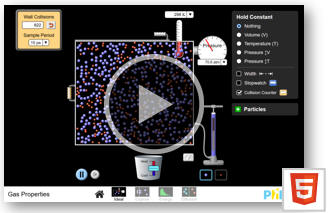
(a)  Click on the "Ideal" link.  Explore the interface!

• You can pump two types of molecules into the chamber.
• You can specify constant volume, pressure, or temperature.
• You can heat up or cool the gas in the chamber.
• You can use various measuring tools. (Explore what they can be used for.)

(b)  Reset the simulation, choose constant volume and add gas to the chamber at 300 K until the pressure is between 20 and 30 atm.
Switch to constant temperature and verify Boyle's law.  Boyle's law states  that PV = constant for constant T, or P = constant/V.
Vary the width of the box with the handle.
A plot of P versus 1/V should yield a straight line.  If it does, you have verified Boyle's Law.

Construct an appropriate data table and plot with at least 6 data points.  Paste them into your Word document.  Add comments.  Did you verify Boyle's law?
[The volume of the box is V = depth * height * width.  Depth and height are fixed, so  V = constant*width.  In the simulation the constant is 35 nm².  The width can be measured in units of nanometer (nm).]

(c)  Switch to constant pressure and verify Charles' law.  Charles' law states V = constant * T for constant P, where T is the absolute temperature.  A plot of V versus T should yield a straight line.  If it does, you have verified Charles' Law.

Construct an appropriate data table and plot with at least 6 data points.  Paste them into your Word document.  Add comments.  Did you verify Charles' law?

(d)  Click the energy link at the bottom of the simulation.   Explore the additional interface options!
Add two species gas to the chamber at 300 K until the pressure is between 40 and 50 atm. 

Compare the average kinetic energies of the two types of particles.  Explain your results.

Compare the average speeds of the two types of particles.  Explain your results.

Discussion 2

Regulating the temperature of the human body

The human body has the ability to regulate its temperature so that it remains very close to 37 ^oC.  If the body is overheating as a result of strenuous exercise, the surface blood vessels dilate to increase the blood flow to the surface areas.  Heat is carried by the blood to the surface where it causes the skin temperature to increase.  The body also begins to produce sweat.  The rate of sweating increases strongly with body temperature above 37^oC. 

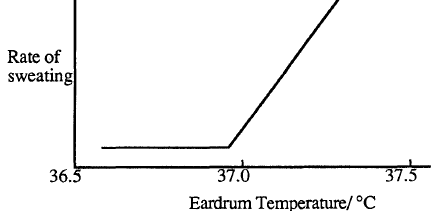
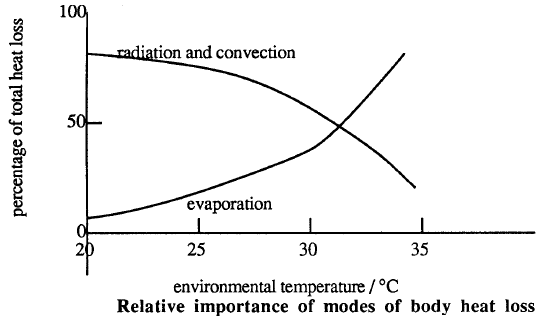
Conduction, evaporation, convection, and radiation can now transfer heat from the skin to the environment.  The chart below shows the relative importance of these heat transfer mechanisms at different environmental temperatures.

Questions:

• For environmental temperature below 32 ^oC, convection and radiation are the dominant heat removal mechanisms.  What can a person do to increase the amount of heat carried away by these mechanisms?
• Why is conduction usually not a dominant heat removal mechanism?  Can you think of situations when it becomes important?
• Why do convection and radiation no longer remove heat from the body at environmental temperature above 37 ^oC?

Evaporation

The body secrets water on to the skin from sweat glands.  As this water evaporates, the latent heat of vaporization is removed from the body.  The rate of evaporation increases as the degree of saturation of the surrounding air decreases.  In warm humid weather, the rate may be so low that a layer of water accumulates on the skin.  In still air, the air near the skin will become saturated and evaporation will stop.  Evaporation will increase if this saturated air is continually removed by wind or an artificially produced air stream.

Questions:

• If there is a cool wind blowing, what would be the consequences, as far as heat loss from the body is concerned, of wearing wet clothes?  Explain your answer.
• Cloudy nights are usually warmer than cloudless nights.  Why?

Convert your log into a lab report.  See the grading scheme for all lab reports.

Name:
E-mail address:

Laboratory 2 Report

• In one or two sentences, state the goal of this lab.
• Make sure you completed the entire lab and answered all parts.  Make sure you show your work and inserted and properly labeled relevant tables and plots.
• Add a reflection at the end of your report in a short essay format.

Save your Word document (your name_lab2.docx), go to Canvas, Assignments, Lab 2, and submit your document.