The building blocks of ordinary matter are atoms and molecules. Molecules are two or more atoms held together by a chemical bond. Atoms themselves are made up of more fundamental particles, i.e. protons, neutrons, and electrons. In a solid, the atoms and molecules are densely packed and held in place by intermolecular forces. The atoms in a solid can be modeled as being held together by tiny springs that permit them to vibrate back and forth about their equilibrium position, but not to exchange positions with other atoms. Solids are nearly incompressible. In a liquid the atoms and molecules are also densely packed. They cannot easily escape from one another, but they are free to move with respect to each other. Liquids are nearly incompressible. In a gas, intermolecular forces are weak and short ranged, and the atoms and molecules can move about nearly independently. Gases are compressible. Gases and liquids are fluids, i.e. collections of atoms or molecules that are free to move with respect to each other.
Assume a substance in a volume V has mass M and is made up of N particles.
We define the particle density ρparticle
as the number of particles per unit volume, ρparticle = N/V.
We define the density ρ of the substance as
its mass per unit volume, ρ = M/V.
A king orders a gold crown having a mass of 0.5 kg. When it arrives from the metal smith, the volume of the crown is found to be 185 cm3. Is the crown made of solid gold? The density of gold is 1.9*103 kg/m3.
Solution:
External link: Densities of various materials
We define the pressure P as the magnitude of the normal force F exerted over an area A, divided by the area A. Pressure equals force per unit area.
P = F/A
In SI units, the units of pressure are N/m2 = Pa (pascal).
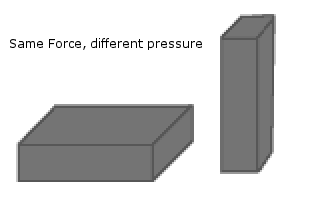A brick is at rest on a table. The force with which
the brick pushes on the table is its weight, F = mg. The pressure it
exerts on the contact area depends on the brick's orientation. If
the contact area between brick and table is larger, the brick exerts
less pressure on the contact area.
Grab a pencil with one hand and press the
flat end against your other hand. Press hard. Does it hurt?
Now turn the pencil around and press the tip of the pencil against
your other hand with the same force. Does it hurt now?
A 50 kg woman balances on one heel of a high-heel shoe. If the heel is circular with
radius 0.5 cm, the pressure she exert on
the floor is
P = F/A = (50 kg 9.8
m/s2)/(π(0.005 m)2) = 6.2*106 N/m2 = 6.2 MPa.
(1 MPa = 1000000 Pa)
If the woman wears a flat-heel shoe with a
radius of 3 cm then the pressure she exerts on the floor is
P
= F/A = (50 kg 9.8 m/s2)/(π(0.03 m)2) = 1.7*105N/m2 = 0.17 MPa.
The pressure she exerts is
reduced by a factor of 36. Be careful around women with high-heel shoes!
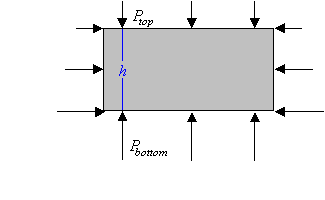
The pressure at a point below the surface of a liquid in a constant gravitational field depends only on the depth of that point and the pressure at the surface.
Any change in the pressure at the surface is therefore transmitted to every point in the liquid.
This is called Pascal's law.
Consider a large pool of water on the surface of the earth and a box-shaped volume of water at some depth in the pool. Imagine it enclosed by some weightless container.
The volume of water is in equilibrium and stays in place. It does not rise and it does not fall. The net force on it must be zero. The vertical component of the net force is
Fnet = PbottomA - PtopA - Mg = 0.
Fnet = PbottomA - PtopA - ρhAg = 0.
Pbottom - Ptop = ρhg.
The pressure in the pool increases with depth. If we let h denote the vertical distance of a point below the surface of the water, then we can write the pressure at this point as
Pbelow = Ptop + ρhg.
P is the pressure at depth h and P0 is the pressure at the surface. Very often this pressure is atmospheric pressure. The atmospheric pressure at sea level at room temperature is approximately
1 atmosphere = 101 kPa = 14.7 pounds per square inch (psi).
Gauge pressure is the pressure relative to atmospheric pressure. Gauge pressure is positive for pressures above atmospheric pressure, and negative for pressures below it. Absolute pressure is the sum of gauge pressure and atmospheric pressure.
Consider three drinking glasses. All three have the same area base, and all three are filled to the same depth with water. Glass A is wider at the top than at the bottom, glass B is cylindrical and so holds less water than A. Glass C is narrower at the top than at the bottom, and so holds less water than B. Which glass has the greatest liquid pressure at the bottom?
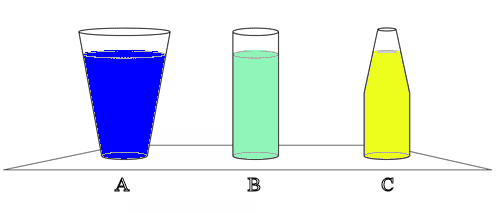
Solution:
Determine the absolute pressure at the bottom of a lake that is 30 m deep.
Solution:
The water pressure increases by approximately 1 atm for every 10 m increase in depth.
Intravenous infusions are usually made with the help of the gravitational force. Assume
that the density of the fluid being administered is very close to that
of water (1 g/cm3). At what height should the IV bag be placed
above the entry point so that the fluid just enters the vein if the
blood pressure in the vein is 18 torr = 2392 Pa above atmospheric
pressure? Assume that the IV bag is collapsible.
Solution:
What is the hydrostatic force on the back of Grand
Coulee Dam if the water in the reservoir is 150 m deep and the width of
the dam is 1200 m.
Solution:
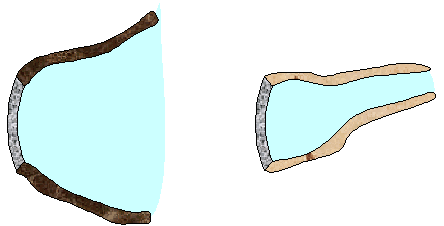The figure on the right shows an aerial view from
directly above two dams. Both dams are equally long and equally deep.
The dam on the left holds back a very large lake and the dam on the
right holds back a narrow river. Which dam has to be build more
strongly?
Solution:
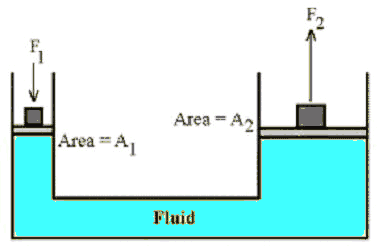A hydraulic system is used to lift a 2000 kg vehicle in an auto garage. If
the vehicle sits on a piston of area 0.5 m2, and a force is
applied to a piston of area 0.03 m2, what is the minimum
force that must be applied to lift the vehicle?
Solution:
Conservation of energy requires that the work done on the system
must balance the work done by the system. In the hydraulic
lift the distance over which F1 is applied is be greater
than the distance over which F2 acts by the exact same
ratio as the force multiplier.
F1/F2 = d2/d1.
Suppose the master cylinder in a hydraulic system is at a greater height than the cylinder it is controlling. Explain how this will affect the force produced at the cylinder that is being controlled.
Discuss this with your fellow students in the discussion forum!