Viscosity

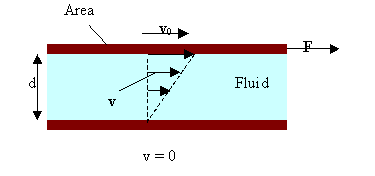
imageA real fluid flowing in a pipe experiences frictional forces.  There is friction with the walls of the pipe, and there is friction within the fluid itself, converting some of its kinetic energy into thermal energy.  The frictional forces that try to prevent different layers of fluid from sliding past each other are called viscous forces.  Viscosity is a measure of a fluids resistance to relative motion within the fluid.  We can measure the viscosity of a fluid by measuring the viscous drag between two plates.

If you measure the force to keep the upper plate moving with constant velocity v0, you find it is proportional to the area of the plate and to v0/d, where d is the distance between the plates.

F/A = ηv0/d  or  F/A = η∆v/∆y.

The proportional constant η is called the viscosity.  The units of η in SI units are Pa-s.  (Another common unit is poise (P).  1 Pa-s = 10 P.)

Examples:

Viscosity of air (20 oC): 1.83*10-5 Pa-s
Viscosity of water (20 oC): 1.0*10-3 Pa-s
Viscosity of honey (20 oC): ~1000 Pa-s

The viscosity of fluids depends strongly on temperature.

In liquids, viscosity is due to the cohesive forces between the molecules and in gases, viscosity is due to collisions between the molecules.  The work done by viscous forces converts ordered energy into thermal energy.  For a fluid flowing in a long horizontal pipe, the pressure drops along the pipe in the direction of the flow.  The faster the fluid is flowing, the larger is the pressure drop.

If the viscosity η is a constant, independent of flow speed, then the fluid is termed a Newtonian fluid.  When η does depend on the velocity of flow, then the fluid is called non-Newtonian or complex.  Blood is a mixture of a Newtonian and a non-Newtonian fluid.  It contains corpuscles and other suspended particles.  The corpuscles can deform and become preferentially oriented, so that the viscosity decreases with flow speed.  A corn starch-water mixture is another example of a non-Newtonian fluid.

External links:
Non-Newtonian Fluids (Youtube)
Fluid Dynamics: Non-Newtonian Fluids (Youtube)

Under all circumstances where it has been experimentally checked, the velocity of a real fluid goes to zero at the surface of a solid object.

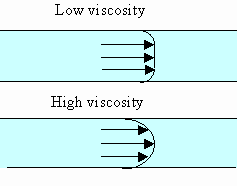imageA thin layer of fluid next to the walls of the pipe does not move at all.  The speed of the fluid increases with distance from the walls of the pipe.  If the viscosity of the fluid is low or the pipe has a large diameter, a large central region will flow with uniform velocity.  For a high viscosity fluid the transition takes place over a large distance and in a small diameter pipe the velocity may vary throughout the pipe.

If a viscous fluid such as water is flowing smoothly through the pipe, it is in laminar flow.  The velocity at a given point does not change in magnitude and direction.  The water is flowing in a steady state.  A small volume of fluid follows a streamline, and different streamlines do not cross. 

The rate at which a fluid flows through a hose or a pipe is proportional to

These relationships are expressed in terms of an equation known as Poiseuille's law.

Volume flow rate = π*(pressure difference)*(pipe radius)4/[8*(pipe length)*viscosity)
or
Q = π∆Pr4/(8ηL)

Problem:

The diameter of a pipe is doubled while the pressure difference across the pipe remains the same.  By what factor does the volume flow rate of the pipe change?

Solution:

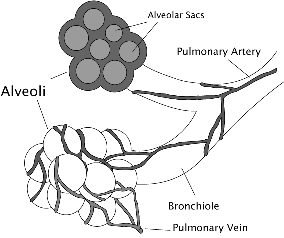imageThe volume flow rate through a pipe is strongly dependent on the pipe radius, Q ∝ r4.  This becomes important on many different situations.  In our respiratory system the flow of gas is Poiseuillean.  The resistance to flow is primarily determined by the narrow tubes or bronchioles leading to the alveoli.  Any narrowing of those tubes, for example a bronchospasm or sudden constriction of the muscles in the walls of the bronchioles, increases the resistance to flow and makes breathing much more difficult.

In the circulatory system the blood's pressure is highest when the blood leaves the heart and lowest when it returns to the heart.  Most loss of pressure occurs over the capillaries.  Any constriction, for example a build-up of cholesterol on the walls of the arteries, increases the resistance and hence the pressure drop, ∆P ∝ 1/r4.  So the heart has to work much harder to maintain the volume flow rate.  When an increased flow rate is required because of stress, a breakdown becomes more likely.

Problem:

An intravenous (IV) system is supplying saline solution to a patient at the rate of 0.1 cm3/s through a needle of radius 0.2 mm and length 5 cm.  What gauge pressure is needed at the entrance of the needle to cause this flow?  Assume that the viscosity of the saline solution to be the same as that of water, η = 1.0*10-3 Pa-s, and that the gauge pressure of the blood in the vein is 1500 Pa.

Solution:

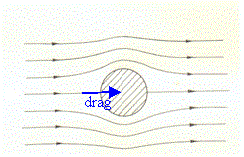imageIf a fluid in laminar flow flows around an obstacle, it exerts a viscous drag on the obstacle.  Frictional forces accelerate the fluid backward (against the direction of flow) and the obstacle forward (in the direction of flow).  The viscous drag force increases linearly with the speed of the fluid.

While flying in an open cockpit airplane, you feel the air rushing past you.  A person on the ground observes you moving through fairly stationary air.  An object moving through a stationary fluid or gas is equivalent to a stationary object submerged in a fluid or gas flowing with the same speed in the opposite direction in another reference frame.  The picture on the right can be viewed as a fluid flowing past a stationary sphere in laminar flow in one reference frame, or a sphere moving through the fluid in another reference frame.