Mirrors

Images

The purpose of most optical instruments is to produce an images.  Images can be formed by reflection and refraction.

What is an image?

We see objects, because they either emit or reflect light.  We visually identify objects by the pattern of light that they emit or reflect.  We gather some portion of that light on a detector (our eyes).  In interpreting the pattern, we implicitly assume that the light traveled in a straight line from the object to the detector.

• A real image of an object produces the same pattern of light as the object does somewhere in space.  Some portion of the light from the real image reaches our detector along a straight-line path.  The detector cannot distinguish between light coming from the object and light coming from the image.  We interpret the same patterns in the same way.
• A virtual image is the apparent position from which a pattern of light reaches our detector, if we make the assumption that it has traveled from its source to the detector along a straight-line path.  Virtual images are formed when light from an object or from an image is reflected or bend on the way to the detector.

Curved mirrors can produce real and virtual images by reflection.  A flat mirror only produces virtual images.

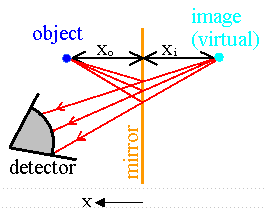Consider a flat mirror. Light rays coming from any point on the object reflect off the mirror before hitting a detector.  For each ray θ_i = θ_r.  The rays reflect in such a way that they seem to come from a point behind the mirror.  For the detector, the apparent position of the object point is behind the mirror.  That position is the image point.  Let x_o denote the perpendicular distance of the object point from the mirror surface, and let x_i denote the perpendicular distance of the image point  from this surface.  If we let distances in front of the mirror be positive and distances behind the mirror be negative, then we have x_o + x_i = 0.

For mirrors, negative image distances are associated with virtual images and positive image distances are associated with real images.
Virtual images appear behind the mirror, real images appear in front of the mirror.

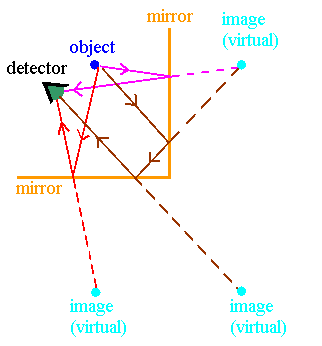Multiple images can be formed by combinations of flat mirrors.  In the picture to the right, light bouncing off one or both of the mirrors can reach the eye along three different paths.  The detector sees three virtual images.

Problem:

Determine the minimum height of a vertical, flat mirror in which a person 5'10'' in height can see his or her full image.

Solution:

• Reasoning:
  There must be a way to reflect rays coming from the foot and rays coming from the head in a way so that they reach the eye. (See image.)  The height of the mirror must be half the height of the person, in this case 2'11''.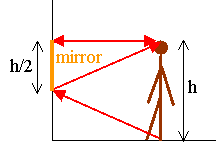
  

Curved Mirrors

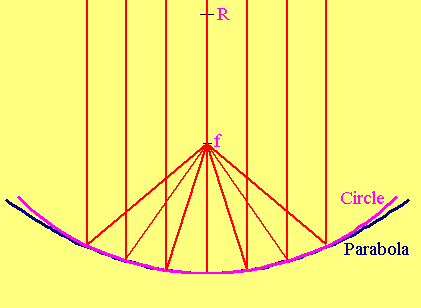Light rays from a distant star are nearly perfectly parallel to each other when they reach Earth.  To produce a bright image of the star we want to gather as much light from the star as possible and bring it together in one spot, called a focus.  A mirror with a parabolic surface can perfectly focus incoming light rays parallel to its axis.  It produces a real image in the focal point of the parabola.  A parabola is the locus of all points, which are equidistant from a line and a point (the focal point).  All light rays from a distant source approaching the parabola parallel to its symmetry axis and reflecting from its surface have the same minimum travel time to the focal point of the parabola.  By Fermat's principle, light will therefore take all these paths, and the rays will come together at the focus.

A concave mirror with a spherical surface focuses light similarly to a parabolic mirror as long as the angle subtended by the spherical mirror section is small.  A spherical mirror has a radius of curvature R and a focal length f = R/2.  The focal length f is the distance between the focus and the surface of the mirror.  The figure on the right compares a parabolic and a concave spherical surface with the same focal length f.  Near the symmetry axis or optical axis the curves are nearly identical.

As long as all light rays stay close to and make small angles with the optical axis, we can write down a simple formula for spherical mirrors relating object and image distances and the radius of curvature and focal length.  This formula is valid in the paraxial approximation.

If an object is placed in front of a spherical mirror at an object distance x_o, then an image is formed at an image distance x_i, where x_o and x_i satisfy the mirror equation,

1/x_o + 1/x_i = 1/f = 2/R.

Sign conventions for the mirror equation:

x_i is positive for a real image in front of the mirror surface, and x_i is negative for a virtual image behind the mirror surface.
x_o and x_i are the perpendicular distances from the center plane of the mirror as shown in the drawing below.

The focal length f and the radius of curvature R = 2f are positive for a concave mirror and negative for a convex mirror.  For a concave mirror the reflecting surface bulges inward, and for a convex mirror the reflecting surface bulges outward.

Ray tracing

Please watch the Youtube video "Ray Diagrams - Mirrors".

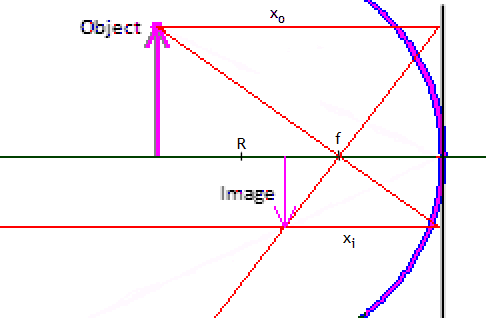
We can determine the positions and sizes of images of points formed by spherical mirrors geometrically by drawing ray diagrams.  Only two incident rays and their reflections must be drawn.  The intersection of the two reflected rays, or, for divergent rays, the intersection of their backward extensions, marks the position of the image of your chosen point on the object.  Choose two or more of the rays listed below.

• Draw the object in front of the mirror surface.
  Draw an incident ray parallel to the optical axis from a point on the object to the mirror line, and a reflected ray from the mirror line through f. 
  (The reflected ray, or an extension of the reflected ray must pass through f.)
• Draw an incident ray through f, and a reflected ray parallel to the optical axis. 
  (The incident ray, or an extension of the incident ray must pass through f.  This can be done if the object is not located a distance f in front of the mirror.)
• Draw a ray through the center of curvature R.  This ray reflects back onto itself.
  (The ray or its extension must pass through R.  This can be done if the object is not located a distance r in front of the mirror.)
• If you have a protractor, draw a line from the object point to the point where optical axis intersects the mirror.  The reflected ray makes the same angle with the optical axis as the incident ray.

In the example diagram a real image is formed by a concave mirror.

The image, in general, has not the same size of the object. 
We define the magnification M as the ratio of the height of the image h_i to the height of the object h_o.  We have from geometry
M = h_i/h_o= -x_i /x_o .

If the magnification is negative, the image is inverted.

Here are some things that always go together for curved mirrors.

• real image <--> inverted image <--> x_i is positive <--> M is negative
• virtual image <--> upright image <--> x_i is negative <--> M is positive

Convex mirrors form only virtual images.
Concave mirrors form real images, if x_o > f and virtual images if x_o < f.  The type of image formed depends on the position of the object.

Please watch this Concave Mirror Demo: Pendulum.

More Demos:

• Concave Mirror Demo
• Convex Mirror Demo

Problem:

A concave mirror has a radius of curvature of 20 cm.  Find the location of the image for object distances
(a) 40 cm,  (b) 20 cm,  (d) 10 cm.
For each case state whether the image is real or virtual, and upright or inverted.  Find the magnification for each case.

Solution:

• Reasoning:
  Use the mirror equation.  1/x_o + 1/x_i = 1/f.   M = -x_i/x_o.
  For a concave mirror f is positive. f = R/2.  For this mirror f = 10 cm.
• Details of the calculation:
  (a) 1/10 - 1/40 = 1/x_i.  3/40 = 1/x_i.  x_i = 13.33 cm.  The image is real.
  M = -x_i/x_o = -1/3.  The image is inverted.
  
  (b) 1/10 - 1/20 = 1/x_i.  1/20 = 1/x_i.  x_i = 20 cm.  The image is real.
  M = -x_i/x_o = -1.  The image is inverted.
  
  (c) 1/10 - 1/10 = 1/x_i.  0 = 1/x_i.  There is no finite image distance.  All rays from the object are parallel after reflection.

Problem:

A object 2 cm in height is placed 3 cm in front of a concave mirror.  If the image is 5 cm in height and virtual, what is the focal length of the mirror?

Solution:

• Reasoning:
  Use the mirror equation.  1/x_o + 1/x_i = 1/f.   M = -x_i/x_o.
• Details of the calculation:
  M = -x_i/x_o = 5/2.  x_o = 3 cm, therefore x_i = -7.5 cm.
  1/x_o + 1/x _i= 1/f.  1/3 - 1/7.5 = 1/f.  f = 5 cm.

Problem:

If an object placed 10 cm in front of a convex mirror produces a virtual image 5 cm behind the mirror, what is the focal length of the mirror?

Solution:

• Reasoning:
  Use the mirror equation.  1/x_o + 1/x_i = 1/f.
• Details of the calculation:
  1/10 - 1/5 = 1/f.  f = -10 cm.

Problem:

A concave mirror forms an inverted image, four times larger than the object.  If the distance between image and object is 1.5 m, find the radius of curvature R of the mirror.

Solution:

• Reasoning:
  Use the mirror equation.  1/x_o + 1/x_i = 1/f.   M = -x_i/x_o.
  An inverted image is a real image. It forms in front of the mirror, the image distance is positive.
• Details of the calculation:
  We have M = -x_i/x_o = -4, x_i = 4x_o.
  1/x_o + 1/(4x_o) = 1/f, f = (4/5)x_o.
  x_o is not given, but the distance between x_i an x_o is given.
  x_i = 4x_o, and both object and image are in front of the mirror.
  Therefore the distance between image and object = 4x_o - x_o = 3x_o = 1.5 m.
  x_o = 0.5 m, f = (4/5)x_o = 0.4 m.
  R = 2f = 0.8 m.

Embedded Question 2

Explore this interactive simulation.

1. Use a concave mirror to produce a real image which is bigger that the object.
2. Use a concave mirror to produce a real image which is smaller that the object.
3. Use a concave mirror to produce a virtual.
4. Use a convex mirror to produce an image.

Discuss these four cases with your fellow students in the discussion forum!
Can you think of situations where spherical mirrors are used to produce the images explored in case 1 - 4.
If you have a shaving or make-up mirror, you have a concave mirror?  Lay it flat on the floor under a lamp or other object that is mounted on the ceiling.
Stand slightly to the side and try to see the image of the lamp or object.
It may take some moving your head around, but do you see the real image of the lamp or object floating above the mirror>

Additional information:  The Physics Classroom: Reflection and the Ray Model of Light