Images formed by refraction at a single interface
Images can be formed by reflection and by refraction.
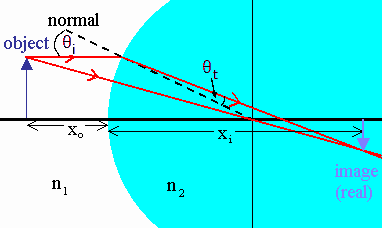
A spherical interface
Assume that we have a boundary between two media with different indices of
refraction n1 and n2, (n1 < n2), and
that the boundary has a radius of curvature R, as shown in the figure below.
The center of curvature is at the origin. Light is refracted at the boundary.
Two rays starting at an object in medium 1 are shown. One ray is incident
on the boundary normally and is not refracted. The other ray is incident
on the boundary at an
angle θi with respect to the normal, and the refracted angle
θt is given by Snell's law, nisinθi = ntsinθt.
A real, inverted image is formed where the two rays intersect in medium 2.
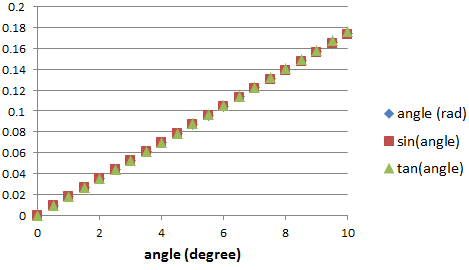 For small angles θ, (θ(rad) << 1) we have sinθ
≈ tanθ ≈ θ.
For small angles θ, (θ(rad) << 1) we have sinθ
≈ tanθ ≈ θ.
(See the graph on the right which
plots θ(rad), sinθ, and tanθ versus θ(deg) for angles from 0
to 10o.)
This is called the small angle approximation. It
simplifies calculations if it is applicable.
Using the
small angle or paraxial approximation we can show that for a spherical interface
n1/xo + n2/xi = (n2 - n1)/R,
if we adopt the following sign conventions.
- The object's position xo is in front of the interface and the object distance is positive.
- The image distance xi is positive if the image position lies behind the interface.
- The image distance xi is negative if the image position lies in front of the interface.
- The radius of curvature R is positive, if the center of curvature lies behind the interface.
- The radius of curvature R is negative, if the center of curvature lies in front of the interface.
The magnification is M = hi/ho = -(n1xi)/(n2xo). If M is negative, the image is inverted.
If medium 1 is air and medium 2 is a transparent material such a water or glass, can you think of situations where we want to produce a real image inside medium 2 of an object located in medium 1? See the problem below!
Problem:
A simple model of the human eye ignores its lens entirely. Much of what
the eye does to light happens at the transparent cornea. Assume that this
outer surface has a radius of curvature of 6 mm, and assume that the eyeball
contains just one fluid of index of refraction n = 1.4. Prove that every
distant object will be imaged on the retina, 21 mm behind the cornea. Describe the image.
 Solution:
Solution:
- Reasoning:
For a single spherical interface we use n1/xo + n2/xi = (n2 - n1)/R.
For distant objects xo is very large and n1/xo is very small.
We can safely ignore this term in the equation n1/xo + n2/xi = (n2 - n1)/R.
We then have n2/xi = (n2 - n1)/R.
R is positive since the center of curvature lies behind the interface. - Details of the calculation:
n2/xi = (n2 - n1)/R yields xi = n2R/(n2 - n1) = (1.4*6 mm)/0.4 = 21 mm.
The image distance is 21 mm.
The image is very small and inverted.
Using the principle of ray reversibility, we can switch out object and image. Let us look at a fish in a water filled spherical bowl. Water has an index of refraction n2 = 1.33, so we cannot produce a real image of the fish in front of the bowl. When looking at the fish from the outside, we will see a upright, enlarged virtual image.
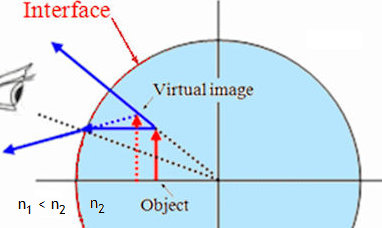
The images below show a frog in a spherical bowl before and after water has been poured into the bowl. The camera is stationary. When the frog is under water, the camera takes a picture of an an upright, enlarged, virtual image of the frog.
 |
Watch as the water is
|
 |
| Frog on empty bowl | Frog under water in bowl |
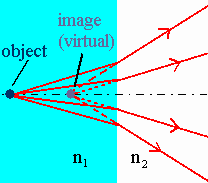
A flat interface
For a
flat interface we have R = infinite and n1/xo + n2/xi = 0.
Let an object be underwater, 10 cm from the water-air interface.
We find xi = -(n2/n1)xo = -(1/1.33)xo. xi
= -7.5
cm.
The magnification is M = 1, it is positive.
The image is a virtual, non-inverted image.
A detector viewing the object from the air side sees the image at the
apparent position closer to the interface.
The images below were taken without moving the camera. A coin is placed in each of two empty bowl. Then water is poured first into the right and then into the left bowl. When the coin is under water, the camera takes a picture of the virtual image of the coin. The coin appears closer to the camera when underwater. (You can verify this yourself.)
| Two empty bowls | Water in the right bowl | Water in both bowls |
Problem:
 A cubical block of ice, 50 cm on a side, is placed on a level floor over
a speck of dust. Find the location of the image of the dust if the index of
refraction of the ice is n = 1.309.
A cubical block of ice, 50 cm on a side, is placed on a level floor over
a speck of dust. Find the location of the image of the dust if the index of
refraction of the ice is n = 1.309.
Solution:
- Reasoning:
For a flat interface we have n1/xo + n2/xi = 0. - Details of the calculation:
xo = 50 cm. xi = -(1/1.309)xo = -38.2 cm.
The apparent position is 38.2 cm below the top surface of the ice.


