Reflection and refraction
Reflection
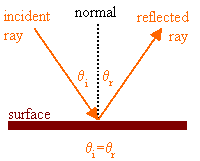 Reflection is the abrupt change in the direction of propagation of a wave
that strikes the boundary between two different media. At least some part of the
incoming wave remains in the same medium. Assume the incoming light ray makes an
angle θi with the normal of a plane
tangent to the boundary. Then the reflected ray makes an angle
θr with this normal and lies in the same
plane as the incident ray and the normal.
Reflection is the abrupt change in the direction of propagation of a wave
that strikes the boundary between two different media. At least some part of the
incoming wave remains in the same medium. Assume the incoming light ray makes an
angle θi with the normal of a plane
tangent to the boundary. Then the reflected ray makes an angle
θr with this normal and lies in the same
plane as the incident ray and the normal.
Law of reflection: θi
= θr.
Note: In geometrical optics, angles are always measured with respect to the normal to the interface.
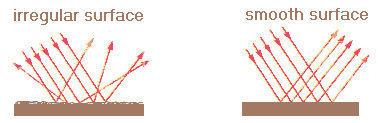 Specular reflection occurs at smooth, plane boundaries. Then the
plane tangent to the boundary is the boundary itself. Reflection at rough,
irregular boundaries is diffuse reflection. The smooth surface of a mirror reflects light specularly, while the rough
surface of a wall reflects light diffusely.
Specular reflection occurs at smooth, plane boundaries. Then the
plane tangent to the boundary is the boundary itself. Reflection at rough,
irregular boundaries is diffuse reflection. The smooth surface of a mirror reflects light specularly, while the rough
surface of a wall reflects light diffusely.
The reflectivity of a surface material is
the fraction of energy of the incoming wave that is reflected by the surface. The
reflectivity of a mirror is close to 1.
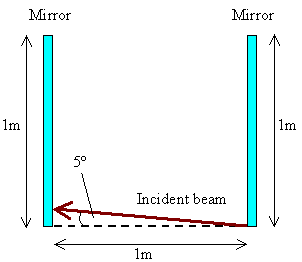 Problem:
Problem:
How many times will the incident beam shown in the figure
to the right be
reflected by each of the parallel mirrors?
Solution:
- Reasoning:
After each path between the mirrors the beam gains a distance d in
height.
- Details of the calculation:
We have d/(1 m) = tan(5o), d = tan(5o) m = 8.75 cm. The
beam must therefore pass 11 times between the mirrors to gain a height
of 1 m, 6 times towards the left and 5 times towards the right.
Refraction
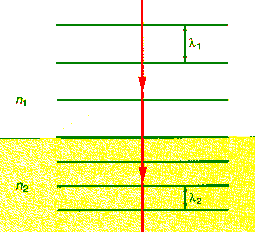 Refraction is the change in direction of propagation of a wave when the wave
passes from one medium into another and changes its speed. Light waves are
refracted when crossing the boundary from one transparent medium into another
because the speed of light is different in different media. Assume that light
waves encounter the plane surface of a piece of glass after traveling initially
through air as shown in the figure to the right.
Refraction is the change in direction of propagation of a wave when the wave
passes from one medium into another and changes its speed. Light waves are
refracted when crossing the boundary from one transparent medium into another
because the speed of light is different in different media. Assume that light
waves encounter the plane surface of a piece of glass after traveling initially
through air as shown in the figure to the right.
What happens to the waves as they pass into the glass and continue to travel
through the glass?
The speed of light in glass or water is less than the speed
of light in a vacuum or air. The speed of light in a given substance is v = c/n,
where n is the index of refraction
of the substance. Typical values for the index of refraction of glass are
between 1.5 and 1.6, so the speed of light in glass is approximately two-thirds
the speed of light in air. The distance between wave fronts will therefore be
shorter in the glass than in air, since the waves travel a smaller distance per
period T.
If f is the frequency of the wave and T = 1/f is
the period, i.e. the time interval between successive crests passing a fixed
point in space, then λ1 = v1T = cT/n1 and λ2
= v2T = cT/n2,
or
λ1/λ2
= n2/n1.
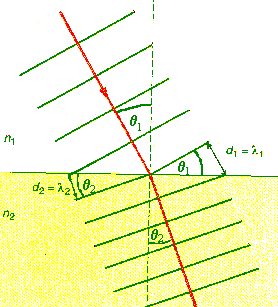 Now
consider wave fronts and their corresponding light rays approaching the surface
at an angle.
Now
consider wave fronts and their corresponding light rays approaching the surface
at an angle.
We can see that the rays will bend as the wave passes from air to glass. The
bending occurs because the wave fronts do not travel as far in one cycle in the
glass as they do in air. As the diagram shows, the wave front halfway into the
glass travels a smaller distance in glass than it does in air, causing it to
bend in the middle. Thus, the ray, which is perpendicular to the wave front, also
bends. The situation is like a marching band marching onto a muddy field at an
angle to the edge of the field. The rows bend as the speed of the marchers is
reduced by the mud.
 The amount of bending of the light depends on the angle of incidence and
on the indices of refraction of glass and air, which determine the change in
speed. From the figure we can see that λ1/λ2
= sinθ1/sinθ2.
The amount of bending of the light depends on the angle of incidence and
on the indices of refraction of glass and air, which determine the change in
speed. From the figure we can see that λ1/λ2
= sinθ1/sinθ2.
But λ1/λ2
= n2/n1. Therefore n2/n1 = sinθ1/sinθ2,
or n1sinθ1 = n2sinθ2.
This is Snell's law, or
the law of refraction.
n1sinθ1 = n2sinθ2.
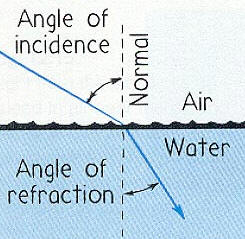
 When light passes from one transparent medium to another, the rays
bend toward the surface normal if the speed of light is smaller in the second medium
than in the first. The rays bend away from this normal if the speed of light
in the second medium is greater than in the first. The picture on the
right shows a
light wave incident on a slab of glass.
When light passes from one transparent medium to another, the rays
bend toward the surface normal if the speed of light is smaller in the second medium
than in the first. The rays bend away from this normal if the speed of light
in the second medium is greater than in the first. The picture on the
right shows a
light wave incident on a slab of glass.
One part of the wave is reflected, and another part is refracted
as it passes into the glass. The rays bend towards the normal. At the second
interface from glass into air the light passing into the air is refracted again.
The rays now bend away from the normal.
Parallel displacement: When a light ray travels from air through a
rectangular block of glass and the angle of incident is not equal to zero, then,
upon reemerging from the glass, the light ray is displaced parallel to its
original path.
Problem:
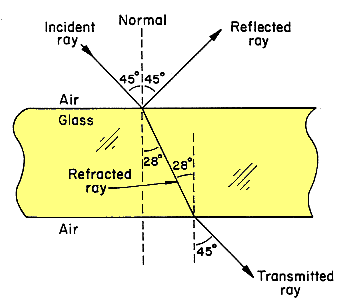 The path of light in air incident on and transmitted through a glass
plate is shown in the figure on the right. The angle of the incident ray to the normal is 45o and equals that of the
reflected ray. The transmitted ray is refracted at an angle of 28o to the
normal and exits the glass at an angle of 45o to the normal, an angle equal
to that of the incident ray. What is the index of refraction of the glass?
The path of light in air incident on and transmitted through a glass
plate is shown in the figure on the right. The angle of the incident ray to the normal is 45o and equals that of the
reflected ray. The transmitted ray is refracted at an angle of 28o to the
normal and exits the glass at an angle of 45o to the normal, an angle equal
to that of the incident ray. What is the index of refraction of the glass?
Solution:
- Reasoning:
We use Snell's law.
nisinθi = ntsinθt
- Details of the calculation:
As the ray
enters from the air into the glass, we have ni = 1,
θi = 45o, and θt
= 28o. We therefore have nt = nisinθ/sinθt
= sin45o/sin28o = 1.5.
Problem:
Assume a light signal travels in a straight line through a medium with index
of refraction of n = 1.55, such as an optical fiber. How long does it take
the signal to travel 20 cm?
Solution:
- Reasoning:
The speed of light in the medium is v = c/n.
- Details of the calculation:
v = d/t. t = d/v =
(0.2 m)* 1.55/(3*108 m/s) = 1.03*10-9 s = 1.03 ns.
At a boundary between two
transparent media, light is partially reflected and partially refracted.
The ratio of the reflected intensity to the incident intensity is called the
reflectance R and the ratio of the transmitted intensity to the incident
intensity is called the transmittance T. Energy conservation requires that
R + T = 1 (if there is no absorption).
Sunlight
Sunlight originates at the outer surface of the sun, in a region called the
photosphere. This region has a temperature of ~5800 oC. The
distribution of wavelengths in sunlight is determined by the temperature of the
photosphere. Not all sunlight is visible. EM waves in the infrared and
ultraviolet part of the EM spectrum are also produced in the photosphere.
Sunlight travels from the Sun to the Earth through empty space with the speed
of light c. When it enters the earth atmosphere it is refracted. The index of
refraction of air near sea level is only 1.0003, so the refraction is barely
noticeable. Air molecules, water molecules and dust also scatter some of the
light (Rayleigh scattering). These
particles scatter shorter-wavelength light more efficiently that longer-wavelength light. Scattering by tiny particles is always most efficient when the
wavelength of the EM wave approximately matches the size of the tiny particle. The dimensions of the molecules and dust particles are much smaller than the
wavelengths of visible light, so blue light with the shortest wavelength
provides the best match. Blue light is scattered more than red light. Most
sunlight travels directly to our eyes, but the scattered light reaches us by a
more complicated path from different directions. We therefore see the brilliant
yellow disk of the sun (direct light) and the fairly uniformly blue sky
(scattered light).
As the sun rises or sets, light must travel a long distance through the
Earth's atmosphere to reach our eyes. Most of the blue light is scattered away
during this passage through the atmosphere and the direct light from the sun
appears red. Extra dust and ash particles from pollution, forest fires, or
volcanic eruptions enhance the Rayleigh scattering and are responsible for
unusually red sunrises and sunsets.
 Clouds and fog are composed of relatively large water droplets, larger than
the wavelengths of visible light. All wavelengths in the visible spectrum are
scattered very efficiently by these large particles, so that very little direct
sunlight reaches our eyes. The scattered light, however, does not have any
particular color, and clouds and fog appear white.
Clouds and fog are composed of relatively large water droplets, larger than
the wavelengths of visible light. All wavelengths in the visible spectrum are
scattered very efficiently by these large particles, so that very little direct
sunlight reaches our eyes. The scattered light, however, does not have any
particular color, and clouds and fog appear white.
Problem:
 Suppose there is a cloud made up of some unknown particles that absorb
rather than scatter visible radiation. What color would this cloud
appear during the day?
Suppose there is a cloud made up of some unknown particles that absorb
rather than scatter visible radiation. What color would this cloud
appear during the day?
Solution:
- Reasoning:
The cloud would appear black, since no visible light would reach
the observer from the direction of the cloud.
Additional information:
The
Physics Classroom: Refraction and the Ray Model of Light Lessons 1 and 2
 Reflection is the abrupt change in the direction of propagation of a wave
that strikes the boundary between two different media. At least some part of the
incoming wave remains in the same medium. Assume the incoming light ray makes an
angle θi with the normal of a plane
tangent to the boundary. Then the reflected ray makes an angle
θr with this normal and lies in the same
plane as the incident ray and the normal.
Reflection is the abrupt change in the direction of propagation of a wave
that strikes the boundary between two different media. At least some part of the
incoming wave remains in the same medium. Assume the incoming light ray makes an
angle θi with the normal of a plane
tangent to the boundary. Then the reflected ray makes an angle
θr with this normal and lies in the same
plane as the incident ray and the normal. Specular reflection occurs at smooth, plane boundaries. Then the
plane tangent to the boundary is the boundary itself. Reflection at rough,
irregular boundaries is diffuse reflection. The smooth surface of a mirror reflects light specularly, while the rough
surface of a wall reflects light diffusely.
Specular reflection occurs at smooth, plane boundaries. Then the
plane tangent to the boundary is the boundary itself. Reflection at rough,
irregular boundaries is diffuse reflection. The smooth surface of a mirror reflects light specularly, while the rough
surface of a wall reflects light diffusely. Problem:
Problem: Refraction is the change in direction of propagation of a wave when the wave
passes from one medium into another and changes its speed. Light waves are
refracted when crossing the boundary from one transparent medium into another
because the speed of light is different in different media. Assume that light
waves encounter the plane surface of a piece of glass after traveling initially
through air as shown in the figure to the right.
Refraction is the change in direction of propagation of a wave when the wave
passes from one medium into another and changes its speed. Light waves are
refracted when crossing the boundary from one transparent medium into another
because the speed of light is different in different media. Assume that light
waves encounter the plane surface of a piece of glass after traveling initially
through air as shown in the figure to the right. Now
consider wave fronts and their corresponding light rays approaching the surface
at an angle.
Now
consider wave fronts and their corresponding light rays approaching the surface
at an angle. The amount of bending of the light depends on the angle of incidence and
on the indices of refraction of glass and air, which determine the change in
speed. From the figure we can see that λ1/λ2
= sinθ1/sinθ2.
The amount of bending of the light depends on the angle of incidence and
on the indices of refraction of glass and air, which determine the change in
speed. From the figure we can see that λ1/λ2
= sinθ1/sinθ2. When light passes from one transparent medium to another, the rays
bend toward the surface normal if the speed of light is smaller in the second medium
than in the first. The rays bend away from this normal if the speed of light
in the second medium is greater than in the first. The picture on the
right shows a
light wave incident on a slab of glass.
When light passes from one transparent medium to another, the rays
bend toward the surface normal if the speed of light is smaller in the second medium
than in the first. The rays bend away from this normal if the speed of light
in the second medium is greater than in the first. The picture on the
right shows a
light wave incident on a slab of glass. The path of light in air incident on and transmitted through a glass
plate is shown in the figure on the right. The angle of the incident ray to the normal is 45o and equals that of the
reflected ray. The transmitted ray is refracted at an angle of 28o to the
normal and exits the glass at an angle of 45o to the normal, an angle equal
to that of the incident ray. What is the index of refraction of the glass?
The path of light in air incident on and transmitted through a glass
plate is shown in the figure on the right. The angle of the incident ray to the normal is 45o and equals that of the
reflected ray. The transmitted ray is refracted at an angle of 28o to the
normal and exits the glass at an angle of 45o to the normal, an angle equal
to that of the incident ray. What is the index of refraction of the glass? Clouds and fog are composed of relatively large water droplets, larger than
the wavelengths of visible light. All wavelengths in the visible spectrum are
scattered very efficiently by these large particles, so that very little direct
sunlight reaches our eyes. The scattered light, however, does not have any
particular color, and clouds and fog appear white.
Clouds and fog are composed of relatively large water droplets, larger than
the wavelengths of visible light. All wavelengths in the visible spectrum are
scattered very efficiently by these large particles, so that very little direct
sunlight reaches our eyes. The scattered light, however, does not have any
particular color, and clouds and fog appear white. Suppose there is a cloud made up of some unknown particles that absorb
rather than scatter visible radiation. What color would this cloud
appear during the day?
Suppose there is a cloud made up of some unknown particles that absorb
rather than scatter visible radiation. What color would this cloud
appear during the day?