PV = Nk_BT is called the ideal gas law.  It is the equation of state, which relates the quantities V, P, and T.  Most real gases at ordinary temperatures and pressures obey the ideal gas law.  The ideal gas law can be rewritten as

PV = nN_Ak_BT = nRT.

Here n is the number of moles of the gaseous substance, N_A is Avogadro's number, N_A = 6.022*10²³ molecules/mol,  and R = N_Ak_B is a constant, called the universal gas constant,  R = 8.31 J/(mol K). 
The number of moles n is given by n = m/M where m is the average mass of the gas particles in the volume,  and M is the molar mass of the gas.

In the 17^th and 18^th century experiment with gases at very low temperature and pressures revealed three relations that are generalized by the ideal gas law.

• For a low-density gas at constant temperature, P is inversely proportional to V.
  Boyle's law:  PV = constant (at constant T).
• For a low-density gas at constant volume the pressure is proportional to the temperature.
  Law of Gay-Lussac:  P = constant * T (at constant V).
• For a low-density gas at constant pressure the volume is proportional to the temperature.
  Charles's Law:  V = constant * T (at constant P).

The ideal gas law holds well for real gases at low densities and pressures, such as atmospheric density and pressure.  If we use T = 0 ^oC = 273 K and P = 1 atm, then we find that one mole of gas occupies a volume of 22.4 liters.  One mole of gas contains N_A gas particles.  For all low density gases, N_A gas particles occupy 22.4 liters at T = 273K and P = 1 atm.

Nothing in the ideal gas law depends on the nature of the gas particles.  The value of PV/T depends only on the number of gas particles and a universal constant. 

Note:  In all gas laws T denote the absolute temperature, measured in Kelvin in SI units.

Problem:

The particle density of atmospheric air at 273.15 K at sea level is 2.687*10²⁵/m³.  Calculate the pressure P.

Solution:

• Reasoning:
  The ideal gas law, PV = Nk_BT, P = (N/V)k_BT = ρ_particlek_BT.
• Details of the calculation:
  P = (2.687*10²⁵/m³)(1.381*10^-23 Pa m³/K)(273.15 K) = 1.01*10⁵ Pa  = 101 kPa.

Problem:

If a helium-filled balloon initially at room temperature is placed in a freezer, will its volume increase, decrease, or remain the same?

Solution:

• Reasoning:
  The ideal gas law states that PV/T is constant.  The pressure in the freezer is atmospheric pressure, the temperature in the freezer is lower that the outside temperature, so the volume of the balloon decreases when it is placed into the freezer. 

External link:  Balloons in Liquid Nitrogen  (Youtube)

Problem:

A tank having a volume of 0.1 m³ contains helium gas at 150 atm.  How many balloons can the tank blow up, if each filled balloon is a sphere 0.3 m in diameter at an absolute pressure of 1.2 atm?

Solution:

• Reasoning:
  At constant temperature P₁V₁ = P₂V₂.  (Boyle's law)
• Details of the calculation:
  P₁ = 150 atm = 1.515*10⁷ Pa.  V₁ = 0.1 m³.
  P₂ = 1.2 atm = 1.212*10⁵ Pa.
  V₂ = P₁V₁/P₂ = 12.5 m³.
  Let n = number of balloons and V_b = the volume of each blown-up balloon.
  V_b = (4π/3)r³ = 1.414*10^-2 m³.
  n = V₂/V_b = 884.  The tank can blow up 884 balloons.

Problem:

The mass of a hot air balloon and its cargo (not including the air inside) is 200 kg.  The air outside is at 10 ^oC and 101 kPa.  The volume of the balloon is 400 m³.  To what temperature must the air in the balloon be heated before the balloon will lift off.  (Air density at 10 ^oC is 1.25 kg/m³.)

Solution:

• Reasoning:
  For the balloon to lift off, the buoyant force B must be greater than its weight. 
  The buoyant force is equal to the weight of the displaced air at 10 ^oC = 283 K. 
  B = (1.25 kg/m³)(400 m³)(9.8 m/s²) = 4900 N.
  The weight of the balloon is 200 kg(9.8 m/s²) + weight of hot air. 
  The hot air therefore must weigh less than 4900 N - 1960 N = 2940 N. 
  Its mass must be less than 2940 N/(9.8 m/s²) = 300 kg. 
  Its density must be less than ρ = 300 kg/(400 m³) = 0.75 kg/m³.
  At constant pressure, the volume of a gas is proportional to the absolute temperature.  (Law of Gay-Lussac)  The pressures on the inside and outside of the inflated balloon are nearly equal.  The pressure on the outside is the constant atmospheric pressure.  The Law of Gay-Lussac therefore applies.
  Since the volume of a gas at constant pressure is proportional to its temperature, its density ρ = m/V is proportional to 1/T. 
  We have ρ₁/ρ₂ = T₂/T₁.  ρ₁T₁/ρ₂ = T₂. 
• Details of the calculation:
  (1.25 kg/m³)(283 K)/(0.75 kg/m³) = 472 K = T₂. 
  The air in the balloon must be heated to more than 472 K = 199 ^oC.

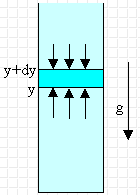The earth atmosphere is a gas in the presence of gravity.  Gravity prevents the atmosphere from escaping.  Near the Earth's surface the acceleration due to gravity is approximately constant (g = 9.8 m/s²).  The atmosphere is a fluid, and the pressure in this fluid is a function of the altitude.  For a liquid, i.e.  an incompressible fluid, we found that P = P₀ + ρgy, where y is the distance below the reference point.  But the atmosphere is a compressible gas.  Let us consider a column of gas containing ρ_particle particles of mass m per unit volume near the Earth's surface.

The pressure times the area (i.e.  the force) at height y must exceed that at height y + dy by the weight of the intervening gas.  We need 
P_y+dyA - P_yA = -mρ_particleVg = -mρ_particlegAdy,  or 
dP = -mρ_particlegdy. 

But from the ideal gas law we know that P = ρ_particlekT, with k being the Boltzmann constant.  We may therefore write
dP = -P(mg/kT)dy, or 
dP/P = -(mg/kT)dy. 

If the temperature T is constant, then this integrates to 
P = P₀e^-mgy/(kT). 

The pressure decreases exponentially with altitude.
Near Earth's surface the temperature T is not constant, it generally decreases with altitude y.  In the standard atmosphere T = T₀ - ay, with a = 0.0065 K/m.  We then have 
dP/P = -mgdy/(k(T₀ - ay)). 

This integrates to 
ln(P/P₀) =( mg/ka)ln(1 - ay/T₀), or 
(P/P₀)^(ka/mg) = (1 - ay/T₀).

Since the Earth's atmosphere consists mostly of nitrogen molecules, we have 
(P/P₀)^0.19 = (1 - (0.0065 (K/m))y/T₀).

T₀ and P₀ are the temperature (in Kelvin) and the pressure at sea level and the altitude y is measured in m.  The pressure, density, and temperature of the atmosphere decrease as the altitude increases.

External link:  Standard Atmosphere Calculator

How can we make a balloon rise?

We have to make its weight smaller than the weight of an equal shaped volume of surrounding air.  The skin of the balloon and the basket certainly are heavier than an equal volume of the surrounding air.  The inside of the skin therefore has to be filled with something appreciably lighter than the surrounding air.  Ideally we would empty it out completely.  But then the pressure inside would be zero.  The air pressure from the outside would collapse the skin.  To keep the skin stretched, the inside and outside pressures on each section of skin must be equal, but the weight of the inside material must be less than that of an equal volume of surrounding air.  The pressure is proportional to the particle density and the temperature, while the weight is proportional to the particle density and the weight of each particle.

P = kρ_particleT,

weight = ρ_particle * volume * weight per particle.

To get the weight down and keep the pressure the same we have two options.

• Option 1:
  We can decrease the weight per particle.  Air is composed of 77% nitrogen, 21% oxygen and 2% other gases by weight.  The density of air at room temperature and atmospheric pressure is approximately 1.3 kg/m³.  If we replace the air with Helium gas at the same temperature, the same particle density will yield the same pressure.  But the mass density of Helium gas at room temperature and atmospheric pressure is only approximately 0.18 kg/m³.  If we make the balloon big enough, the total volume of air displaced by the balloon will weigh more than the balloon itself, and the net force on the balloon will be upward.  Since the density of air decreases with altitude, the weight of the volume of air displaced by the balloon will decrease as the Helium balloon rises.  Eventually it will equal the weight of the balloon and the net force on the balloon will be zero.  As the balloon is rising, it is also acted on by the drag force.  The direction of the drag force is opposite the direction of the balloon's velocity.  Because the drag force the the acceleration of the balloon will quickly decrease to close to zero and the balloon will rise with nearly constant velocity.  You can explore this behavior in an exercise associated with this module.
• Option 2:
  We can increase the temperature of the air in the balloon.  Then we can obtain the same pressure with a smaller particle density.  Again the weight of the balloon decreases and the net force on the balloon is upward.  The hot air balloon will rise.