How do we measure temperature?
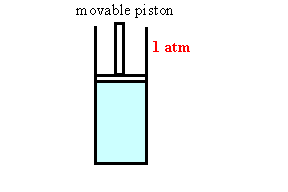 Assume we have a gas in a container with a movable
piston under atmospheric pressure. As we increase the
temperature of the gas it expands, its volume increases. The
piston moves out. As we cool the gas the piston moves in.
The ideal gas law gives us the volume of the gas as a function of
temperature.
Assume we have a gas in a container with a movable
piston under atmospheric pressure. As we increase the
temperature of the gas it expands, its volume increases. The
piston moves out. As we cool the gas the piston moves in.
The ideal gas law gives us the volume of the gas as a function of
temperature.
PV = NkBT, V = (NkB/P)T.
The volume is proportional to the absolute temperature of
the gas. Assume the temperature change from 0 oC to
10oC. We have
(ΔV/V) = (ΔT/T) = 10/273 = 0.037 = 3.7%.
By monitoring the volume of the gas we can monitor its
temperature. We have a gas thermometer.
We could also build a gas thermometer by keeping the volume of the gas
constant and monitoring the pressure.
Problem:
In a constant volume gas thermometer the pressure at 20 oC is 0.98
atm.
(a) What is the pressure at 45o C?
(b) What is the temperature if the pressure is 0.5
atm?
Solution:
- Reasoning:
The ideal gas law, PV/T = constant. Since V is constant, P/T =
constant. P1/T1
= P2/T2. P1T2/T1
=
P2.
- Details of the calculation:
(a)
P2 = (0.98 atm)(318 K/293 K) =1.064 atm.
(b) P2T1/P1
= T2. T2 =
(0.5 atm)(293 K)/(0.98 atm) = 149.5 K.
Solids and liquids also expand as the temperature
increases. For most solids we can define an average coefficient of linear expansion, α. The
change in length Δl of a solid is proportional to its length
l and the change in temperature ΔT. The proportional
constant is α.
Δl = αlΔT.
The average volume expansion coefficient β is defined through
ΔV = βVΔT. We have β = 3α.
Linear expansion coefficients α: (per oC)
| Aluminum |
23 * 10-6 |
| Copper |
17 * 10-6 |
| Glass (ordinary) |
9 * 10-6 |
| Glass (Pyrex) |
3.2 * 10-6 |
| Steel |
11 * 10-6 |
| Invar |
0.7 * 10-6 |
For some applications it is important to choose materials that
have a small coefficient of linear expansion. Temperature
variations can destroy a precision alignment. For other
applications it is important that all materials have similar
coefficients of linear expansion. When different parts of a structure
expand by different amounts, the structure buckles.
Problem:
How much taller does the Eiffel Tower become at the end of a day
when the temperature has increased by 15 oC? Its original
height is 321 m and you can assume it is made of steel.
Solution:
- Reasoning:
Thermal expansion: Δl = αlΔT, α =
coefficient of linear expansion.
- Details of the calculation:
Δl = αlΔT = (11*10-6/oC)*(321
m)*(15 oC) = 5.3*10-2 m = 5.3 cm.
The height of the tower increases by 5.3 cm.
Problem:
A copper telephone wire has essentially no sag
between poles 35 m apart on a winter day when the temperature is -20 oC.
How much longer is the wire on a summer day, when the temperature is 35 oC?
Solution:
- Reasoning:
Thermal expansion: Δl = αlΔT, α =
coefficient of linear expansion.
- Details of the calculation:
Δl = αlΔT. For copper α = 17*10-6
per oC. Δl = (17*10-6)(35 m)55 = 0.0327 m = 3.27
cm.
Problem:
A square hole 8 cm along each side is cut in a
sheet of copper. Calculate the change in the area of the hole if the
temperature of the sheet is increased by 50 K.
Solution:
- Reasoning:
Thermal expansion: Δl = αlΔT, α = linear
expansion coefficient, 2α = area expansion coefficient ,
- Details of the calculation:
ΔA = 2αAΔT. For copper α = 17*10-6 per
oC. ΔA = (34*10-6)(64 cm2)50 = 0.109 cm2.
Problem:
How large an expansion gap should be left between steel railroad rails if
they may reach a maximum temperature 35.0 oC greater than when
they were laid? Their original length is 10.0 m.
Solution:
- Reasoning:
Thermal expansion: Δl = αlΔT, α =
coefficient of linear expansion.
What is the increase in length for each rail?
- Details of the calculation:
Δl = αlΔT = (11*10-6/oC)*(10
m)*(35 oC) = 3.85*10-3 m ~ 4 mm.
If we want to build a thermometer, we want to use a
material with a large coefficient of volume expansion. For
most liquids, the coefficient of volume expansion is on the order of
10-4. For each degree Celsius temperature change,
the volume changes by (ΔV/V) = β = 10-4 = 0.0001 = 0.01%.
If we tried to observe this change by monitoring the height of water
in a glass, we would probably be unsuccessful.
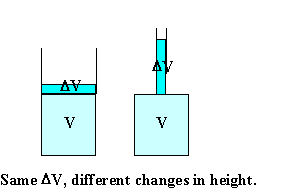 Assume you have 1 liter = 1000 cm3 of liquid with β =
10-4 in a container with bottom area A = 100 cm2.
Assume you have 1 liter = 1000 cm3 of liquid with β =
10-4 in a container with bottom area A = 100 cm2.
The height of the liquid is 1 cm. (Volume = area * height.)
You increase the temperature of the liquid by 20 oC.
ΔV = βVΔT = 10-4 * 1000 cm3 * 20 = 2 cm3.
The change in height is Δh = ΔV/A = 2 cm3/(100 cm2)
= 0.02 cm = 0.2 mm.
If, however, you put a tight lid on the container at a height of
10 cm with a hole connected to a fine capillary, then the liquid
will rise in the capillary to a much greater height. Assume
you connected a tube with a cross sectional area of 1 cm2.
Then Δh = ΔV/A = 2 cm3/(1 cm2) = 2 cm.
You have constructed a usable thermometer.
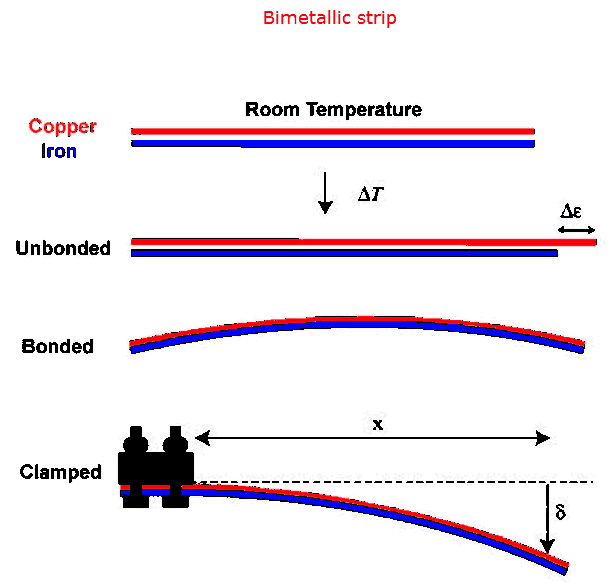
Thermometers can also be constructed from bimetallic
strips. Two strips of metal, one of steel and one of aluminum,
that have the same length at 0 oC, will have different length a 200
oC. Assume the strips are 10 cm long at 0 oC. The
change in length of the steel strip at 200 oC is Δl = αlΔT
= 11*10-6*10 cm*200 = 0.022 cm = 0.22 mm and the change in length of
the aluminum strip at 200 oC is Δl = αlΔT = 23*10-6*10
cm*200 = 0.046 cm = 0.46 mm. If the two strips are bonded together, the
bimetallic strip will buckle or curl. Long bimetallic coils will uncoil
slightly as the temperature rises if the inner strip has the larger α. If
one end is fixed and a pointer is attached to the other end the pointer will
move. The position of the pointer indicates the temperature.
External link: Bimetallic strip demo (video)
Some liquid crystals
change color when their temperature changes. They selectively only reflect
one color of the white light falling onto them. The color that is
reflected back depends on the temperature and can be used as a temperature indicator.
Embedded Question 1
When a cold alcohol thermometer is placed in a hot liquid, the column of
alcohol goes down slightly before going up. Explain why.
Discuss this with your fellow students in the discussion forum!
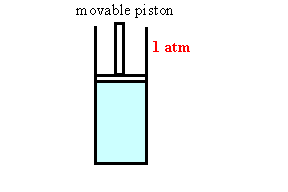 Assume we have a gas in a container with a movable
piston under atmospheric pressure. As we increase the
temperature of the gas it expands, its volume increases. The
piston moves out. As we cool the gas the piston moves in.
The ideal gas law gives us the volume of the gas as a function of
temperature.
Assume we have a gas in a container with a movable
piston under atmospheric pressure. As we increase the
temperature of the gas it expands, its volume increases. The
piston moves out. As we cool the gas the piston moves in.
The ideal gas law gives us the volume of the gas as a function of
temperature. Assume you have 1 liter = 1000 cm3 of liquid with β =
10-4 in a container with bottom area A = 100 cm2.
Assume you have 1 liter = 1000 cm3 of liquid with β =
10-4 in a container with bottom area A = 100 cm2.
