Consider a system in two different conditions, for example 1kg of ice at 0 ^oC, which melts and turns into 1 kg of water at 0 ^oC.  We associate with each condition a quantity called the entropy.  The entropy of any substance is a function of the condition of the substance.  It is a physical property of the substance.  For an ideal gas it is a function of its temperature and volume, and for a solid and liquid it is a function of its temperature and internal structure.  The entropy is independent of the past history of the substance.  The entropy of the 1 kg of water at 0 ^oC is the same if we obtained the water from ice, or if we cooled the water from room temperature down to 0 ^oC.  When a small amount of heat ΔQ is added to a substance at temperature T, without changing its temperature appreciably, the entropy of the substance changes by ΔS = ΔQ/T.  When heat is removed, the entropy decreases, when heat is added the entropy increases.  Entropy has units of Joules per Kelvin.

To calculate the change in entropy of a system for a finite process, when T changes appreciably, we find some reversible path that can take the system (infinitely slowly) from its initial to its final state and evaluate ΔS for that path.  The actual path of the system from the initial to the final state may be very different and not reversible.  But the change in entropy depends only on the initial and final state, not on the path.

ΔS = ∫_i^f dS = ∫_i^f dQ_r/T,

where the subscript r denotes a reversible path.

An ideal frictionless reversible engine removes ΔQ₁ from some substance at T₁, does some work, and delivers ΔQ₂ at to some other substance at T₂, with ΔQ₁/T₁ = ΔQ₂/T₂.  The entropy of the substance at T₁ decreases by ΔS₁ = ΔQ₁/T₁ and the entropy of the substance at T₂ increases by ΔS₂ = ΔQ₂/T₂, i.e.  by the same amount.  There is no net change in entropy, if we consider the entire system.  But a real engine always delivers more heat at T₂ than a reversible engine.  For a real engine ΔS₂ = ΔQ₂/T₂ is always greater than ΔS₁ = ΔQ₁/T₁.  The entropy of the substance at T₁ decreases, but the entropy of the substance at T₂ increases by a larger amount.  The entropy of the whole system increases.

The total entropy of a closed system is always increasing is another way of stating the second law of thermodynamics.

A closed system is a system that does not interact in any way with its surroundings.  In practice there are really no closed systems except, perhaps, the universe as a whole.  Therefore we state the second law in the following way:  The total entropy of the universe is always increasing.  When entropy increases, a certain amount of energy becomes permanently unavailable to do useful work.

Are the laws of physics reversible?

Evidently not!  Where does this irreversibility come from?  If you videotape a sequence of events, and you run the tape backwards, it usually does not take a very long time before everybody notices that something is wrong.  But when you look on a microscopic scale at any particular interaction, such as a collision between two small particles, you find that no interaction violates Newton's laws.  On a microscopic scale each interaction is reversible.  Where then does the large-scale irreversibility come from?

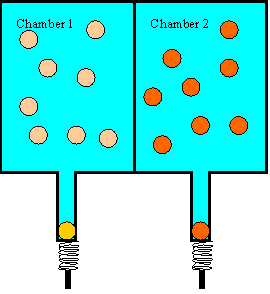Let us look at a simple example of an irreversible process that is completely composed of reversible events.  Consider two chambers, separated by a dividing wall.  Assume we shoot 25 balls into chamber 1, each with 5 J kinetic energy.  The balls will bounce around in the chamber and hit the wall and each other.  If the walls of the chamber are perfectly hard and the coefficient of restitution of the balls is 1, then the average kinetic energy of the balls in chamber 1 will stay 5 J, even so some balls will gain and some will lose energy in the collisions.  Assume we shoot 25 balls into chamber 2, each with 15 J of kinetic energy.  The average kinetic energy of these balls will stay 15 J.  So as long as chamber 1 and chamber 2 are separated by a dividing wall, the balls on one side will be "hot" and the balls on the other side will be "cool".  If we cut a hole into the dividing wall, big enough for a ball to pass through, and wait long enough, the average kinetic energy of the balls on either side of the wall will be approximately 10 J.  There will be 'hot" balls, with energies above 10 J, and "cool" balls, with energies below 10 J, on either side of the wall.

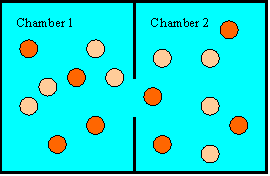While Newton's laws do not forbid all the hot balls to gather on one side and all the cool ones on the other side, the probability that this will happen is practically zero.  There are a very large number of ways to distribute the energy among all the balls.  Any one specific way is equally likely or unlikely.  It is just as unlikely for each ball to have exactly 10 J of kinetic energy than for one ball to have 500 J and all the others to have 0 J.  But there are many more specific ways of distributing the energy so that the average energy is approximately equal on both sides than there are of distributing the energy so that the average kinetic energy is three times as high on side 2 as it is on side 1.  There are many more ways of having a disorderly arrangement than of having an orderly arrangement.

Irreversibility is a probabilistic notion.  Events that do not violate the laws of classical physics nevertheless do not occur because they are just too improbable.

Disorder is more likely than order.  But how do we quantify disorder?

The macrostate of a system is its state as viewed at a macroscopic level.  For instance, to describe the macrostate of an ideal gas in a cylinder, we could specify the number of gas molecules N in the cylinder, the total volume V of the cylinder, and total internal energy U of the gas molecules.  As long as the gas is in internal thermal equilibrium, these three parameters suffice to determine its macrostate.  Other thermodynamic variables, such as the temperature T and the pressure P of the gas, can then be calculated using the ideal gas law PV = NkT and the relation U = (3/2)Nk_BT, where k_B is the Boltzmann constant.  In general, the macrostate of a system is characterized by the numbers and types of particles in the system and by internal parameters, such as mass, charge, and spin, by external physical constraints on the system such as volume, electric fields, and magnetic fields, and by conservation laws, such as energy conservation.

The microstate of a system is its state as viewed at the molecular level.  To describe the microstate of the gas in the cylinder in classical mechanics, we have to specify the exact position and velocity of each individual molecule.  If we know a system's microstate, we also know its macrostate.  On the other hand, knowing a system's macrostate does not imply knowledge of its microstate.

The number of microstates that are consistent with a given macrostate is called the multiplicity Ω of that macrostate.  The multiplicity is the number of accessible microstates, limited only by the constraints that determine the macrostate, i.e. it is the number of ways the insides of a system can be arranged so that from the outside things looks the same.  For our gas in the cylinder, the multiplicity is a function of the three macroscopic variables N, V, and U.  For most macrostates the multiplicity is a very large number, since there are an enormous number of different ways to distribute a given amount of energy among the system's N molecules and to distribute the N molecules throughout the volume V.

The fundamental assumption of statistical mechanics is that an isolated system in equilibrium in a given macrostate is equally likely to be in any of its accessible microstates.

This means that the probability of finding the system in any given microstate is 1/Ω, since there are Ω microstates, all equally probable.  An isolated system is a system of fixed composition, fixed external parameters and fixed total energy.  Equilibrium is the state in which the macroscopic properties are independent of time.

The amount of disorder or the multiplicity Ω is the number of ways the insides of a system can be arranged so that from the outside things looks the same.  It turns out that the logarithm of that number of ways is proportional the entropy S.

S = k_B lnΩ, where k_B is the Boltzmann constant.

We can define the entropy as the logarithm of the disorder times a constant of proportionality.  When we change the entropy of a substance by an amount ΔS = ΔQ/T, we change the disorder of the substance.  Entropy always increases, because a high amount of disorder is, by definition, is more likely than a low amount of disorder.  With our definition of disorder as the multiplicity of the macrostate, every condition of a system has a well-defined disorder.  If this disorder is small, then in common, everyday language, we say that the system is ordered.

We have two ways of figuring out if the entropy of a substance changes.  Both ways will lead to the same answer.  Sometimes it is easier to get the answer by considering the heat transfer to or from the substance.  Sometimes it is hard to follow the heat, but it is easy to decide if the disorder increases or decreases.

Assume that during an irreversible process the entropy of a system increases by ΔS.  Then an amount of energy in the system, E = T_minΔS, is no longer available for useful work.  Here T_min is the lowest temperature available to the system.  Entropy is measure of energy quality.  Given two systems with identical energy content, the one with the lower entropy contains the higher quality energy and can do more useful work.

Here are some situations in which entropy increases:

• The entropy increases whenever heat flows from a hot object to a cold object.  It increases when ice melts, water is heated, water boils, water evaporates.
• The entropy increases when a gas flows from a container under high pressure into a region of lower pressure.  It increases when you spray something out of an aerosol can or you let air out of a tire.
• The entropy increases whenever ordered energy is converted into disordered energy.  Kinetic friction and drag always increase entropy.

When water freezes its entropy decreases.  This does not violate the second law of thermodynamics.  The second law does not say that entropy can never decrease anywhere.  It just says that the total entropy of the universe can never decrease.  Entropy can decrease somewhere, provided it increases somewhere else by at least as much.  The entropy of a system decreases only when it interacts with some other system whose entropy increases in the process.  That is the law.

Problem:

An ice tray contains 500 g of water.  Calculate the change in entropy of the water as it freezes completely and slowly at 0 ^oC. 

Solution:

• Reasoning:
  The water freezes at 0 ^oC = 273 K.  ΔS = ΔQ/T
  ΔQ = -mL, m = mass of water, L = latent heat of fusion = 333000 J/kg. 
• Details of the calculation:
  ΔS = -(0.5 kg)(333000J /kg)/273 K = -610 J/K.

Problem:

If you toss two dice, what is the total number of ways that you can obtain
(a) a 12 and
(b) a 7?

Solution:

• Reasoning:
  (a)  There is only one way to obtain a 12.  Both dice must show a 6.
  (b)  There are six ways to obtain a 7.  If you label the dice by A and B, then there are six possible numbers you can throw with dice A, 1-6.  Each of these numbers has exactly one corresponding number that you must throw with dice B, 6-1, to obtain  7.

Problem:

The surface of the Sun is approximately at 5700 K, and the temperature of the Earth's surface is approximately 290 K.  What entropy changes occur when 1000 J of thermal energy is transferred from the Sun to the Earth?

Solution:

• Reasoning:
  During the process the temperatures of the sun and the earth do not change appreciably.
  The change in the entropy of the sun is therefore ΔS = -1000 J/5700 K = -0,175 J/K. 
  The change in the entropy of the earth is ΔS = 1000J/290 K = 3.448 J/K. 
  The entropy of the sun-earth system increases by 3.27 J/K.

Question:

Consider the following idea:  A ship pumps in warm seawater.  It extracts heat from that water.  It concentrates the extracted heat in its boiler and uses it to power its engine.  It pumps the cooled seawater back into the ocean. 

• Does this process violate the first law of thermodynamics?
• Does this process violate the second law of thermodynamics?

Question:

Water on the top of the Gulf of Mexico is much warmer than water on the bottom.  A ship heats some gas with the warm water from the top and causes it to expand.  It then cools the gas with the water from the bottom and causes it to contract.  The alternate expansion and contraction drives a piston back and forth and powers an engine. 

• Does this process violate the first law of thermodynamics?
• Does this process violate the second law of thermodynamics?

External link:  Ocean thermal energy conversion

Entropy and life

The entropy of isolated systems cannot decrease.  However, when a system is not isolated, but is in contact with its surrounding, then the entropy of this open system may decrease, with a necessary compensating increase in the entropy of the surroundings.

Living systems are characterized by their energy content and by the amount of energy flowing through the system.  Living systems are non-equilibrium systems.  Energy flows from a source through the living system into to a sink.  The living system may be well ordered since it is not an isolated system.

Energy enters into the biosphere as radiation from the sun.  It is stored as chemical energy.  Biological cycles involve a series of biochemical reactions which are accompanied by the production of thermal energy.  Heat flows into the immediate surroundings and finally as radiation into outer space.  Three rules govern every change. 

• The number of atoms is conserved.
• Energy is conserved
• Entropy increases.

A living system is an improbable non-equilibrium state.  A state in thermodynamic equilibrium is a very probable state, but it represents a dead system.  To keep a system alive, it is necessary to constantly do work to move the living system back into the improbable state it is drifting out of.  For this to be possible, the system must be connected to a source and a sink.  The entropy of the source decreases, but the entropy of the sink increases by a larger amount.  The living organism can only exist if the entropy of the rest of the universe is increasing.