Refrigerators, air conditioners, and heat pumps

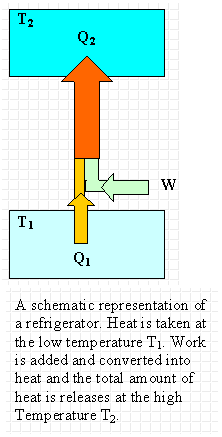imageHeat cannot, of itself, flow from a cold to a hot object is one way of stating the second law of thermodynamics.  If it could, then heat dumped at Tlow could just flow back to the reservoir at Thigh and the net effect would be an amount of heat ΔQ = Qhigh - Qlow taken at a Thigh and converted into work with no other changes in the system.

Assume you want to take heat from a place at Tlow and dump it at a place with a higher temperature Thigh.  You want to build a refrigerator or an air conditioner.  For such a device we define the coefficient of performance COP as the ratio of the amount of heat removed at the lower temperature to the work put into the system (i.e.  the engine).

COP = Qlow/(-W) = Qlow/(Qhigh - Qlow).

The best possible coefficient of performance is

COPmax =  Qlow/(Qhigh - Qlow)max  = Qlow/(Qlow(Thigh/Tlow) - Qlow) = Tlow/(Thigh - Tlow),

if we have a reversible engine moving the heat.  For a real engine Qhigh is bigger than QlowThigh/Tlow, and the coefficient of performance is smaller.

For a refrigerator keeping an inside temperature of 4 oC = 277 K operating in a room at 22 oC = 299 K the best possible coefficient of performance is COPmax = 277/(299 - 277) = 12.6.  The best possible ratio of the amount of heat removed to the work done is 12.6.  Heat cannot flow from inside an ordinary refrigerator into the warmer room unless we plug in the electric motor that does work on the refrigerant.

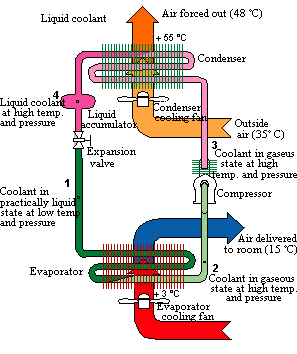imageAn air conditioner is a refrigerator whose inside is the room to be cooled (Troom = Tlow) and whose outside is the great outdoors (Toutside = Thigh).  An air conditioner uses a material called a "working fluid" to transfer heat from inside of a room to the great outdoors.  The working fluid is a material which transforms easily from a gas to a liquid and vice versa over a wide range of temperatures and pressures.  This working fluid moves through the air conditioner's three main components, the compressor, the condenser, and the evaporator in a continuous cycle.

  1. The working fluid enters the evaporator inside the room as a low-pressure liquid at approximately outside air temperature.
  2. The evaporator is typically a snake-like pipe.  The fluid immediately begins to evaporate and expands into a gas.  In doing so, it uses its thermal energy to separate its molecules from one another and it becomes very cold.  Heat flows from the room into this cold gas.  The working fluid leaves the evaporator as a low-pressure gas a little below room temperature and heads off toward the compressor.
  3. It enters the compressor as a low-pressure gas roughly at room temperature.  The compressor squeezes the molecules of that gas closer together, increasing the gas's density and pressure.  Since squeezing a gas involves physical work, the compressor transfers energy to the working fluid and that fluid becomes hotter.  The working fluid leaves the compressor as a high-pressure gas well above outside air temperature.
  4. The working fluid then enters the condenser on the outside, which is typically a snake-like pipe.  Since the fluid is hotter than the surrounding air, heat flows out of the fluid and into the air.  The fluid then begins to condense into a liquid and it gives up additional thermal energy as it condenses.  This additional thermal energy also flows as heat into the outside air.  The working fluid leaves the condenser as a high-pressure liquid at roughly outside air temperature.  It then flows through a narrowing in the pipe into the evaporator.  When the fluid goes through the narrowing in the pipe, it's pressure drops and it enters the evaporator as a low-pressure liquid.  The cycle repeats.

Overall, heat is been extracted from the room and delivered to the outside air.  The compressor consumes electric energy during this process and that energy also becomes thermal energy in the outside air.  The maximum coefficient of such an air conditioner is COPmax = Troom/(Toutside - Troom).  Refrigerators and heat pumps work on the same principle.

A heat pump is a refrigerator whose inside is the great outdoors and whose outside is the room to be heated.  The coefficient of performance for a heat pump is the ratio of the energy delivered at the higher temperature to the work put into the system, COP = Qhigh/(Qhigh - Qlow).  The best possible coefficient of performance is

COPmax(heat pump) = (Qhigh/(Qhigh - Qlow))max
= Thigh/(Thigh - Tlow) = Troom/(Troom - Toutside)

If the outside temperature is 41 oF = 5oC = 278 K and room temperature is 77oF = 25oC = 298K then COPmax = 298/(298 - 278) = 14.9.  However, if the outside temperature drops to 14 oF = -10 oC = 263 K then Emax = 298/(298 - 263) = 8.5.

Note: The coefficient of performance for a refrigerator/air conditioner and the coefficient of performance of a heat pump are defined differently.  We are always interested in how much work we have to do or how much useful energy we have to invest to accomplish something.  For a refrigerator or air conditioner we are interested in how efficiently heat is removed from the colder inside for a given amount of work done.  For a heat pump we are interested in how efficiently heat is delivered to the hotter inside for a given amount of work done.  The coefficient of performance gives us those ratios.

External link:  The refrigeration cycle (Youtube)

Problem:

What is the coefficient of performance of a refrigerator that operates with Carnot efficiency between temperatures of -3 oC and 27 oC?

Solution:

Problem:

A refrigerator has a coefficient of performance equal to 5.  If the refrigerator absorbs 120 J of thermal energy from a cold reservoir in each cycle, find
(a) the work done in each cycle and
(b) the thermal energy expelled to the hot reservoir. 

Solution:

Embedded Question 2

The energy output of a heat pump is greater than the energy used to operate the pump.  Why doesn't this statement violate the first law of thermodynamics?

Discuss this with your fellow students in the discussion forum!