One of the earliest scientists to be intrigued by heat engines was a French engineer named Sadi Carnot (1796-1832). A heat engine uses heat transfer to do work in a cyclical process. After each cycle the engine returns to its original state and is ready to repeat the conversion process (disordered --> ordered energy) again.
Carnot assumed that an ideal engine, converting the maximum amount of thermal energy into ordered energy, would be a frictionless engine. It would also be a reversible engine. By itself, heat always flows from an object of higher temperature to an object with lower temperature. A reversible engine is an engine in which the heat transfer can change direction, if the temperature of one of the objects is changed by a tiny (infinitesimal) amount. When a reversible engine causes heat to flow into a system, it flows as the result of infinitesimally small temperature differences, or because there is an infinitesimal amount of work done on the system. If such a process could be actually realized, it would be characterized by a continuous state of equilibrium (i.e. no pressure or temperature differentials) and would occur at a rate so slow as to require an infinite time. The momentum of any component of a reversible engine never changes abruptly in an inelastic collision, since this would result in an irreversible, sudden increase of disordered energy of that component. A real engine always involves at least a small amount of irreversibility. Heat will not flow without a temperature differential and friction cannot be entirely eliminated.
Carnot showed that if an ideal reversible engine, called a Carnot engine, picks up the amount of heat Q1 from a reservoir at temperature T1, converts some of it into useful work, and delivers the amount of heat Q2 to a reservoir at temperature T2, then Q1/T1 = Q2/T2. Here T is the absolute temperature, measured in Kelvin and a heat reservoir is a system, such as a lake, that is so large that its temperature does not change when the heat involved in the process considered flows into or out of the reservoir. To convert heat into work, you need at least two places with different temperatures. If you take in Q1 at temperature T1 you must dump at least Q2 at temperature T2.
Carnot postulated that heat cannot be taken in at a certain temperature with no other change in the system and converted into work. This is one way of stating the second law of thermodynamics.
An example of an idealized, frictionless engine in which all the processes are reversible is an ideal gas in a cylinder equipped with a frictionless piston. The cylinder alternates in making contact with one of two heat reservoirs at temperatures T1 and T2 respectively, with T1 higher than T2.
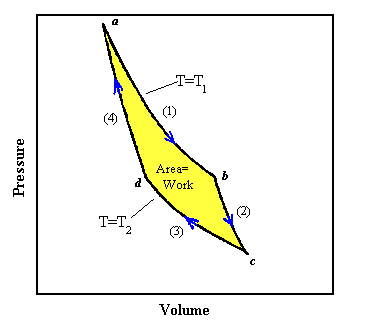
(1) We start at point a in the PV diagram. Let us put the cylinder in contact with the reservoir at T1 and heat the gas and at the same time expand it following the curve marked (1). To make the process reversible we pull the piston out very slowly as heat flows into the gas and we make sure that the temperature of the gas stays nearly equal to T1. If we would push the piston back in slowly, then the temperature would only be infinitesimally higher than T1 and the heat would flow back from the gas into the reservoir. An isothermal expansion, when done slowly enough, can be a reversible process. The curve marked (1) from point a to point b tells us how the pressure and volume change if the temperature is kept fixed at the value T1. For an ideal gas this curve is given by PV = NkT1. As the volume increases, the pressure drops. Once we reach point b in the diagram an amount of heat Q1 has been transferred from the reservoir into the gas. Since the expansion is isothermal, the temperature of the gas has not changed, ΔU = 0 and ΔQ1 = ΔW.
ΔQ1 = ΔW = ∫ab PdV = ∫ab (NkBT1/V) dV = NkBT1 ln(Vb/Va).
ΔQ1 = Q1 is positive, heat flows into the gas in the
cylinder.
(2) Let us take the cylinder away from the reservoir at point b and continue a slow,
reversible expansion without permitting heat to enter the cylinder. The expansion now is
adiabatic. As the gas expands the temperature falls, since there is no heat entering the cylinder. We
let the gas expand, following the curve marked (2), until the temperature falls to T2
at the point marked c. The adiabatic curve has a more negative slope than the
isothermal curve. For the adiabatic expansion of an ideal gas made from point particles,
we have ΔU = -ΔW since ΔQ = 0. Therefore
dU = -dW = -PdV.
But we also have
U = N½m<v2>,
since the internal energy is the random kinetic energy of the gas atoms. Using, from the kinetic theory, PV = (2/3)N½m<v2> we have
U = (3/2)PV.
Then, from calculus, we have
dU = (3/2)(PdV + VdP).
Equating our two expressions for dU we have
-PdV = (3/2)(PdV + VdP),
(-5/2)PdV = (3/2)VdP,
dP/P + (5/3)dV/V = 0.
We can integrate to obtain lnP + (5/3)lnV = lnC, where lnC is the constant of integration. This yields
PV5/3 = C = constant
for an adiabatic expansion of an ideal gas. Since PV = NkT we can write PV5/3 = NkTV2/3 = C, or TV2/3 = constant. Therefore
T1Vb2/3 = T2Vc2/3 or Vb/Vc = (T2/T1)-2/3.
(3) When the gas has reached the temperature T2 we put it in contact with the reservoir at T2. Now we slowly compress the gas isothermally while it is in contact with the reservoir at T2, following the curve marked (3). The temperature of the gas does not rise and an amount of heat ΔQ2 flows from the cylinder into the reservoir at the temperature T2. For the isothermal process we have
ΔQ2 = ΔW = ∫cd PdV = ∫cd (NkBT2/V) dV = NkBT2 ln(Vd/Vc).
ΔQ2 = -Q2 is negative, heat is removed from the gas in
the cylinder.
(4) At the point d we remove the cylinder from the reservoir at T2 and
compress it still further, without letting any heat flow out. During this
adiabatic process the temperature rises, and the pressure follows the curve marked (4). If we carry
out each step properly, we can return to the point a at temperature T1
where we started, and repeat the cycle. For the adiabatic process from point d to point a we have
T2Vd2/3 = T1Va2/3 or Va/Vd = (T2/T1)-2/3.
Therefore
Va/Vd = Vb/Vc, Vb/Va = Vc/Vd, and ln(Vb/Va)= ln(Vc/Vd) = -ln(Vd/Vc).
In going from point a to point c, the gas expands and does work. In going from point c back to point a work is done on the gas. The work done is always the area under the curve in the PV diagram. The net amount of work done by the gas is the yellow area of the figure. Because everything we have done is reversible, we could also have gone backwards instead of forwards through the cycle. Then the area under the curve would represent the net amount of work done on the gas.
During one cycle we have put an amount of heat Q1 into the gas at temperature T1 and have removed an amount of heat Q2 at temperature T2. From the above equations we see that
Q1/Q2 = (T1 ln(Vb/Va))/(T2 ln(Vd/Vc))
= T1/T2, or
Q1/T1
= Q2/T2.
We have shown that if our ideal reversible engine picks up the amount of heat Q1 from a reservoir at temperature T1 and delivers the amount of heat Q2 to a reservoir at temperature T2, then Q1/T1 = Q2/T2. The work done by the engine on its surroundings is W = Q1 - Q2 = Q1 (1 - T2 / T1).
Let us now assume that we have another engine which takes Q1 at T1, does work W', and delivers some heat at T2. If W' were greater than the work W done by our reversible engine, then we could use W to run our reversible engine backwards and put Q1 back into the reservoir at T1. Then all that we would have effectively done by running both engines is to take heat out of the reservoir at T2 and completely converted it into the useful work W' - W. But according to the second law of thermodynamics it is impossible to obtain useful work from a reservoir at a single temperature with no other changes. Heat cannot be taken in at a certain temperature with no other change in the system and converted into work. Therefore no engine which absorbs a given amount of heat from a higher temperature T1 and delivers it at the lower temperature T2 can do more work than a reversible engine operating under the same temperature conditions. If our second engine is also reversible, then W' must be equal to W, or we could reverse the above argument. If both engines are reversible they must both do the same amount of work, and Q1/T1 = Q2/T2 for both engines. If an engine is reversible, it makes no difference how it is designed. The amount of work it does when it absorbs a given amount of heat at temperature T1 and delivers heat at some other temperature T2 does not depend on the design of the engine. It is a property of the world, not a property of a particular engine.
The useful work done by any heat engine which absorb heat at temperature T1
and deliver heat at temperature T2 is
W = Q1 - Q2
(energy conservation). W is positive if T1 is greater than T2.
All reversible heat engines which absorb heat at temperature T1
and deliver heat at temperature T2 do the same amount of
useful work,
Wmax = Q1 - Q2 = Q1 - Q1 T2 / T1 = Q1 (1 - T2 / T1).
Any real engine delivers more heat Q2 at the reservoir at T2 than a reversible one and therefore does less useful work.
The maximum amount of work you can therefore get out of a heat engine is the amount you get from an ideal, reversible engine.
The efficiency of a heat engine is the ratio of the work obtained to the heat energy put in at the high temperature, e = W/Qhigh. The maximum possible efficiency emax of such an engine is
emax = Wmax/Qhigh = (1 - Tlow/Thigh) = (Thigh - Tlow)/Thigh.
Assume you have a reservoir of hot water at temperature T1. Can you take an amount of heat Q1 out of this reservoir and convert it into work? No! You can convert a fraction of the heat into work if you have a place at a lower temperature T2 where you can dump some of the heat. An engine that does work by removing heat from a reservoir at a single temperature cannot exist.
Heat cannot be taken in at a certain temperature with no other change in the system and converted into work. This is one way of stating the second law of thermodynamics.
Heat cannot, of itself, flow from a cold to a hot object is another way of stating the second law of thermodynamics.
If it could, then heat dumped at T2 could just flow back to the reservoir at T1 and the net effect would be an amount of heat ΔQ = Q1 - Q2 taken at a T1 and converted into heat with no other changes in the system.
A certain gasoline engine has an efficiency of 30.0%. What would the
hot reservoir temperature be for a Carnot engine having that efficiency, if it
operates with a cold reservoir temperature of 200 oC?
Solution:
An inventor is marketing a device and claims that it takes 25 kJ of heat at
600 K, transfers heat to the environment at 300 K, and does 12 kJ of work.
Should you invest in this device?
Solution:
Note:
Disordered energy cannot be completely converted back to ordered energy.
The maximum efficiency of a heat engine converting thermal to ordered energy is
100%*(Thigh - Tlow)/Thigh.
Here Thigh and Tlow are the highest and lowest temperature
accessible to the engine.
Ordered energy, on the other hand, can be completely converted into other forms of energy. The maximum efficiency of an engine using ordered energy is 100%.