 The number of field lines passing through a geometrical surface of given area
A depends on three factors.
The number of field lines passing through a geometrical surface of given area
A depends on three factors.The electric field is a vector field. It is a quantity with magnitude and direction defined at every point in space. Another example of a vector field that is easier to visualize is the velocity of water in a stream. The flux of a vector field through a surface area is the amount of whatever the field represents passing through the area. The total flux depends on strength of the field, the size of the surface area it passes through, and on how the area is oriented with respect to the field. You can think of flux as the amount of something crossing a surface. The surface is a two dimensional (real or imagined) boundary. It can be open or closed. An open surface could be a the area of a door, the area of a sheet of paper, the area of a bowl, etc. A closed surface could be the surface are of a sphere or a cube, etc. Flux is measure at a single point in time. Flux is the total amount of something crossing the surface, it is not something per unit area, etc.
Field lines help us to visualize the electric field. The density of the field lines is proportional to the strength of the field.
 The number of field lines passing through a geometrical surface of given area
A depends on three factors.
The number of field lines passing through a geometrical surface of given area
A depends on three factors.
The number of field lines passing through an area A is proportional
to the flux through that area.
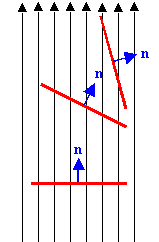
The diagram on the right shows a locally uniform electric field
E. The
lines are parallel and have constant density. The same surface is inserted
in three different orientations. The maximum number of field lines is
intercepted when unit vector normal to the surface, n, is parallel to the
field E, while no field lines pass through the surface when
n is
perpendicular to the field. In general, the number of field lines passing
through an area A is directly proportional to A*cosθ, where θ is the angle
between the field direction and the unit vector n normal to the surface.
This leads to the definition of the electric flux.
ΔΦE = E ΔA cosθ.
ΔΦE is the electric flux
through some small area ΔA, whose normal make an angle θ with the direction of
the electric field. E is the magnitude of the electric field. The SI unit of flux is Nm2/C.
To visualize electric flux in 3D, explore the demonstration below.
Flux of a vector field through an area
E is a vector quantity. It is useful also to represent the area A by a
vector A. The length of this vector is the size of the area, while its
orientation is perpendicular to the area. It is in the direction of the normal
n. We have A = An. The normal to the surface can point into
two different directions. For a closed surface, by convention, the
normal points outward. With our definition of A we can write the flux as the dot product
of E and ΔA.
ΔΦE =
E∙ΔA = En*ΔA = E ΔA cosθ.
ΔΦE is the flux through a small are ΔA, which may be part of a
larger area A. The total electric flux ΦE through A can be evaluated
by summing the differential flux over the all elements of surface A,
ΦE= ∑ΔA -> 0 Eperpendicular
ΔA = ∑ΔA -> 0 E∙ΔA = ∫E∙dA
= ∫EndA,
 The flux through a given surface can be positive or negative, since the
cosine can be positive or negative. The flux through a closed surface is
positive if there is a net outward flow, and negative if there is a net
inward flow. We have a net outward flux if there is a source
inside the closed surface and a net inward flux if there is a sink
inside the closed surface.
The flux through a given surface can be positive or negative, since the
cosine can be positive or negative. The flux through a closed surface is
positive if there is a net outward flow, and negative if there is a net
inward flow. We have a net outward flux if there is a source
inside the closed surface and a net inward flux if there is a sink
inside the closed surface.
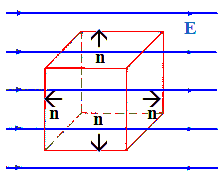
Consider the electrical flux passing through a cubical surface with two of its faces perpendicular to a uniform electrical field. The flux passing through the top, bottom, front, and back sides of the cube is zero since these sides are parallel to the field lines and thus do not intercept any of them. The normal vector n is perpendicular to the field for these sides and cosθ is zero. As drawn, the field lines are parallel to the normal vector n for the right side, so the flux through this side is ΦE = EA. The field lines are anti-parallel to the normal vector n for the left side, so the flux through this side is ΦE = -EA. The total flux through the surface of the cube is the sum of the fluxes through all sides, and it is zero.
The flux of a vector field through a closed surface is always zero if there is no source or sink of the vector field in the volume enclosed by the surface. The sources and sinks for the electric field are charges.
The flux of a electric field through a closed surface is always zero if there is no net charge in the volume enclosed by the surface.
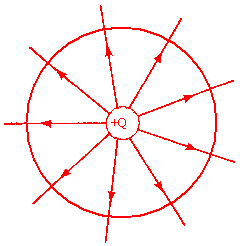 Let us calculate the flux passing through a spherical surface that surrounds a point
charge q at the center of the sphere.
Let us calculate the flux passing through a spherical surface that surrounds a point
charge q at the center of the sphere.
First let us consider the field lines. The field lines radiate outward from the charge. The density of field lines reflects the magnitude of the electrical field at any point. The magnitude of the field and the density of the field lines decrease proportional to the inverse square of the distance r from the charge. The area of the spherical surface increases proportional r2. The total number of field lines passing through the spherical surface, which is perpendicular to the direction of the field at any point, is the product of their density and the area of the surface. It is therefore independent of the size of the sphere. The number of field lines depends only on the magnitude of the charge at the center of the sphere.
Because the flux is proportional to the number of field lines passing through the area, we expect the flux to be proportional to the charge inside the surface. The field of the point charge at the center is radial, pointing towards or away from the point charge. It is everywhere normal to the surface area of the sphere. Its magnitude is E = q/(4πε0r2). En is therefore constant over the entire surface area and can be take out of the integral. We then have
Φe = [q/(4πε0r2)]∫closed surfacedA = [q/(4πε0r2)]4πε0r2 = q/ε0.
The flux is proportional to the charge inside the surface and the proportional constant is 1/ε0.
Newton's laws (1st, 2nd, and 3rd law) describe the dynamics of physical systems. They describe how objects behave when forces act on them. They do not address the origin of the forces. Newton's law of gravitation states that any objects with mass exert forces on each other and it lets us calculate the direction and strength of the gravitational forces.
Maxwell's equations let us calculate the forces charged particles exert on each other. While Newton's laws only hold for particles moving with speeds much less than the speed of light, Maxwell's equations hold for particles moving with any speed. We say that Maxwell's equations are relativistically correct. Maxwell's equations are a set of four equations. The first of these equations is Gauss's Law.
Gauss' law states that the electric flux through any closed surface is equal to the total charge inside divided by ε0. Charges are the source and sinks of the electric field.
Using Coulomb's law, we have already shown that this is the case for a point charge at the center of a spherical surface. But Gauss' law holds for a closed surface of any shape and for any charge distribution inside that surface. Maxwell's equations are more general than Coulomb's law. Coulomb's law only holds for charges at rest, (or, approximately, for charges whose accelerations are small.) Coulomb's law can be derived from the first two of Maxwell's equations for static situations, i.e. when all charges are at rest or moving with uniform velocity.
The first two of Maxwell's equations let us calculate the electric field (magnitude and direction) due to any static charge distribution. Once we know the field then we know the force that this charge distribution exerts on another charge. If a charge distribution has a high degree of symmetry, then Gauss' law alone can be used to determine the magnitude of the electric field. The direction must be deduced from the symmetry of the situation.
Electric field for a uniform sphere of charge
Imagine a sphere of radius R with charge Q uniformly distributed inside. The symmetry of the charge distribution requires a spherically symmetric electric field. The field must either point radially inward toward the center or outward from the center of the sphere. (If we have a spherically symmetric charge distribution, then, no matter how we orient our coordinate system, the distribution always looks the same. The field must therefore also must look the same, no matter how we orient our coordinate system. A field that is not radial will look different if we rotate our coordinate system, i.e. if we look at it from another angle.) For a spherical symmetric charge distribution, the magnitude of E can therefore only depend on the radial coordinate r and on the charge Q. To determine E as a function of r, we use Gauss' law. We draw a spherical Gaussian surface of radius r centered at the center of the spherical charge distribution. The radius r of the surface can be larger or smaller than the radius R of the distribution.
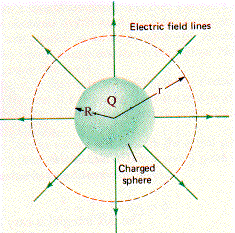 (i) Let r be greater than R, so that the surface encloses the entire
charge distribution.
(i) Let r be greater than R, so that the surface encloses the entire
charge distribution.
The electric field is radial, the vector E is
normal to any surface element dA. Thus
ΦE
= E 4πr2
= Qinside/ε0 = Q/ε0
from Gauss' law. We therefore have
E = Q/(4πε0r2)n.
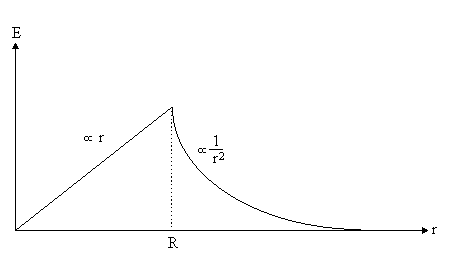
The field outside a uniformly distributed spherically symmetric charge distribution looks
like the field of a point charge. If Q is positive, the field points
outward, and if Q is negative, it points inward. Qinside can be written as the charge density
ρ = Q/V times
the volume of the charged sphere V = 4πR3/3. We can therefore
also write
E = ρR3/(3ε0r2)n.
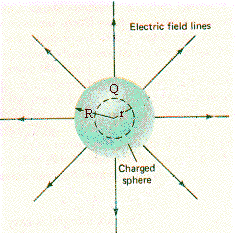 (ii)
Let r be smaller than R, so that the surface only encloses a part of the
charge distribution. Now Qinside is the charge density
ρ = Q/V times the volume
4πr3/3 of the distribution which lies inside the spherical
Gaussian surface. We therefore have
(ii)
Let r be smaller than R, so that the surface only encloses a part of the
charge distribution. Now Qinside is the charge density
ρ = Q/V times the volume
4πr3/3 of the distribution which lies inside the spherical
Gaussian surface. We therefore have
E = ρr/(3ε0)n.
The field inside the uniformly distributed spherically symmetric charge distribution increases linearly with r. Its direction is outward for a positive distribution, and inward for a
negative distribution.
Electric field near an infinite plane of charge
 For an infinite plane of charge lying in the x-y plane, with its normal
parallel to the z-axis, the field cannot depend on x or y. (If we shift the
origin of our coordinate system along the x- or y-axis, or rotate our
coordinate system about the z-axis, the charge distribution looks the same. The field must therefore also look the same.) The field must therefore be
parallel to the z-axis. The field must also be symmetric under reflection
about the x-y plane. This means that the field must have the same magnitude
at +z as it has at -z, but that it must point in opposite directions at +z
and at -z.
For an infinite plane of charge lying in the x-y plane, with its normal
parallel to the z-axis, the field cannot depend on x or y. (If we shift the
origin of our coordinate system along the x- or y-axis, or rotate our
coordinate system about the z-axis, the charge distribution looks the same. The field must therefore also look the same.) The field must therefore be
parallel to the z-axis. The field must also be symmetric under reflection
about the x-y plane. This means that the field must have the same magnitude
at +z as it has at -z, but that it must point in opposite directions at +z
and at -z.
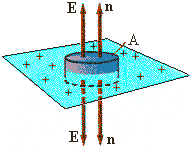
For our Gaussian surface we can choose a simple right circular cylinder
with faces parallel to the plane of charge. The field lines are parallel to
the sides of the cylinder, so the sides do not contribute to the flux.
The flux through the top surface is EA and the flux through the bottom surface is
EA. (On the top, both E and n
point upward, and on the bottom both E and n
point downward.)
Gauss' law yields
ΦE net = 2EA = Qinside/ε0.
If the surface charge density is σ, the Qinside = σA, and
ΦE nett
= 2EA = σA/ε0, and
E = σ/2ε0.
The field of an infinite planar charge distribution is uniform. It does
not decrease with distance. Of course, there are no infinite sheets of
charge. But our result is a good approximation to the field near a
finite-size plane of charge, as long as the dimensions of the plane are much
larger than the distance away from the plane where we want to know the
field.
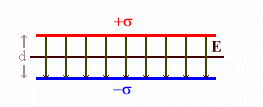 The most important application of the above result is
the superposition of the fields from two planar charge distributions which are
separated by some distance d. Place a uniformly charged plane with charge
density σ at x = +d/2 and a similar plane with charge density -σ at x = -d/2. The field due to the upper plane of charge is
The most important application of the above result is
the superposition of the fields from two planar charge distributions which are
separated by some distance d. Place a uniformly charged plane with charge
density σ at x = +d/2 and a similar plane with charge density -σ at x = -d/2. The field due to the upper plane of charge is
E1 = σ/2ε0, x > d/2, E1 =
-σ/2ε0, x < d/2.
The field due to the lower plane of charge is
E2 = σ/2ε0, x < -d/2, E2 =
-σ/2ε0, x > -d/2.
The total field in the region x < -d/2 is E = E1 + E2
= -σ/2ε0 + σ/2ε0 = 0.
Similarly, the total field in the region
x > d/2 is zero.
In the region between -d/2 and +d/2 the total field is is
E = E1 + E2 = -σ/2ε0 - σ/2ε0
= -σ/ε0.
The fields add to yield a uniform field between the planes, but they
precisely cancel outside the planes to give zero net field outside. Between the
planes the field points from the positive towards the negative plane. This is
the common configuration of a parallel plate
capacitor.
A sphere of radius R = 40 cm has a total positive charge of 26 microC
uniformly distributed over its surface. Calculate the magnitude of the electric field at
(a) 0 cm,
(b) 30 cm, and
(c) 60 cm from the center of the sphere.
Solution: