Vectors and vector fields
In physics, quantitative models are developed on the basis of measurements.
Measurements are made in standard increments, called units. Without units,
a measurement is meaningless. Many quantities are specified by a magnitude
(a number and the appropriate unit) and a direction in space. Such
quantities are called vector quantities. Symbols that denote these vector
quantities are bold letters, or normal letters with arrows drawn above.
Examples of vector quantities:
| displacement (d): |
d = 10 m north |
| velocity (v): |
v = 3 m/s eastward |
| acceleration (a) |
a = 6 m/s2 west |
| force (F) |
F = 9 N up |
To find the electric and magnetic fields produced by charged
particles and the electric and magnetic forces acting on objects, we have to
perform vector operations.
External link:
Vectors
- Fundamentals and Operations
Representing vectors
To uniquely specify vector quantities we need a reference point and
reference lines, i.e. we need a coordinate system. The most
commonly used coordinate systems are rectangular, Cartesian coordinate systems.
Other widely used coordinate systems are cylindrical and spherical coordinate
systems.
In Cartesian coordinates a vector is represented by its components
along the axes of the coordinate system.
Example: F = (Fx,
Fy) = Fxi + Fyj = 3 N i
- 4 N j.
Here i and j are unit vectors. Unit
vectors have magnitude 1 and no units. They are used as direction
indicators.
(i, j, k point in the x-, y-, and
z-direction, respectively.)
In the polar coordinates, in two
dimensions, a vector is represented by its magnitude and the angle its direction
makes with the x-axis.
Example: F = (F, φ) = (5 N, 306.87o)
= (5 N, -53.13o)
Cylindrical coordinates and spherical coordinates
are two different extensions of polar coordinates to three dimensions.
Adding and subtraction vectors
To add or subtract physical vectors, they have to have the same units.
To find the sum of two physical vector quantities with the same units algebraically, we add the x, y, and z-components of the individual vectors.
Example:
In two dimensions, let vector A have components (3, 4) and vector
B have
components (2, -3). Let C = A +
B be the sum of the two
vectors. Then the components of C are (3+2, 4+(-3) = (5, 1).
The magnitude of the vector C is C = (25 + 1)½ = 5.1,
and the angle C makes with the x-axis is φ = tan-1(1/5) =
0.197 rad = 11.3o.
To subtract vector B from vector
A we subtract the components
of vector B from the components of vector A.
Multiplying vectors
Vectors can be multiplied by a scalar (or number). Multiplying a
vector by a scalar changes the magnitude of the vector, but leaves its direction
unchanged.
Example:
F = (3 N, -4 N), 3F =
3*(3 N, -4 N) = (9 N, -12 N),
or
F = (F, φ) = (5 N, 323.13o),
3F = (15 N, 323.13o).
A vector can also be multiplied by another vector. There are two
different products of vectors.
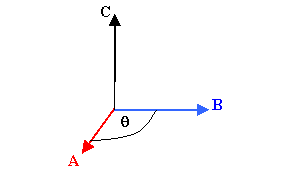
The scalar product or
dot
product of two vectors A and B is a scalar quantity (a number
with units) equal to the product of the magnitudes of the two vectors and the
cosine of the smallest angle between them.
A∙B = ABcosθ.
In terms
of the Cartesian components of the vectors A and B the scalar
product is written as
A∙B = AxBx + AyBy
+ AzBz.
In one dimension, the scalar product is
positive if the two vectors are parallel to each other, and it is negative if
the two vectors are anti-parallel to each other, i.e. if they point in opposite
directions.
 The
vector product or cross product of two vectors
A and B is defined
as the vector C = A × B.
The
vector product or cross product of two vectors
A and B is defined
as the vector C = A × B.
The magnitude of C
is C = AB sinθ, where θ is the smallest angle between the directions of the
vectors A and B.
C is perpendicular to both A and B, i.e. it is
perpendicular to the plane that contains both A and B.
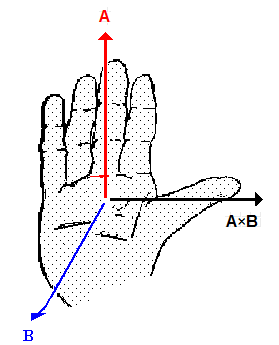
The
direction of C can be found by using the right-hand rule.
Let the
fingers of your right hand point in the direction of A.
Orient the
palm of your hand so that, as you curl your fingers, you can sweep them over to
point in the direction of B.
Your thumb points in the direction of
C = A × B.
 If A
and B are parallel or anti-parallel to each other, then C = A
× B = 0, since sinθ = 0.
If A
and B are parallel or anti-parallel to each other, then C = A
× B = 0, since sinθ = 0.
If A and B are perpendicular to
each other, then sinθ = 1 and C has its maximum possible magnitude.
Please click on the image below for an animation!
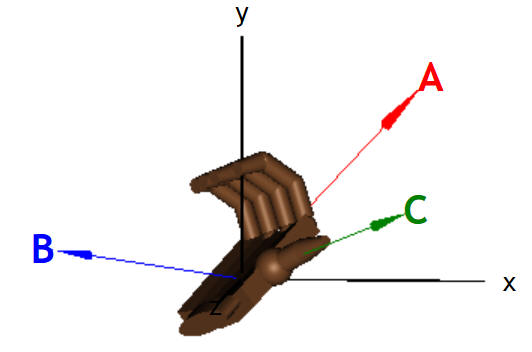
We can also find the Cartesian components of C = A × B in terms of
the components of A and B.
Cx = AyBz - AzBy
Cy = AzBx - AxBz
Cz
= AxBy - AyBx
Vector fields
If a vector can be assigned to each point in a subset of space, we have a
vector field.
The velocity of a fluid, for example the velocity of water flowing through a
pipe or down a drain, is a vector field. The velocity field describes the
motion of a fluid at every point. The length of the flow velocity vector
at any point is the flow speed.
The gravitational field
Forces are vectors. A force that we are familiar with is gravity. The gravitational force is not a
contact force. It acts at a distance. We introduce the concept of
the gravitational field to explain this action at a distance. Massive particles attract each
other. We say that massive particles produce gravitational fields and are
acted on by gravitational fields. The magnitude of the gravitational field
produced by a massive object at a point P is the gravitational force per
unit mass it exerts on another massive object located at that point.
The direction of the gravitational field is the direction of that force.
The gravitational field produced by a point mass always points towards the point
mass and decreases proportional to the inverse square of the distance from the
point mass. Near the surface of Earth the gravitational field produced by
Earth is nearly constant and has magnitude F/m = g = 9.8 m/s2. Its
direction is downward.
To find the total gravitational field at a point
calculate the vector sum of the gravitational fields produced by all masses that
do not produce negligibly small gravitational fields at that point.
The electric field
All charged particles interact via the Coulomb force. The Coulomb force is not
a contact force. It acts at a distance. We introduce the concept of the electric field to explain this action at a distance. We
say that charged particle produce electric fields and are acted on by electric
fields. The magnitude of the electric field E produced by a charged particle at a
point P is the electric force per unit positive charge it exerts on
another charged particle located at that point. The direction of the
electric field is the direction of that force on a positive charge. The
actual force on a particle with charge q is given by F = qE.
It points in the opposite direction of the electric field E for a
negative charge.
The electric field produce by a positive point charge always
points away from the point charge and the electric field produce by a negative
point charge always points towards the point charge. The electric field
decreases proportional to the inverse square of the distance from the point
charge. To find the total electrical field at a point calculate the
vector sum of the electric fields produced by all charges that do not
produce negligibly small electric fields at that point.
Graphical representations of vector fields
One way to graphically represent a vector field in two dimensions is by
drawing arrows an a grid. Set up a grid and find the magnitude and
direction of the field vector at every grid point. At each grid point draw
an arrow with the tail anchored at the grid point and a length proportional to
the magnitude of the vector in the direction of the field vector.
Examples:
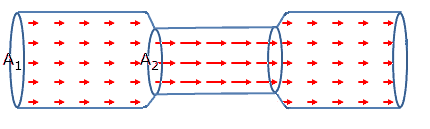 Velocity
field of an ideal fluid in a pipe
Velocity
field of an ideal fluid in a pipe
Continuity equation: A1v1
= A2v2
A2 = ½A1 --> v2
= 2v1
The arrows in the narrower section of the pipe
are twice
as long as the arrows in the wider section.
 Gravitational
field near the surface of Earth
Gravitational
field near the surface of Earth
g = 9.8 m/s2 = constant,
pointing downward.
All arrows have the same length.
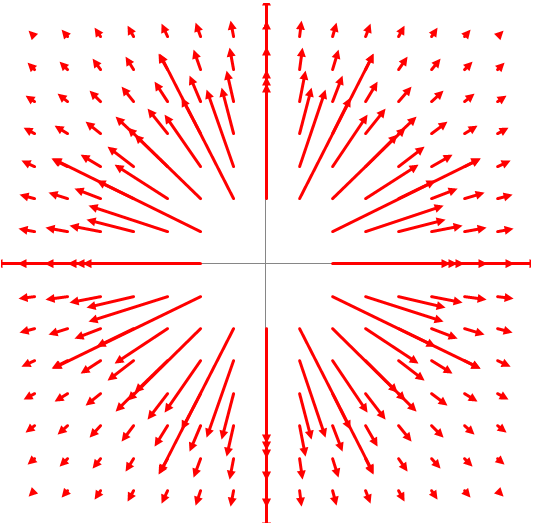 Electric
field of a positive point charge at the origin
Electric
field of a positive point charge at the origin
Note how fast the field
decreases as a function of the distance
from the point charge as a
consequence of the 1/r2 dependence.
Arrows near the origin are not
drawn, because they are too long.
The magnitude of the field approaches
infinity as we approach
the origin.
The arrow representation for the field produced by more than one source can
become quite messy. Another way to graphically represent a vector field is
by drawing field lines. The direction of the field at any point is
given by the direction of a line tangent to the field line, while the magnitude
of the field is given qualitatively by the density of field lines. Field
lines can emerge from sources and end in sinks, or they can form closed loops.
To draw a field line calculate the field at a point.
Draw a short
line segment (Δl --> 0) in the direction of the field.
Recalculate the field at the end of the line segment.
Repeat.
Examples:
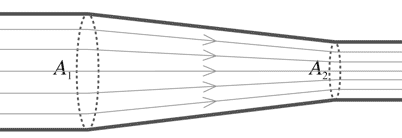 Velocity field lines or streamlines for a liquid flowing in a pipe.
Velocity field lines or streamlines for a liquid flowing in a pipe.
The density is
higher in region 2 where the velocity of the liquid has a greater magnitude.
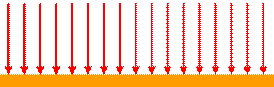
Field lines of the gravitational field near the surface of Earth. The lines are evenly
spaced since the field is constant.
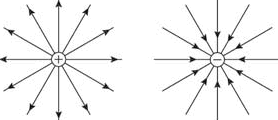
Electric field lines for a positive (source) and for a negative charge (sink).
The number of lines emerging from or converging at the charge is proportional to
the magnitude of the charge.
 The
vector product or cross product of two vectors
A and B is defined
as the vector C = A × B.
The
vector product or cross product of two vectors
A and B is defined
as the vector C = A × B.  If A
and B are parallel or anti-parallel to each other, then C = A
× B = 0, since sinθ = 0.
If A
and B are parallel or anti-parallel to each other, then C = A
× B = 0, since sinθ = 0.
 Velocity
field of an ideal fluid in a pipe
Velocity
field of an ideal fluid in a pipe Gravitational
field near the surface of Earth
Gravitational
field near the surface of Earth Electric
field of a positive point charge at the origin
Electric
field of a positive point charge at the origin Velocity field lines or streamlines for a liquid flowing in a pipe.
Velocity field lines or streamlines for a liquid flowing in a pipe.
