Materials can be classified according to the ease with which electrons can freely move through the material.  In some materials the outer electrons are firmly bound to their respective nuclei.  They can be pulled more towards one or the other side of the nucleus they are bound to, but they cannot leave it.  Those materials are called insulators.  In other materials the outermost electrons are free to move through the material.  They cannot easily leave the material but can move freely from atom to atom.  Those materials are called conductors.  Some materials are insulators at low temperatures, but become conductors as the temperature is raised.  The number of electrons that can freely move through the material increases with temperature.  Those materials are called semiconductors.

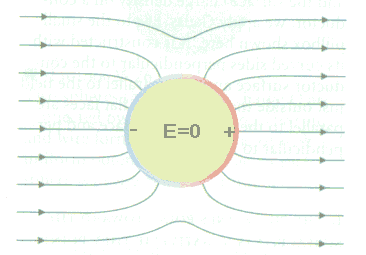
In a conductor electrons are free to move.  If they are acted on by a force, they will accelerate in the direction of the force.  If a conductor is placed into an external electric field, a force F = -eE acts on each free electron.  Electrons accelerate and gain velocity in a direction opposite to the field.  Soon electrons will pile up on the surface on one side of the conductor, while the surface on the other side will be depleted of electrons and have a net positive charge.  These separated negative and positive charges on opposing sides of the conductor produce their own electric field, which opposes the external field inside the conductor and modifies the field outside.

When enough electrons have piled up on one side and enough positive charge has been left on the other side, then the field produced by these separated charges exactly cancels the external field inside the conductor, and electrons inside the conductor no longer experience a force.  This is the case in the picture shown above.  The inside of the conducting sphere is field-free, while the previously constant external field outside has been modified.

In static equilibrium the inside of a conductor is field free.  If it were not, electrons would move and distribute themselves, so as to cancel out the field.  The inside of a conductor cannot contain any net charge.  Such charges would produce a field inside the conductor, and electrons would move and cancel out the field and neutralize the charge.  Any excess charge on a conductor must therefore reside on the surface.  The field just outside the conductor at the surface must be perpendicular to the surface.  If it were not, electrons would redistribute themselves to cancel out the field.  The strength of the electric field on the surface of a conductor can be found by applying Gauss' law.

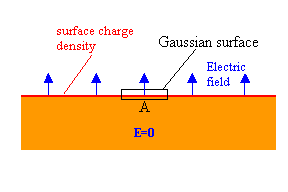The electric flux through the surface shown in the figure is Φ = Q_inside/ε₀ = σA/ε₀, where σ is the surface charge density and A is the area of the conductor's surface inside the Gaussian surface shown.  The flux through the sides of the Gaussian surface is zero, since E is perpendicular to the surface of the conductor.  The flux through the bottom of the Gaussian surface is zero since the electric field inside a conductor is zero.  The total flux through the Gaussian surface therefore equals the flux through the top, and we have Φ = EA.  We therefore have for the strength of the electric field near the surface of a conductor

E = σ/ε₀.

The surface of any conductor is an equipotential surface.  The field is everywhere perpendicular to the surface.  No work is being done moving a charge along on the surface.  The surface of a spherical conductor with radius R, carrying a charge Q is at a potential V = k_eQ/R.  If we have two spherical conductors with radii R₁ and R₂, respectively, at the same potential V, they carry charges Q₁ = R₁V/k and Q₂ = R₂V/k, respectively.  The electric fields near their surfaces are E₁ = k_eQ₁/R₁² = V/R₁ and E₂ = k_eQ₂/R₂² = V/R₂ respectively.  The smaller the radius, the larger is the electric field.

Near the surface of a charged conductor, the field is largest in places with the smallest local radius of curvature.

Very strong fields are found near sharp conducting tips.  Air molecules will be stripped of electrons if the field becomes too large (~3*10⁶ V/m).  The free electrons accelerate and collide with other molecules to make more ions and electrons.  A plasma forms between the conductor and the ground and the conductor discharges.  This is called a corona discharge.

A device that makes use of the strong field near a tip is the field ion microscope.  The field ion microscope has a sharp tip with a local radius of curvature of ~10 - 100 nm.  This tip faces a phosphor screen.  Under vacuum, a potential difference is established between the tip and the screen.  The tip is held at the more positive potential.  A small amount of inert gas is admitted, and gas atoms near the tip are ionized.  Electrons are ripped off these atoms.  The positively charged ions are accelerated by the intense electric field along a straight line toward the phosphor screen, where they are detected by converting their kinetic energy into light.  Each point on the tip maps into a different point on the screen, so that a magnified, image of the tip can be viewed.  Since the tip is only 10 - 100 nm in radius, one can achieve atomic resolution.  A typical field ion microscope image of a 'single crystal' tungsten tip is shown below.

The bright spots correspond to positions on the tip where the electric field is particularly high, i.e. where the local radius of curvature is particularly small.  This happens near atoms, so the microscope images the position of atoms in the tip.

In electrostatic equilibrium a conductor has the following properties.

• Any excess charge resides on the surface of the conductor.
• The electric field is zero within the solid part of the conductor.
• The electric field at the surface of a charged conductor is perpendicular to the surface.
• Charge accumulates, and the field is strongest, on pointy parts of the conductor.

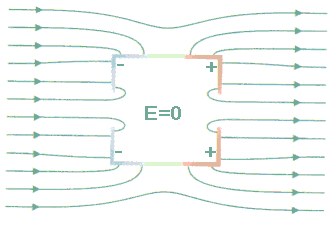The entire conductor is at the same potential.  There is no field inside the conductor.  A cavity inside a conductor, completely surrounded by conducting material, also is free of electric fields, if it does not contain any net charge itself.  A conductor shields its interior from any outside electric fields.  A charge located within a cavity in a conductor at equilibrium feels no force from charges outside the conductor.  Even if there are holes in the surface, the electric field does not penetrate very far.  A rule of thumb is that the electric field falls to zero over a distance approximately equal to the diameter of the hole.

In the diagram on the right, the field only penetrates a small distance through the holes into the box with conducting walls.

Think about:

Why are you safest inside your car during a thunderstorm?

Problem:

A square plate of copper with 50 cm sides has no net charge and is placed in a region of uniform electric field of 80 kN/C directed perpendicular to the plate.  Find
(a)  the charge density on each face of the plate and
(b)  the total charge on each phase. 

Solution:

• Reasoning:
  The surface charges on the plate must produce a field, which exactly cancels the external field inside the conductor.  The magnitude of the field produce by a surface charge is E_surface = σ/2ε₀.  We require that the field produced by the charges on the upper and the field produced by the charges on the lower surface together cancel the external field.  The charge density on one of the surfaces is positive.  On the other surface the charge density is negative it has the same magnitude, since the net charge is zero.  Inside the conductor the fields produced by the charges on the two surfaces have the same direction and we add their magnitudes to find the magnitude of the total field.  We need E_ext = 2E_surface = σ/ε₀.
• Details of the calculation:
  (a)  We need σ = ε₀*E_ext = ε₀*80 kN/C = 7*10^-7 C/m² for the magnitude of the charge density.  One plate has positive, and on plate has negative charge density.
  (b)  The magnitude of total charge on each plate is Q = σA = (7*10^-7 C/m²)*0.25 m² = 1.77*10^-7 C.  One plate has positive and one plate has negative charge.