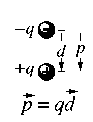 A system consisting of positive and a negative charge of equal magnitude q,
separated by a distance d is called an electric dipole. For an electric
dipole we define a new vector, called the electric dipole moment.
The magnitude of the dipole moment vector p is the magnitude of the charge
q times the distance d between them, p = qd. The vector points from the
negative towards the positive charge.
A system consisting of positive and a negative charge of equal magnitude q,
separated by a distance d is called an electric dipole. For an electric
dipole we define a new vector, called the electric dipole moment.
The magnitude of the dipole moment vector p is the magnitude of the charge
q times the distance d between them, p = qd. The vector points from the
negative towards the positive charge.
The dipole moment is a useful concept when effects of
microscopic charge separation are observable, but the actual distance
between the charges is too small to be measured. Molecules can
have permanent dipole moments and atoms and molecules without a
permanent dipole moment can acquire one when placed in an external
electric field.
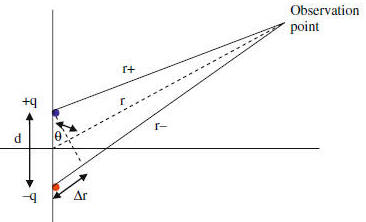 The
potential produced by an electric dipole is calculated summing the
potential of the two point charges that produce it. For a
point r whose distance from the negative charge is r- and
from the positive charge is r+ we have
The
potential produced by an electric dipole is calculated summing the
potential of the two point charges that produce it. For a
point r whose distance from the negative charge is r- and
from the positive charge is r+ we have
V(r) = kq[1/r+ - 1/r-]
= kq(r- - r+)/(r+r-).
If a the negative charge is placed on the z-axis at z = -d/2 and the
positive charge is placed on the z-axis at z = +d/2 then for large r
this becomes
V(r) = k q d cosθ/r2 = k p cosθ/r2,
where r- - r+ = ∆r = d cosθ, and 1/(r+r-)
is nearly equal to 1/r2. since r >> ∆r.
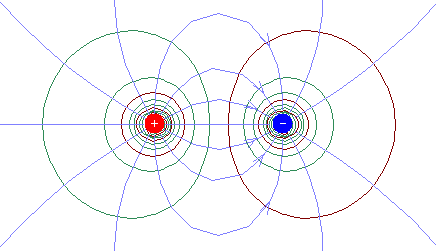 The dipole potential does not have spherical symmetry
and decreases as 1/distance2, much faster than the Coulomb
potential, which decreases as 1/distance. The dipole field
decreases as 1/distance3, and dipole effects become quickly
negligible as the distance increases. The figure to the right
shows the equipotential lines and field lines of an electric dipole in 2
dimensions as a cut through the 3-dimensional surfaces.
The dipole potential does not have spherical symmetry
and decreases as 1/distance2, much faster than the Coulomb
potential, which decreases as 1/distance. The dipole field
decreases as 1/distance3, and dipole effects become quickly
negligible as the distance increases. The figure to the right
shows the equipotential lines and field lines of an electric dipole in 2
dimensions as a cut through the 3-dimensional surfaces.
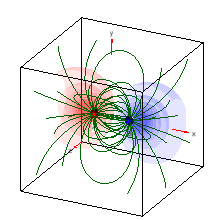
Please also explore this
3-dimensional representation below.
Please click on the image!
In a uniform electric field the net force on an electric
dipole is zero.
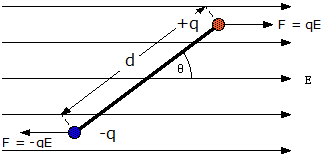 The negative and
the positive charge are acted on by forces that have the same magnitude but
opposite directions. But if the dipole moment p is not aligned with the
electric field, then a torque acts on the dipole, trying to align
p
with E.
The negative and
the positive charge are acted on by forces that have the same magnitude but
opposite directions. But if the dipole moment p is not aligned with the
electric field, then a torque acts on the dipole, trying to align
p
with E.
The magnitude of this torque if τ = pE sinθ.
To rotate the dipole away from alignment, you have to
apply an external torque and do work. The work done by this
external torque is stored as potential energy and can be converted into
other forms of energy. The potential energy of a dipole in an
external field is
Udipole = -pE cosθ.
The potential energy is lowest when the dipole is
aligned with E and highest if it is anti-aligned.
If the field is not uniform, then the magnitude of the electric force
acting on the positive charge can be different from that acting on the
negative charge, and there can be a net force acting on the dipole.
Why do we care about dipoles?
Many neutral molecules have permanent dipole moments and others can have
induced dipole moments due to polarization. Electric dipole interactions
are much weaker than the Coulomb interaction between charged particles.
Collectively they are called
van
der Waals forces.
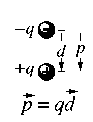 A system consisting of positive and a negative charge of equal magnitude q,
separated by a distance d is called an electric dipole. For an electric
dipole we define a new vector, called the electric dipole moment.
The magnitude of the dipole moment vector p is the magnitude of the charge
q times the distance d between them, p = qd. The vector points from the
negative towards the positive charge.
A system consisting of positive and a negative charge of equal magnitude q,
separated by a distance d is called an electric dipole. For an electric
dipole we define a new vector, called the electric dipole moment.
The magnitude of the dipole moment vector p is the magnitude of the charge
q times the distance d between them, p = qd. The vector points from the
negative towards the positive charge. The
potential produced by an electric dipole is calculated summing the
potential of the two point charges that produce it. For a
point r whose distance from the negative charge is r- and
from the positive charge is r+ we have
The
potential produced by an electric dipole is calculated summing the
potential of the two point charges that produce it. For a
point r whose distance from the negative charge is r- and
from the positive charge is r+ we have The dipole potential does not have spherical symmetry
and decreases as 1/distance2, much faster than the Coulomb
potential, which decreases as 1/distance. The dipole field
decreases as 1/distance3, and dipole effects become quickly
negligible as the distance increases. The figure to the right
shows the equipotential lines and field lines of an electric dipole in 2
dimensions as a cut through the 3-dimensional surfaces.
The dipole potential does not have spherical symmetry
and decreases as 1/distance2, much faster than the Coulomb
potential, which decreases as 1/distance. The dipole field
decreases as 1/distance3, and dipole effects become quickly
negligible as the distance increases. The figure to the right
shows the equipotential lines and field lines of an electric dipole in 2
dimensions as a cut through the 3-dimensional surfaces.
 The negative and
the positive charge are acted on by forces that have the same magnitude but
opposite directions. But if the dipole moment p is not aligned with the
electric field, then a torque acts on the dipole, trying to align
p
with E.
The negative and
the positive charge are acted on by forces that have the same magnitude but
opposite directions. But if the dipole moment p is not aligned with the
electric field, then a torque acts on the dipole, trying to align
p
with E.