Resistors in series and parallel

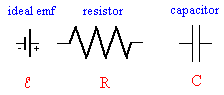The circuit elements we have considered thus far are the emf (power supply or battery), the resistor (any device that converts electrical energy into thermal energy), and the capacitor (a device for storing separated charges).  In circuit diagrams they are represented by the symbols shown on the right.

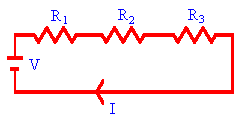Most interesting circuits consist of more than just one emf and one resistor.  Some circuits have more than one resistor connected in series, as shown in the figure on the right.  In such a circuit the same current I flows through each resistor.  The potential difference across resistor 1 is V₁ = IR₁, the potential difference across resistor 2 is V₂ = IR₂, and the potential difference across resistor 3 is V₃ = IR₃.  The potential difference across the chain is equal to the battery voltage V.  We have V = V₁ + V₂ + V₃ = IR₁ + IR₂ + IR₃.  The equivalent resistance of the circuit can be calculated from V = IR.  The two equation yield

R = R₁ + R₂ + R₃.

The equivalent resistance of any number of resistors connected in series is the sum of their individual resistances.
It is always greater than any of the individual resistances.

Example:

In the figure above, let R₁ = 4 Ω, R₂ = 4 Ω, and R₃ = 12 Ω.  Then the equivalent resistance is R = 20 Ω. 
If the battery voltage is 10 V, then the current in the circuit is I = V/R = (10 V)/(20 Ω) = 0.5 A. 
The current through each resistor is 0.5 A.  The power dissipated is P = IV = 5 W.
Assume another 20 Ω resistor is added to the chain.  Adding another 20 Ω resistor increases the equivalent resistance to R = 40 Ω.  The current drops to I = (10 V)/(40 Ω) = 0.25 A.  The power dissipated drops to P = 2.5 W.

Adding an additional resistance in series

• reduces the current in the circuit,
• reduces the power I²R_i dissipated by each of the i resistances R_i,
• reduces the total power dissipated.

The light bulbs in a chain of Christmas lights are often connected in series.  If 10 identical light bulbs are in the chain and the voltage across the chain is 120V, then the voltage across each bulb is 12 V.  The same current flows through each bulb.  If one bulb burns out, no current flows, and none of the bulbs will light up.

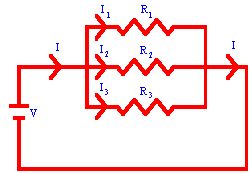It is more common to have more than one resistance connected in parallel, as shown in the figure to the right.  The current I from the battery is divided into I₁, I₂, and I₃ flowing through R₁, R₂, and R₃, respectively.  These three currents recombine when the branches meet again.
I = I₁ + I₂ + I₃.
The voltage across each resistor in the parallel circuit shown is equal to the battery voltage V.
We have I₁ = V/R₁, I₂ = V/R₂, I₃ = V/R₃.  We find the equivalent resistance from V = IR,
1/R = I/V = (I₁ + I₂ + I₃)/V = (1/R₁) + (1/R₂) + (1/R₃).

1/R = (1/R₁) + (1/R₂) + (1/R₃).

For a set of parallel resistors the reciprocal of their equivalent resistance equals the sum of the reciprocals of their individual resistances.
Note: The equivalent resistance of any parallel combination of resistors is always less than any of the individual resistances.

Example:

Assume that in the circuit shown on the right R₁ = 8 Ω, R₂ = 8 Ω, and R₃ = 4 Ω.
Then 1/R = 1/(8 Ω) + 1/(8 Ω) + 1/(4 Ω) = 1/(2 Ω).  R = 2 Ω.
If the battery voltage is 10 V, then the current in the circuit is I = V/R = (10 V)/(2 Ω) = 5 A.
The individual currents are found from I_i = V/R_i.  The voltage across each resistor is 10 V, therefore
I₁ = (10 V)/(8 Ω) = 1.25 A,
I₂ = (10 V)/(8 Ω) = 1.25 A,
I₃ = (10 V)/(4 Ω) = 2.5 A.
The currents add to yield the total current I = 5 A.
If another 8 Ω resistor is added in parallel, a current of 1.25 A will flow through this resistor.  The total current in the circuit increases, the equivalent resistance decreases, and the power P = IV dissipated by the circuit increases.

If 10 Christmas lights are connected in parallel, then one burned-out bulb does not prevent the other bulbs from lighting up.  However, a different type of bulb must be used if the bulbs are to be connected parallel to a 120 V outlet, because the voltage across each bulb will be 120 V.

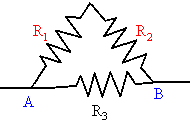Often circuits contain one emf and a number of series and parallel connections.  An example is the section of a circuit shown on the right.  The total resistance of such a circuit can be found by sequentially replacing parts of the circuit with a single equivalent resistance.  The equivalent circuit then consists of a single emf and a single resistor.  This procedure yields the total current flowing in the circuit, and the currents flowing through the individual resistors can be found by reversing the reduction process.

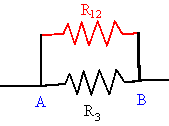Let us find the total resistance between the points A and B in the circuit to the right. 
R₁ and R₂ are in series and are replaced by R₁₂ = R₁ + R₂.
Now R₁₂ and R₃ are in parallel and can be replaced by R, where 1/R = 1/R₁₂ + 1/R₃.
If R₁ = R₂ = R₃ = 1 Ω, then R₁₂ = 2 Ω and R = (2/3) Ω. 
If a 6 V battery is connected across points A and B, then the current flowing in the circuit is I = V/R = 9 A. 
The current flowing through R₃ is I = V/R₃, the current flowing through R₁ and R₂ is V/R₁₂ = 3 A.

General rules for finding the equivalent resistance of a simple circuit:

• Two (or more) resistors with their heads directly connected together and their tails directly connected together are in parallel.  They can be replaced by one equivalent resistor R using 1/R = (1/R₁) + (1/R₂) + (1/R₃) + ....
• Two (or more) resistors connected together so that the tail of one is connected to the head of the next, with no other path for the current to take along the line connecting them, are in series.  They can be replaced by one equivalent resistor R using R = R₁ + R₂ + R₃+....
• For resistors in series, the same current flows through each resistor, and for resistors in parallel, the same voltage drops across each resistor.

Problem:

What are the largest and smallest resistances you can obtain by connecting a 36 Ω, a 50 Ω, and a 700 Ω resistor together?

Solution:

• Reasoning:
  To obtain the largest resistance, we have to connect the resistors in series.
  To obtain the smallest resistance, we have to connect the resistors in parallel.
• Details of the calculation:
  R_largest = (36 + 50 + 700) Ω = 786 Ω.
  1/R_smallest = (1/36 + 1/50 + 1/700) Ω^-1 = 0.0492/Ω.
  R_smallest = 20.32 Ω.

Embedded Question 2

What is the equivalent resistance between the points A and B?

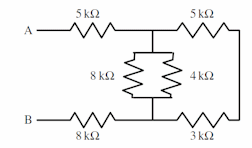
Discuss this with your fellow students in the discussion forum!
Discuss the rules for finding the equivalent resistance of multiple resistors in series and parallel.

Kirchhoff's rules

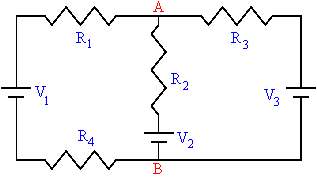A junction in a circuit is a point where at least three circuit paths meet.  A branch is a path connecting two junctions.  The circuit on the right has two junctions, labeled A and B, and three branches, namely the three different paths from A to B.  This circuit is a multi-loop circuit, with more than one battery in different branches of the circuit.  To analyze such a circuit and to find the currents in all branches of the multi-loop circuit one must use Kirchhoff's rules.

• Kirchhoff's first rule:
  Junction rule:
  At any junction point in a circuit where the current can divide, the sum of the currents into the junction must equal the sum of the currents out of the junction.  (This is a consequence of charge conservation.  "What flows in, has to flow out.")
• Kirchhoff's second rule:
  Loop rule:
  When any closed circuit loop is traversed, the algebraic sum of the changes in the potential must equal zero.  (This is a consequence of conservation of energy.  The electric force is a conservative force.  Once a reference point has been chosen, the potential depends only on the position.)

Kirchhoff's rules apply to all circuit.

General procedure for analyzing a circuit using Kirchhoff's rules:

• Replace any combination of resistors in series or parallel with their equivalent resistance.  Label each remaining resistor and each emf with a symbol.
• Choose a direction for the current in each branch of the circuit, and label each current.
• Add plus and minus signs to label the high and low potential sides of each circuit element, (i.e. each emf, resistor, capacitor).  Label the side of the resistor on which the current enters with a plus sign (+) and the side on which the current exits with a minus sign (-).
  • Sometimes it is hard to predict in which direction the current will flow in a particular loop.  Simply pick a direction.  If the real current flows in the opposite direction, the current in your solution will be negative.  The minus sign just indicates that the current flows in the direction opposite to the one you picked.
• Apply Kirchhoff's first rule to all but one of the junctions in the circuit.
  • Each time you use the junction rule a current that has not been used before must be included.
• Apply Kirchhoff's second rule to as many loops as needed to obtain as many equations (including the junction equations) as you have unknowns.
  • Each time you use the loop equation you have to include a circuit element that has not been used before.
  • To write down a loop equation, you choose a starting point, and then follow a path around the loop in one direction until you get back to the starting point.  As you cross a battery or a resistors note the change in voltage.  If you cross from - to +, the change is positive.  If you cross from + to -, the change is negative.  Add these changes in voltage and set the sum equal to zero.
• Solve the equations to obtain the values of the unknowns.

Example:

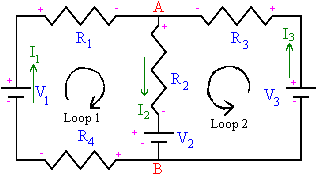In the circuit to the right, let V₁ be a 1 V battery, V₂ be a 2 V battery, V₃ be a 3 V  battery, and let each resistor be a 1 Ω resistor.  Pick directions for the currents as shown in the diagram.

• Junction A: I₁ + I₃ = I₂
• Loop 1: V₁ - I₁R₁ - I₂R₂ - V₂ - I₁R₄ = 0
  This yields
  1V - I₁1 Ω - I₂1 Ω - 2 V - I₁1 Ω = 0, or 2I₁ + I₂ = -1 A.  (Units: V/Ω = A)
• Loop 2: V₃ - I₃R₃ - I₂R₂ - V₂ = 0
  This yields
  3V - I₃1 Ω - I₂1 Ω - 2 V = 0, or I₃ + I₂ = 1 A.
• We now have to solve the three equations,
  I₁ + I₃ = I₂,
  2I₁ + I₂ = -1 A,
  I₃ + I₂ = 1 A,
  for the three unknown currents.
  • Eliminate I₃: I₃ = 1 A - I₂ using the third equation. The first two equations then yield
    I₁ + 1 A - I₂ = I₂, I ₁- 2I₂ = -1 A,
    2I₁ + I₂ = -1 A.
  • Eliminate I₂: I₂ = -1 A - 2I₁.  We now can solve for I₁.
    I₁ + 2 A + 4I₁ = -1 A, 5I₁ = -3 A, I₁ = -(3/5) A.
  • Now we can solve for I₂ and I₃.
    I₂ = -1 A - 2I₁ = -1 A + (6/5) A = (1/5) A
    I₃ = I₂ - I₁ = (4/5) A
• I₂ and I₃ flow in the directions picked in the diagram, I₁ flows in a direction opposite to the one picked in the diagram.