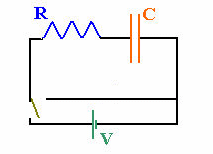
Resistors are simple circuit elements.  A constant current flows when a resistor is connected across the terminals of a battery.  If a capacitor is added to the circuit, the situation changes.  If a parallel-plate capacitor C is connected in series with a resistor R, and the two ends of the chain are connected to a battery as shown in the diagram to the right, then the battery will pump electrons from the plate connected to the negative terminal to the plate connected to the positive terminal.  The magnitude of the net charge on each plate will increase with time as

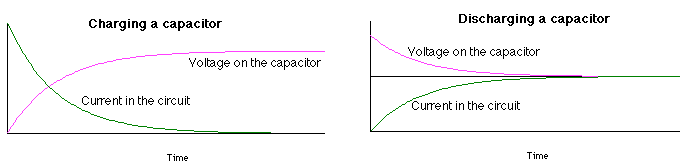
Q = Q₀(1 - e^-t/τ),

where τ = RC is the time constant of the RC (resistor-capacitor) circuit. 
At t = 0, Q = 0, and when t becomes very large compared to τ, then e^-t/τ << 0, and Q = Q₀ = CV₀. 
For the voltage across the capacitor we have V = Q/C, so

V = V₀(1 - e^-t/τ),

where V₀ is the battery voltage.
The current flowing in the circuit as the capacitor is being charged is

I = dQ/dt = I₀e^-t/τ = (V₀/R)e^-t/τ.

The time it takes to charge the capacitor so that it holds half of the maximum charge for a given voltage is t_½ = τ ln2. 
This is also the time it takes for the voltage across the capacitor to be equal to ½ of the battery voltage and the time it takes for the current to decrease to ½ of its maximum value.

If, after the capacitor has been fully charged, it is disconnected from the battery and the switch is closed, i.e, the RC circuit is shorted out, then the charge on the capacitor will decrease as Q = Q₀e^-t/τ, the voltage will decrease as V = V₀e^-t/τ, and the current flowing in the circuit will be I = ΔQ/Δt = -I₀e^-t/τ = -(V₀/R)e^-t/τ.  The minus sign indicates that the current that discharges the capacitor flows in the opposite direction as the current that charges the capacitor.

Problem:

The intermittent wiper system in a car is based on an RC time constant and utilizes a 0.40 μF capacitor.  What resistance R is needed for a 2 s time constant?

Solution:

• Reasoning:
  The time constant of an RC circuit is τ = RC. 
• Details of the calculation:
  R = τ/C = (2 s)/(4*10^-7) F = 5*10⁶ Ω = 5 MΩ.

Why do we care about RC circuit?

All real circuits have some capacitance.  Often we can model a real circuit as a chain of capacitors and resistors connected in series and parallel. The time constant of such a circuit characterizes the time it takes for the capacitors to charge and discharge and therefore limits the maximum speed with which signals can travel through the circuit.  In real circuits for example the full current does not flow the instant you flip a switch.  It takes some time to build up to its steady-state value.