Current density and current
Most electrical devices are not electrostatic devices. Most electrical
devices require the flow of a current. A current requires
moving charges.
Let ρ+ = n+q+
be the density of the positive charges in some region, i.e. the amount
of positive charge per unit volume, and let ρ- = n-q-
be the density
of the negative charges. Here n+ and n- are the number of positively and
negatively charged particles per unit volume and q+ and q-
are the charge of each positively and negatively charged particle,
respectively.
(n+ and n- are positive numbers q+ is a
positive number with units and q- is a negative number with
units. Therefore ρ+ is a positive number with units and ρ-
is a negative number with units.)
In neutral ordinary matter ρ+ + ρ-
= 0, i.e. the net charge per unit volume is zero.
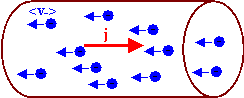The current density is
defined as j = ρ+<v+> + ρ-<v->.
In this expression <v+> and <v-> are the
average velocities of the positive and negative charges, respectively.
If <v-> = 0 and only positive charges are
moving, then the direction of the current density is the direction of
the velocity of the positive charges. In ordinary conductors the
positive charges have zero average velocity and only the negative
charges are moving. Then the direction of the current density is
opposite to the direction of the velocity of the negative charges, as
shown in the diagram on the right.
The SI unit of current density is (C/m3)(m/s) = C/(m2s).
The current density is a vector. Its magnitude is the net
amount of charge that crosses a unit area perpendicular to its direction
per second in the direction of j minus the net amount of charge
that crosses the same unit area per second opposite to the direction of
j. If just as many negative as positive charges move across
a unit area in the same direction per second, then the current density
is zero.
The electric current
I is the net amount of charge which flows through a surface, i.e. the
flux of the current density
through a surface area.
I = ∫j∙dA = dQ/dt.
If j is uniform across the surface and constant in time, then
I = j∙A = j*Aperpendicular =
ΔQ/Δt.
The SI unit of current is Ampere
= Coulomb/second (A = C/s). The current I is not a
vector. It is a scalar, but it can be a negative or positive
number. When obtaining the current from the current density using
I = j∙A,
we have to choose a direction for the unit vector n normal to the
surface area through which the current flows. If the net flow of positive charge is in the direction of
n, (or the net flow of negative charge is in a
direction opposite to the direction of n), then the
current I is positive. If the reverse is true, then the current I
is negative.
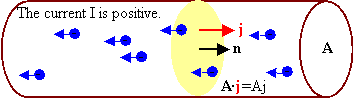Assume that a
steady current flows in a wire
with cross-sectional area A. The electrons move with constant
average velocity to the left as shown in the diagram. The
current density is a vector pointing towards the right. Let the
normal to the cross-sectional area point towards the right. Then I = j*A = ΔQ/Δt, and the current is a positive number.
(If the electrons were moving towards the right, then j would
point towards the left and I would be a negative number.)
The magnitude of the current I moving through a wire is given by
I = |ρ-|<v->A = n-|q-|<v->A
= -neqe<v->A,
where ne
is the number of free electrons per unit volume. The magnitude of the current I equals the
number of electrons that pass any point along the wire per second times the unit
of charge qe = 1.6*10-19 C. <v-> is the drift speed
of the electrons. It is their average speed, as they move along
the wire.
Currents are most often produced by the movement of electrons in conductors.
But the movement of ions can also produce a current.
External links:
Ionizing air with fire:
https://www.youtube.com/watch?v=PwzoLsAdrRA
MIT Physics Demo -- Conductivity of Ionized Water:
https://www.youtube.com/watch?v=Rf2mS4J0FNg
Problem:
In a storm, falling raindrops carry a current density of +1.0*10-5
A/m2 towards the ground. If 1000 drops strike each square meter
of ground per second, calculate the magnitude and sign of the average charge on
each raindrop in Coulomb.
Solution:
- Reasoning
The the current density is given. j = +1.0*10-5 A/m2 =
+1.0*10-5 C/(s m2), downward.
1000 drops per square meter carrying positive charge produce this current
density.
- Details of the calculation:
1.0*10-5 C/(s m2) = 1000 drops/(s m2) *
Q C/drop
Q = 10-8 C is the average charge on each raindrop.
What causes the electrons to move in a wire?
Particles accelerate when they acted on by
forces. When a particle with charge q is placed in an electric
field E, a force F = qE is
acting on the particle and it accelerates. To produce an electric field,
something has to do work and separate charges. Such a device is
called an emf.
Examples of an emf are a battery or a power supply. Such an emf
separates charges by moving electrons internally from its positive to
its negative terminal. This produces an electric field, which
points from the positive to the negative terminal outside and inside the
emf. Electrons in a wire placed in this electric field close to
the battery will accelerate toward the end of the wire closest to the
positive terminal. But if the wire is not connected to the
terminals of the emf, they will pile up at one end of the wire, leaving
net positive charge at the other end. The separated charges in the
wire then produce their own electric field opposing the field produced
by the emf. The interior of the wire will be field free and
charges will no longer accelerate.
If, however, the wire is
connected to the emf, then the emf can pump the electrons through its
interior back from the positive to the negative terminal. Then
field inside the wire will not be zero, and electrons will continue to
accelerate towards the positive terminal.
Steady currents can only flow in
continuous loops. At any point, just as much charge has to
flow out of a small volume surrounding the point as flows into the
volume. If this were not so, charge would accumulate at the point,
setting up its own electric field. This field would exert an
additional force on the moving charges, disrupting the steady current.
The electric field in a homogeneous wire with constant cross-sectional
area carrying a steady current is the same everywhere. If it were
not, electrons would move with different velocities in different
sections, and charges would accumulate in certain regions. The
field produced by these charges would disrupt the steady current.
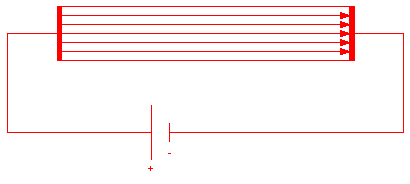
The diagram on the right shows the field in a wire carrying a steady
current.
Even though an electric force is continuously acting on each electrons in a
wire when a steady current is flowing, the electrons do not continue to
accelerate indefinitely, but reach an average terminal velocity, called the
drift velocity <v->.
When the electrons move with the drift velocity, then the resistive forces
(frictional forces) acting on them are equal in magnitude and opposite in
direction to the electric forces. Typical drift speeds are on the order of
1 mm/s.
The resistive forces depend on the type of material the wire is made of.
The terminal velocity depends on the electric force and the resistive force.
The higher the terminal velocity, the larger is the current. The current
will increase if the voltage across the wire increases, (this increases the
strength of the electric field), and decrease if the resistive forces increase
in strength. We write
I = ΔV/R, or R = ΔV/I.
This expression defines the resistance R
of the wire. The resistance is a measure of the resistive forces. The unit
of resistance is
Ohm = Volt/Ampere (Ω = V/A).
Summary:
-
Steady currents flow in continuous loops.
-
The emf does work separating charges and supplies voltage.
It raises the potential energy of the charges
This potential energy is converted to other forms of energy as charges move through the circuit and recombine, only to be separated again by the emf.
-
In resistors, the potential energy is converted into
thermal energy.
Problem:
An emf source of 6.0 V is connected to a purely resistive lamp and a current
of 2.0 A flows. All the wires are resistance-free. What is the
resistance of the lamp?
Solution:
- Reasoning:
The resistance is defined as the ratio ΔV/I.
- Details of the calculation:
R = ΔV/I = (6 V)/(2 A) = 3 Ω.
The resistivity ρ of a material is the
resistance of a piece of material with unit cross sectional area and unit
length. The resistance of a wire is proportional to its length l
and inverse proportional to its cross-sectional area A. We have
R = ρl/A.
The unit of resistivity is
Ωm. The conductivity
σ of a material is σ = 1/ρ.
External link:
Resistivity and Temperature Coefficient at 20o C of common materials
The resistivity is a property of the material a conductor is made of.
For many conductors it only weakly depends on the voltage ΔV across the
conductor or the current I flowing through the conductor over a wide range of
voltages and currents as long as the temperature of the material is held
constant. This is called Ohm's law.
R = ΔV/I is approximately constant for many conductors at constant temperature.
Ohm's law breaks down under extreme conditions for all
conductors. Many modern materials do not obey Ohms law under
any circumstances. (Such materials are called non-ohmic materials.)
The resistivity and therefore the resistance of most materials depends on the
temperature. Tables often list the resistivity at some reference
temperature T0, (for example at 20oC), and then list a
temperature coefficient α = (1/ρ0)Δρ/ΔT. To find the resistance
at some temperature T use ρ = ρ0[1 +α (T - T0)].
A thermistors is a semiconductor crystal whose resistance strongly depends on
temperature. Thermistor thermometers use thermistors to measure
temperature. The resistance is measured to obtain the temperature.
Thermistors are used as clinical temperature sensors in stethoscopes, as probes
during surgery, and in other medical devices where temperature detection and
control is vital.
Problem:
A annealed copper wire has a length of 160 m and a diameter of 1.00 mm. If the
wire is connected to a 1.5 V battery, how much current flows through the wire?
Solution:
- Reasoning:
The current can be found from Ohm's Law, V = IR. V is
the battery voltage, so if R can be determined, the current can be
calculated.
The resistance of the wire is R = ρl/A.
For
copper ρ = 1.72*10-8 Ωm.
- Details of the calculation:
The cross-sectional area of the wire
is A = πr2 = π(0.0005)2 = 7.85*0-7
m2.
The resistance of the wire then is ((1.72*10-8)*160/(7.85*10-7))Ω
= 3.5 Ω.
The current is I = V/R = (1.5/3.5)A = 0.428 A.
Problem:
An aluminum wire has a resistance of 0.10 Ω. If you draw this wire
through a die, making it thinner and twice as long, what will be its new
resistance?
Solution:
- Reasoning:
The initial resistance Ri of the aluminum wire
with length L and cross-sectional area A is equal to is Ri = ρl/A.
The initial volume of the wire is AL. After passing the wire through the
die, its length has changed to L' and its cross-sectional area is equal A'.
Its final volume is therefore equal to A'L'. Since the density of the
aluminum does not change, the volume of the wire does not change, and
therefore the initial and final dimensions of the wire are related by AL =
A'L'.
- Details of the calculation:
We have A' = L/L'A = A/2.
The final resistance Rf of
the wire is given by Rf = ρL'/A' = 4ρL/A = 4Ri
= 0.40 Ω.
Problem
A high voltage transmission line has an aluminum cable of diameter 3.0 cm, 200 km long.
What is the resistance of this cable?
Solution:
- Reasoning:
The resistivity of aluminum is 2.65*10-8 Ωm.
The length of the cable is 2*105 m.
The diameter of the cable is 3 cm and its cross-sectional area is equal to
π(d/2)2 or 7.1*10-4
m2. Substituting these values into R =
ρL/A the
resistance of the cable can be determined.
- Details of the calculation:
R = (2.65*10-8*2*105) Ω/( 7.1*10-4)
= 7.5 Ω.
Popular analogy
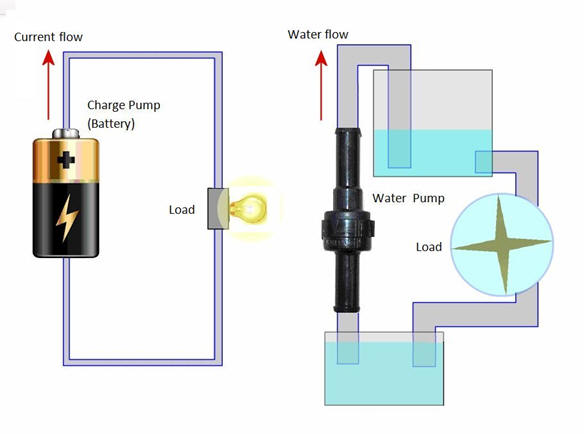
What is different?
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/watcir.html
Embedded Question 1
Which diagram below does not represent an electrical current?
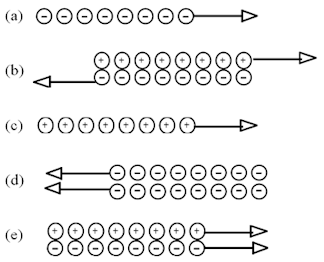
Discuss this with your fellow students in the discussion forum!
Discuss different ways one can produce a steady current.