The Hall effect

In 1879 Hall discovered a small electric field E_H in a conductor carrying a current I in a magnetic field B.  The electric field E_H is perpendicular to both the direction of the magnetic field and the direction of current flow.  Hall used this observation to prove that the current in metal conductors is carried by negative charges.

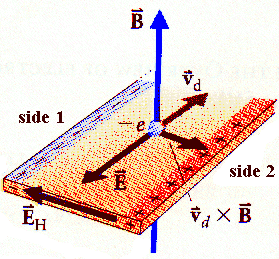The current in the metal strip shown  is flowing because a power supply establishes an electric field E in the strip.  The conduction electrons move with an average drift velocity v_d opposite to the direction of E.  In the uniform field B the magnetic force on each electron is F = -q_ev_d × B.  It causes the electrons to drift towards side 1 of the strip, leaving excess positive charge on side 2.  These separated charges produce the electric field E_H.  The electrons will stop drifting sideways, when the electric force -q_eE_H cancels the magnetic force -q_ev × B, or E_H = v_dB.  The resulting potential difference across the strip is

 E_HL = ΔV = V₂ - V₂ = v_dBL. 

This is known as the Hall potential.  If positive charges were moving in the strip, they would drift towards side 1 and the sign of the Hall potential would change

The Hall effect can be used to measure the strength of the magnetic field perpendicular to a current-carrying metal strip, called a Hall probe.  The dimensions of the probe and the drift velocity for a given power-supply voltage are known.  The potential difference ΔV then yields the magnetic field strength B_┴.

Problem:

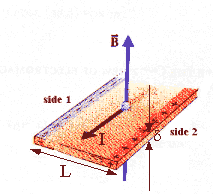A current I is flowing in the metal strip of width L and thickness δ as shown .  The metal  contains n_e free electrons per unit volume.  A magnetic field B penetrates the strip as shown.  In terms of I, B, n_e, and L, find the potential difference between side 1 and side 2.

Solution:

• Reasoning:
  The magnitude of the current I moving through a wire is given by
  I = |ρ_-|<v_->A = n_eq_ev_dA,
  where n_e is the number of free electrons per unit volume.  The current I equals the number of electrons that pass any point along the wire per second times the unit of charge q_e.  <v-> = v_d is the drift speed of the electrons.  It is their average speed, as they move along the wire.
  We have v_d = I/(n_eq_eA) = I/(n_eq_eLδ). 
  ∆V = v_dBL = IB/(n_eq_eδ).